无线电信号的高阶谱估计分析
2018-01-18肖军刘洲洲
肖军,刘洲洲
(西安航空学院电子工程学院,陕西西安710077)
随着无线电行业的迅速发展,无线电信号的频谱分析应用得到广泛应用。在语音信号辨别、分析雷达中含有的杂波信号、波达方向的估量、地震勘测信号的处理、水声信号的处理、非线性系统的识别、流体力学的内波分析等随机过程中有重要的应用价值[1,16]。随之产生的有无线电频谱感知、软件无线电和认知无线电等技术[2-5]。
同时,无线电信号在信道传输的过程中会受到各种因素的干扰,有来自外部的干扰噪声,如来自太阳的干扰;在信号的发射或接收过程中,因设备自身原因,也会有热噪声;传输信道中信号也存在衰落的问题,不同信道(如瑞利信道,莱斯信道和高斯白噪声信道等)对信号的影响不同。不同信号的传输频段间传输占用不同的频段,但相互之间仍可能干扰。同一信号的不同相邻码元之间也可能存在码间干扰。诸如此类的干扰对信号的接收和检测都有一定的挑战。
1 无线电传输模型的建立
把一个均值为零,功率谱密度是非零常数的平稳随机过程,且其噪声取值的概率分布服从高斯分布的信号称为高斯白噪声。
无线电通信中,需要发射的信号首先要调制到大载波信号上再发射出去,发射信号通过信道传输[6]。传输过程中,已调波信号会受到各种干扰,图1中加入的是比较常见的加性噪声——高斯白噪声N(t)。最后对接收到的信号进行分析,估计信号的功率谱。图1中接收到的信号


图1 信号传输模型
2 高阶谱估计
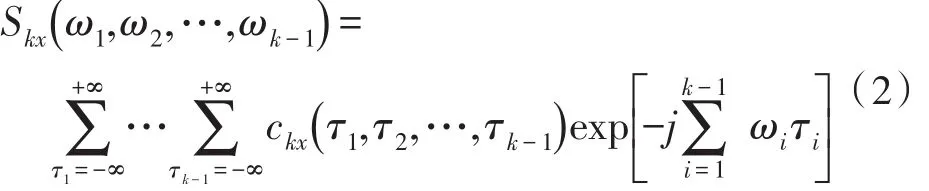
通常Skx(ω1,ω2,…,ωk-1) 是复数,上式存在的充分必要条件为
高阶谱估计的方法可分为参数法和非参数法。参数法是利用观测到的数据来建立所分析过程的参数模型,理论上的频率分辨率是不受限与观测数据的长度,可得到分辨率较高的谱估计。非参数法则是在傅里叶变换的基础上,借助于FFT算法,易于得到物理意义明确的谱估计。但频率分辨率受限于观测数据的长度。无论是参数法还是非参数法,选择合理地参数模型和模型阶数是极为重要的。
2.1 非参数法谱估计
2.1.1 直接法
把随机序列x(n)分为K段,每段含偶数M个样本,并减掉各自的平均值。(也可对信号加窗处理来减小方差。)为满足FFT算法,每个数据可补零。第i段数据的DFT(离散傅里叶变换)系数为
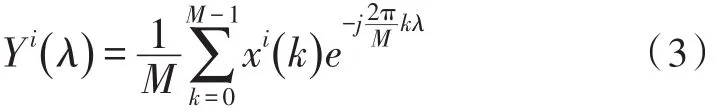
令M=M1N1(M1为奇正整数),M1=2Jn+1,进行频域平均估计n阶矩谱为
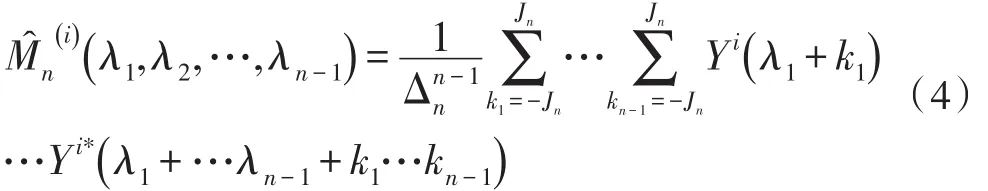
式中,i=1,2…,K,Δnn-1是频率样本间需要的间隔,
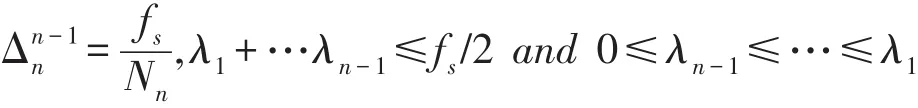
最后对K段数据求平均值的序列的n阶谱估计,为

其中
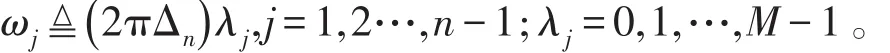
以上叙述的直接法对序列进行双谱估计,可由MATLAB中高阶功率谱工具箱中的bispecd.m和bispecdx.m实现。
2.1.2 间接法
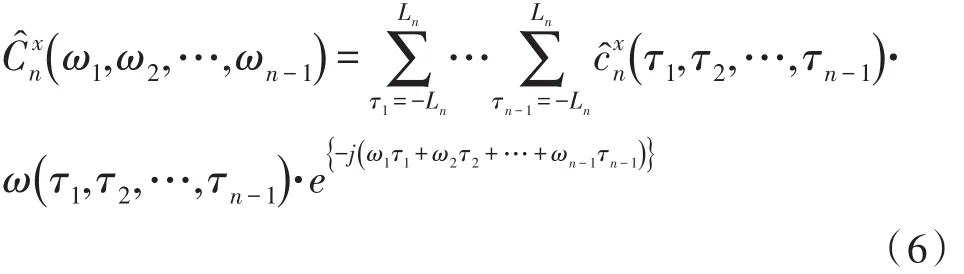
以上叙述的间接法对序列进行双谱估计,可由MATLAB中高阶功率谱工具箱中的bispeci.m实现。
2.2 参数法谱估计
参数法谱估计的对象只能是线性过程。
设为非高斯独立同分布信号,通过单位脉冲函数响应为的时不变系统,加上加性噪声为高斯(白)噪声,得到输出的k阶累积量为

输出y(n)的k阶统计量为
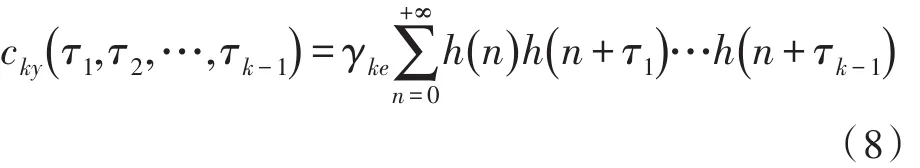
则y(n)的k阶谱为
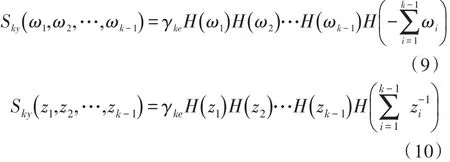
对于比较常用的双谱有
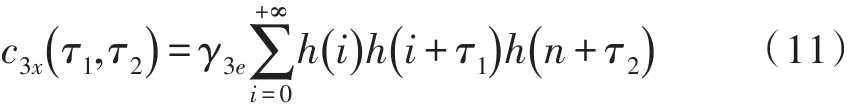
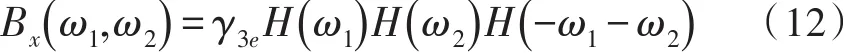
3 功率谱的仿真
双谱估计可由MATLAB中高阶功率谱工具箱中的bispect.m实现[13]。其双谱图如图2、3、4所示。
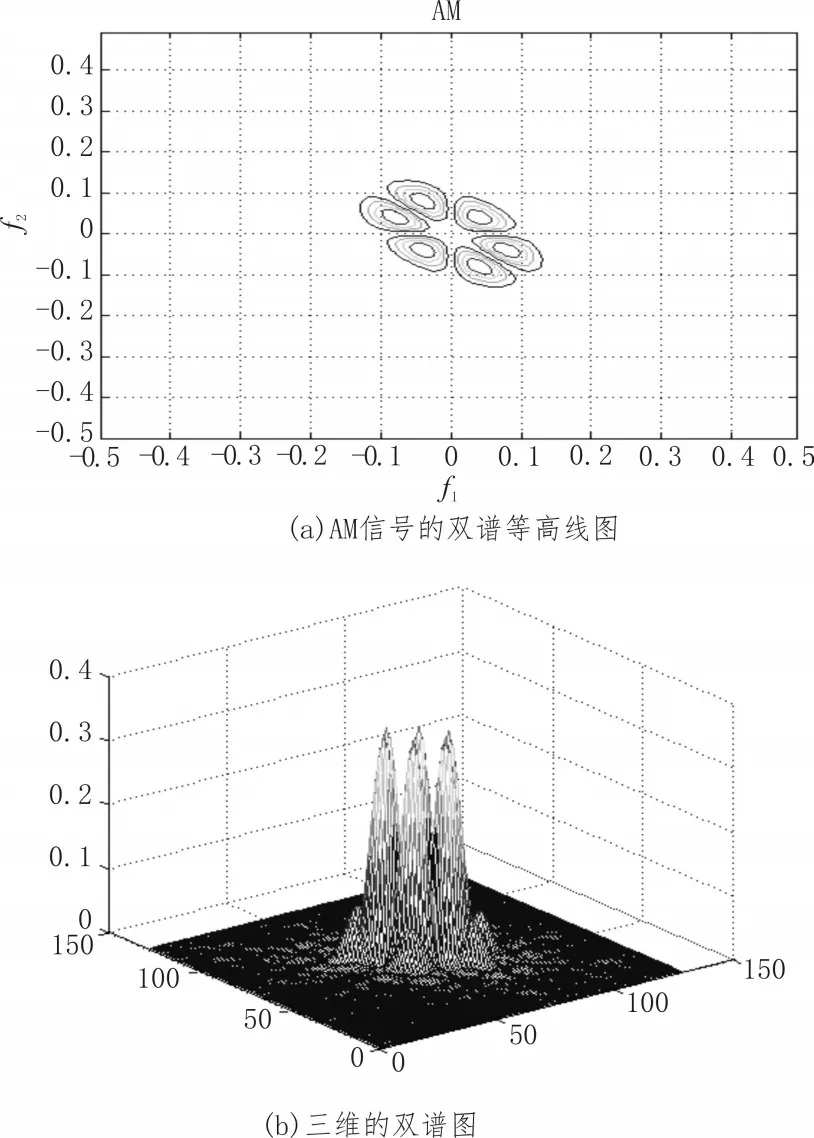
图2 AM信号的双谱图
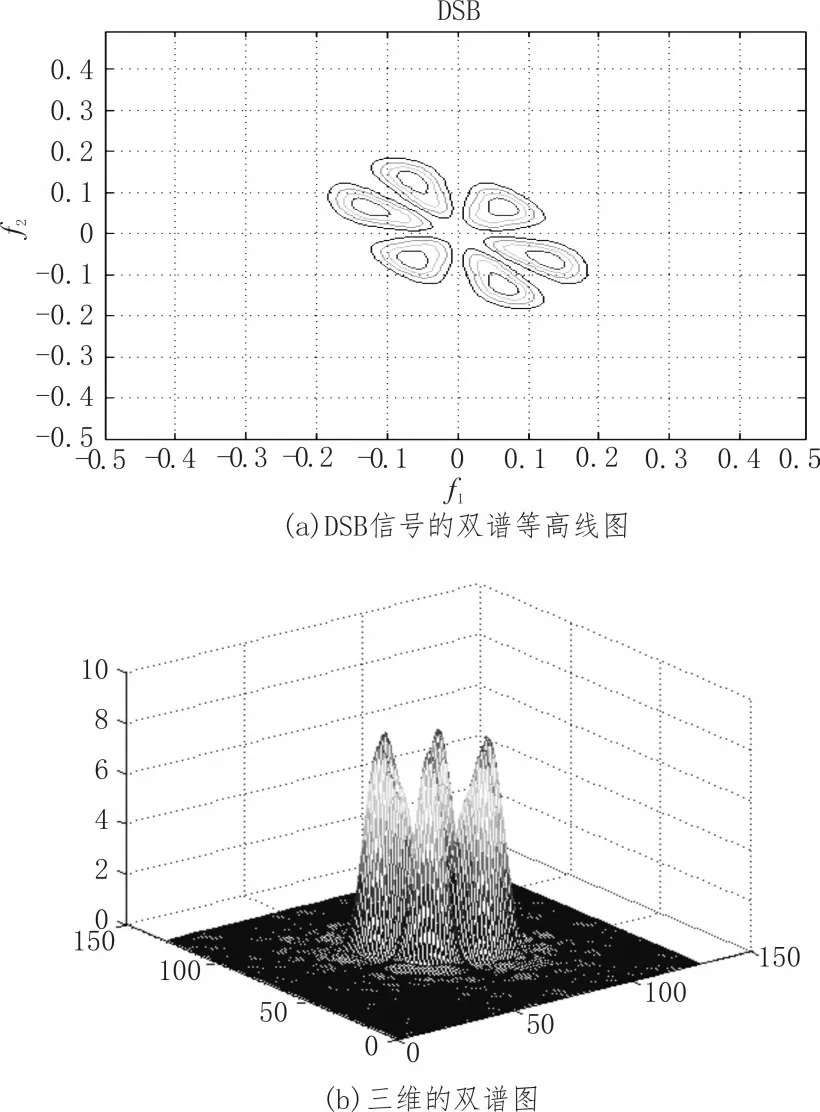
图3 DSB信号的双谱图
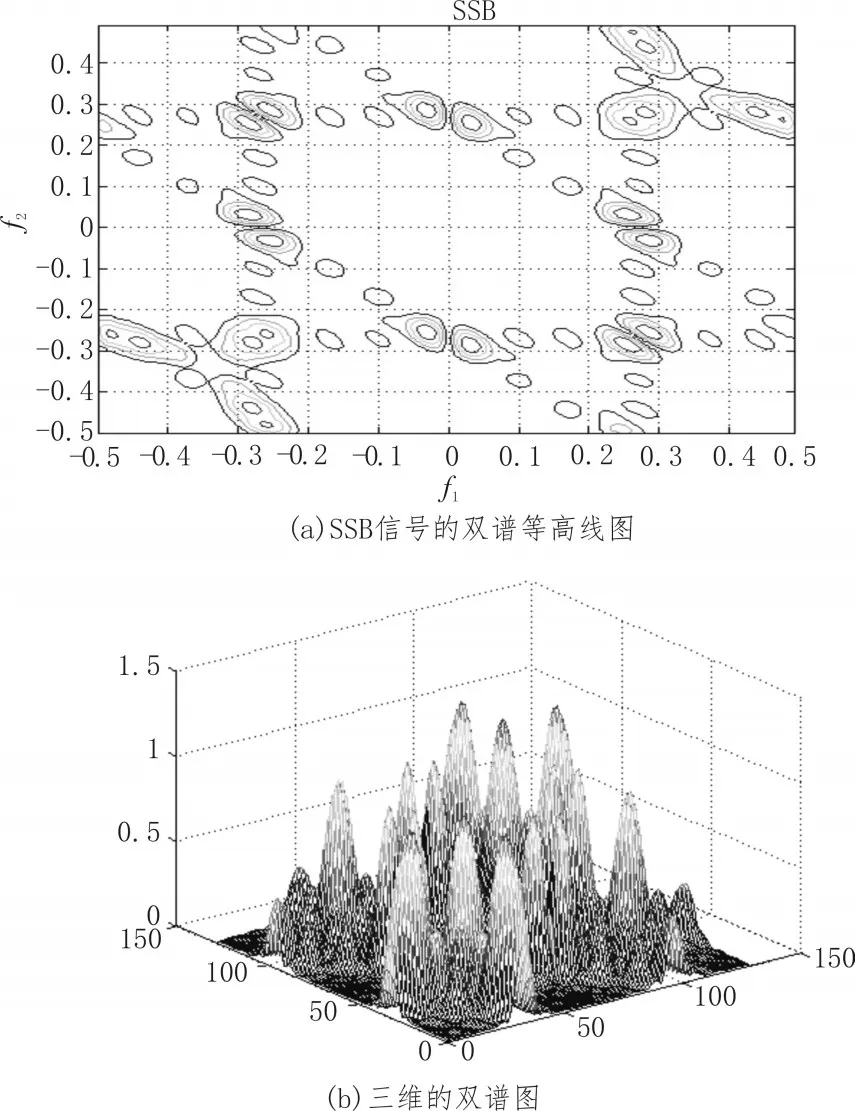
图4 SSB信号的双谱图
从图3、图4的双谱分析图中可以看出来DSB的信号抗噪声能力要强于SSB的信号抗噪声能力。
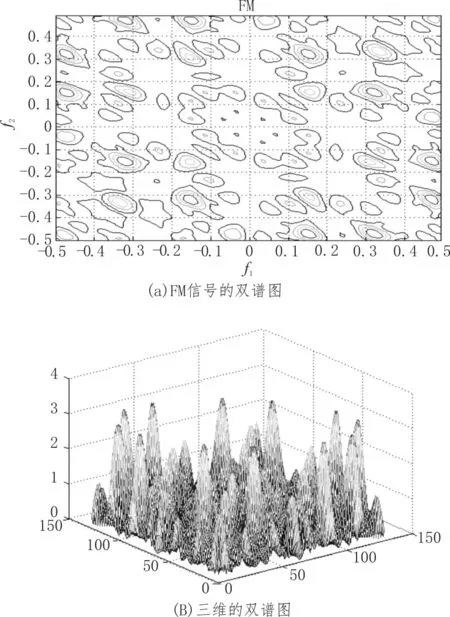
图5 FM信号的双谱图
以上是各种已调信号的双谱的等高线图和三维双谱图。双谱中有6个对称区域,不含丢失的相位信息。信号抗噪声能力越强(WBFM>DSB>SSB>AM or NBFM),双谱图中等高线分布越集中。此方法常用于测试机器是否有故障[15]。
4 结论
高阶谱估计提高了谱估计的分辨率。并通过双谱和三维双谱分析可以清晰的看出:双谱中有6个对称区域,不含丢失的相位信息。红色等高线是主要的频率分布区域。信号抗噪声能力强弱——信号抗噪声能力越强(WBFM>DSB>SSB>AM or NBFM),双谱图中等高线分布越集中。
[1]沈再阳.精通MATLAB信号处理[M].北京:清华大学出版社,2015.
[2]李庆岩.无线信号调制模式识别技术的研究[D].北京:北京交通大学,2014.
[3]谢鑫,李国林,姚江涛.近程无线电信号的自动识别[J].通信学报:2005,28(2):29-31.
[4]宫雅利.浅谈无线电通信技术的发展现状[J].信息与电脑(理论版):2011,11(2):77-89.
[5]牟泽慧.无线电信号辨别[J].品牌:2014(11):155-156.
[6]郑薇,赵淑清,李卓明.随机信号分析(第三版)[M].北京:电子工业出版社,2015.
[7]邱天爽,郭莹.信号处理与数据分析[M].北京:清华大学出版社,2015.
[8]李永新,吴健.信号与动态测量系统[M].北京:人民邮电大学出版社,2014.
[9]孙君.无线电通信发展与创新分析[J].通讯世界,2016(3):11-13.
[10]唐智灵,杨小牛,李建东.调制无线电信号的分形特征研究[J].物理学报,2011,60(5):1-7.
[11]赵晓晖.谱估计与自适应信号处理教程[M].北京:电子工业出版社,2013.
[12](美)Petre Stoica和Randolph L.Moses著.现代信号谱分析[M].吴任彪,韩萍,冯青等译.北京:电子工业出版社,2012.
[13]赵红怡,张常年.数字信号处理及其MATLAB实现[M].北京:化学工业出版社,2002.
[14]苟飞.随机信号处理的新方法——神经网络及高阶谱[D].广州:华南理工大学,1995.
[15]轴承数据的MATLAB分析.[EB/OL].http://www.kongzhi.net/cases/caseview.php?id=8979.2011.
[16]张小慧.信号高阶谱分析及在地震勘探中的应用[D].四川:成都理工大学,2012.
