等离子体光栅靶的表面粗糙度对高次谐波产生的影响∗
2018-01-18李夏至邹德滨周泓宇张世杰赵娜余德尧卓红斌2
李夏至 邹德滨 周泓宇 张世杰 赵娜 余德尧 卓红斌2)
1)(国防科学技术大学理学院,长沙 410073)2)(上海交通大学IFSA协同创新中心,上海 200240)(2017年6月11日收到;2017年7月13日收到修改稿)
1)(College of Science,National University of Defence Technology,Changsha 410073,China)2)(IFSA Collaborative Innovation Center,Shanghai Jiao Tong University,Shanghai 200240,China)
1 引 言
极紫外到软X射线频段的辐射光源在诸多研究领域有着广泛应用.在物质科学领域,极紫外光可用于原子光谱和固体光谱的测量以及金属磁化动力学特性的探测[1−3].此外,由于极紫外光的波长远小于红外光,将极紫外光脉冲用作瞬态表面声波研究中的探针,可极大地提高系统的分辨率[4].以往人们基于传统加速器利用同步辐射和自由电子激光来产生该频段的辐射[5,6].然而,巨大的体积和高昂的成本严重限制了其实际应用.
随着超短超强激光脉冲技术的发展,研究人员发现超强激光与固体密度的等离子体靶相互作用可有效激发高次谐波,这推动了紧凑型X光源研究的不断发展.基于超强激光驱动等离子体固体靶产生高次谐波这一物理机制,国内外研究人员开展了大量的理论分析、数值模拟和实验研究,相继提出了多种高次谐波的产生机制和理论模型[7−12].其中,针对相对论激光与普通平面靶相互作用,研究人员提出了相对论振荡镜模型[13−15]和相干尾波发射模型[16]两种高次谐波激励机制.最新的研究发现,采用具有周期性表面结构的光栅靶取代平面靶,可以对高次谐波进行频域和空间分布上的调制.基于表面电流模型[17],我们分析并研究了线(P)极化[18]和圆极化[19]两种极化模式的超短超强激光脉冲垂直照射光栅靶激发高次谐波的物理机理及其辐射特性.研究结果表明,由激光场作用下的相对论电子振荡所产生的沿靶表面定向发射的高次谐波,在光栅的干涉作用下,特定阶数的谐波被明显增强.Lavocat-Dubuis和Matte[20]利用粒子模拟方法验证了在相对论强度(I0≥1.37×1018W/cm2)的激光作用下固体密度的等离子体光栅靶对高次谐波具有明显的调制效果,模拟结果表明强激光激发出的谐波其强度在空间上的分布并不均匀,仅在特定方向存在特定阶数的谐波.2013年,Cerchez等[21]在实验上进一步验证了上述设想,在实验中成功观测到具有一定发射特性的高次谐波以及光栅对特定阶数谐波的增强效果,其后续的数据分析表明,实验在平行于光栅表面方向上获得了高达45阶的高次谐波.不过,实验结果同时显示[21],高次谐波的频谱成分与理论预期结果存在一定差异.其中,制靶工艺精度、靶在光压下解体和激光的波前弯曲均可能影响理想光栅结构,改变光栅的调制效果,并最终导致理论和实验存在差异.
本文引入表面粗糙度这一概念来表征光栅靶结构固有的缺陷,在此基础上对高次谐波的产生机理以及辐射特性进行了细致的分析和研究.这里需要指出的是,本文所研究之表面粗糙度是靶的固有属性,和外加激光场无关,这点和由激光脉冲波前弯曲以及光压导致的靶的解体有着本质区别.研究结果表明,光栅靶表面粗糙度明显改变光栅的光学调制效果,直接影响高次谐波的频谱分布和辐射角分布.随着靶表面粗糙程度的增大,光栅匹配条件逐渐失效,高次谐波能量向各阶分散,且辐射张角逐渐偏离平行于靶表面的方向.
2 物理模型
等离子体光栅结构如图1(a)所示,实线表示理想光栅,虚线表示考虑表面粗糙度的光栅外包络.理想光栅的周期为l,齿宽为w,齿高为h,总长度为L.为简化分析,光栅靶的表面粗糙度采用高次正弦函数的表示形式,即f=A{[1+sin(y/lb)/2]}a,其中lb为包络周期,A是衡量粗糙程度的振幅,a是函数阶数,简单起见其值在本文中恒取2.
考虑一束P极化超短超强激光脉冲沿y方向垂直入射到固体密度的等离子体光栅靶表面,激光的波长λ=1µm.利用表面电流模型[17],由超强激光驱动的等离子体表面电流所激发的n阶谐波的单位固体角辐射功率可以表示为[18]
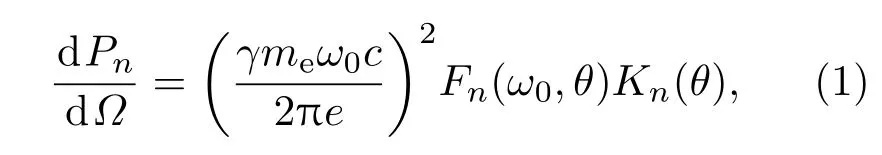
式中,γ是相对论因子,me是电子静止质量,ω0是入射激光频率,c是真空中的光速,e是电子的带电量,θ是出射方向和等离子体边界的夹角,Fn(ω0,θ)是干涉系数,Kn(θ)是单电子辐射角分布且满足[18]

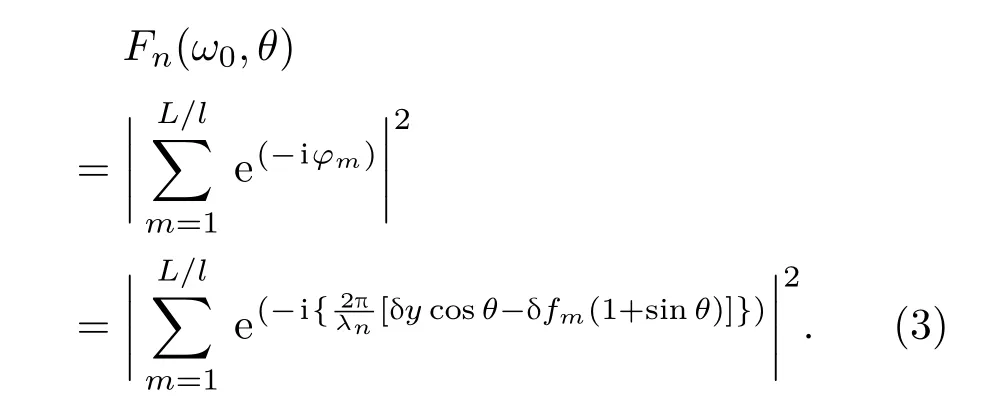
对于光滑的光栅结构,表面粗糙度的振幅A取0,(3)式退化为理想状态下光栅的干涉系数若总长度L远远大于周期l,(4)式进一步退化为
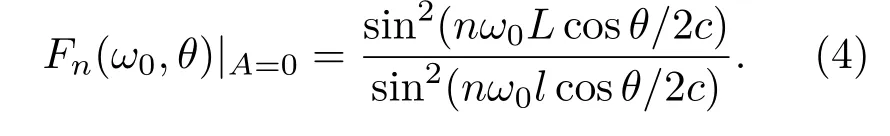
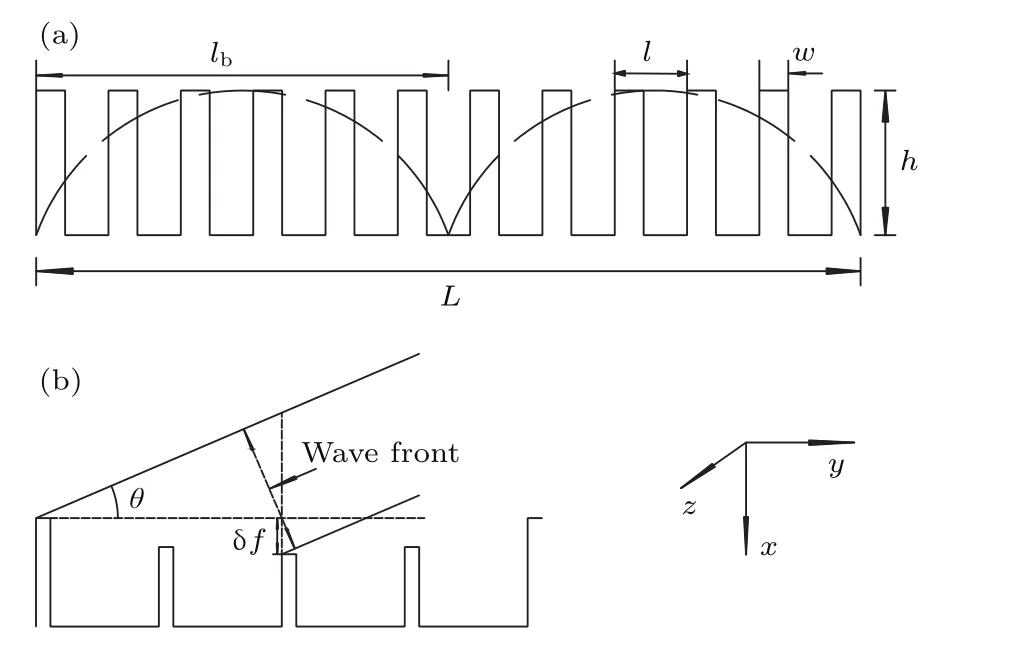
图1 (a)光栅结构示意图;(b)光路示意图Fig.1.(a)System schematic of grating;(b)schematic of the light path.
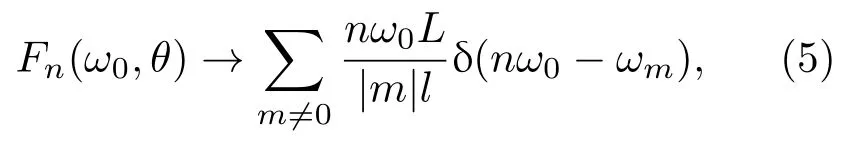
其中ωm=2π|m|c/lcosθ,m取整数.可见,若令θ=0,则仅在nω0=ωm时,干涉系数的值不为零且取极大值,谐波阶数为m=nλ/l.这样,可以推测,对于周期为λ/4的等离子体光栅,仅谐波阶数为4n的谐波才会在平行于靶表面的方向得到增强.

图2 不同阶数谐波干涉系数的角分布 (a)4阶谐波的干涉系数;(b)5阶谐波的干涉系数;黑色曲线为理想光栅,红色曲线为表面振幅取λ/16Fig.2.Angle distribution of different orders harmonics interference factors:(a)and(b)stand for the 4th and 5th order harmonics,respectively.Black lines represent ideal grating while red lines stand for A=λ/16.
图2给出了4阶谐波和5阶谐波干涉系数的角分布,光栅的周期取λ/4,其中黑色实线代表理想光栅,红色实线代表表面粗糙度的振幅取λ/16时的粗糙光栅.从图2(a)可以看出,对于4阶谐波,两种光栅的干涉系数在平行于和垂直于靶表面方向均存在张角(半高全宽)分别为11°和1°的两个峰,表面粗糙度的引入使得干涉系数的峰值降低30%.对于理想光栅,随着角度的增大,干涉系数呈现先降低再升高的趋势.而对于粗糙光栅,干涉系数的角分布中几乎各个角度上都出现了若干个半高全宽均不等的峰.与图2(b)比较发现,对于满足光栅匹配条件的4阶谐波,两种光栅靶干涉系数的峰主要集中在贴近于靶表面方向.对于5阶谐波,在37°方向满足理想光栅的匹配条件,故在这个角度出现了一个较强(约80)且半高全宽较窄(约5°)的峰值.然而,引入表面粗糙度之后,原本集中在37°处的干涉系数峰被分散到了许多不同的角度,同时这些分散的峰强度明显降低,相较理想光栅在37°处的峰值,粗糙光栅的峰值大幅降低约90%.
根据表面电流模型[17],谐波可被近似描述为由存在于等离子体表面的电子在入射激光的作用下做简谐振荡而产生的辐射.光栅齿顶的电子在激光场的作用下振荡,进而激发次级辐射,这一辐射特性由(2)式表征.产生的辐射场在光栅的作用下被调制整形,这一效应则由(3)式表征.联立(1),(2)和(3)式,可以获得受光栅调制形成的辐射远场空间分布Pn.
图3给出了不同表面粗糙度情况下4阶谐波和5阶谐波的远场辐射分布Pn,其中图3(a)—(c)和图3(d)—(f)分别表示4阶谐波和5阶谐波,图3(a)和图3(d)表示不考虑表面粗糙度也即A=0的情况,图3(b)和图3(e)表示表面粗糙度振幅A=λ/16的情况,图3(c)和图3(f)则表示表面粗糙度振幅A=λ/8的情况.对于经理想光栅调制后的4阶谐波,其远场辐射分布具有明显的空间选择性,辐射能量主要沿着靶表面的方向传播,辐射张角约为15°;而对于5阶谐波,与图2(b)保持一致,辐射方向偏离了靶的表面,主要集中在37°的方向,辐射张角约为5°,峰值强度提高了一个数量级.随着光栅靶表面粗糙度的增加,发现4阶谐波和5阶谐波在空间分布上均发生了较大的畸变.此外,辐射远场分布中均出现若干个相对独立的辐射功率峰,沿表面发射的高次谐波逐渐偏离靶表面的方向而向激光反射方向靠拢,且峰值远低于满足光栅匹配条件的情况.这样,理想光栅的辐射频谱中集中在靶表面和特定频段的能量在考虑表面粗糙度后被分散到各个频段以及远离靶表面的各个方向.
在以上的讨论中,分析了4阶和5阶这两阶较低次的谐波,而不是高次谐波.这样做的原因主要有两点:其一,不管是高次谐波还是较低阶的谐波,它们均来自由激光驱动的表面电流所产生的次级辐射,而且在频谱中各阶谐波的增强效果均取决于由光栅结构所决定的匹配条件;其二,高阶谐波的强度远低于低阶谐波的强度,选取低阶谐波进行分析可以在揭示物理原理的基础上较好地避免谱强度过低带来的不便.
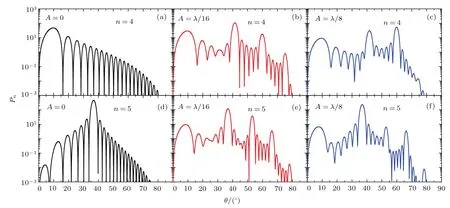
图3 不同靶型和谐波阶数下的辐射远场分布 (a)–(c)代表4阶谐波;(d)–(f)代表5阶谐波;黑色曲线为理想光栅;红色曲线为A=λ/16;蓝色线条为A=λ/8Fig.3.Radiation distribution of different harmonic orders for the ideal and rough grating targets:(a)–(c)stand for the 4th order harmonic;(d)–(f)stand for the 5th harmonic.Black,red and blue curve lines represent ideal grating,A= λ/16 and A= λ/8,respectively.
3 粒子模拟结果与讨论
为验证以上理论结果,利用二维粒子模拟程序EPOCH对激光与光栅靶相互作用激发高次谐波的过程进行了数值模拟.模拟中,一束波长λ=1µm的P极化激光垂直入射于具有不同表面粗糙度的等离子体光栅靶.激光脉冲的时空分布为q(r,t)=q0sin(2πt/t0)exp(−r2/r20),其中q0=3为激光的归一化振幅,所对应的强度为I0=1.233×1019W/cm2,束腰半径r0=3λ,脉冲持续时间为五倍激光周期即5T0,同时t0=10T0.等离子体光栅靶的密度为600nc,其中nc=meω20/4πe2是等离子体临界密度,e和me分别为电子的电荷和静止质量,ω0为激光的中心频率.对于A=0的理想光栅,选取周期l=λ/4,齿宽w=λ/16,齿顶高h=λ/8,长度L=6λ;对于粗糙度光栅靶情况,表面粗糙度的振幅分别取A=λ/16和A=λ/8,外包络的周期为λ,其他参数和理想光栅一致.模拟盒子的尺寸为x×y=5λ×20λ,网格精度为400/λ×1000/λ,每个网格放置36个宏粒子,初始设置为冷等离子体.
图4给出t0=12.5T0时刻不同表面粗糙度情况下电场的kx×ky空间分布,其中图4(a)中的靶不考虑表面粗糙度的理想光栅,图4(b)中的靶为表面粗糙度振幅取λ/16的光栅,图4(c)中的靶为表面粗糙度振幅取λ/8的光栅,图中的黑色曲线为kx=0方向的一维谐波频谱分布.从图4(a)可以看到,对于理想光栅,在平行于靶表面的方向上出现了较为明显的4n阶谐波,辐射强度在高次频段仍保持较高的水平,辐射张角随着谐波阶数的上升变小;对于特定阶数的谐波在远离靶表面的区域,其强度变弱,辐射张角变窄.同时,由于m/=4n阶谐波在平行于靶表面的方向并不满足光栅的匹配条件,所以在沿着靶表面的方向,这些阶数的谐波强度相对于4n阶谐波非常低,因此在图4(a)中并未观察到明显的m阶谐波.对于表面粗糙度分别为A=λ/16和A=λ/8的光栅,比较图4(b)和图4(c),发现在电场的二维傅里叶频谱中出现了几乎各个整数阶的谐波,仅个别阶数的谐波从频谱中缺失.如图4(c)中kx=0方向,在靶表面的区域内,谐波的能量主要集中在较低的频段,高次谐波的强度下降很快;在远离靶表面的方向,可以观察到明显偏离靶表面方向的辐射,在0°—90°的空间范围内出现了许多辐射张角很小的谐波峰值点,谐波被散射到整个空间.以上模拟结果与表面电流模型所预测的结果符合较好,且与Crèches等[21]的实验结果基本一致.
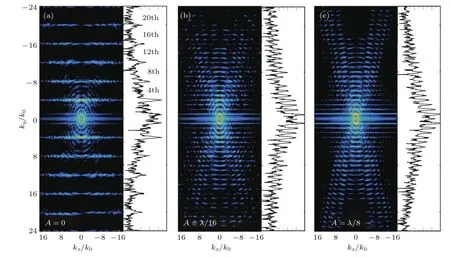
图4 不同表面粗糙度条件下谐波辐射场分量的二维傅里叶频谱 (a)A=0;(b)A=λ/16;(c)A=λ/8;图中一维黑色曲线为kx=0方向的截线图Fig.4.Two-dimensional Fourier transformation to the radiation component of different target surface roughness:(a)A=0;(b)A= λ/16;(c)A= λ/8.Curve line is the one-dimensional spectrum in the direction kx=0.
4 结 论
通过理论和数值模拟方法研究了超短超强激光与光栅靶相互作用过程中光栅靶的表面粗糙度对高次谐波发射特性的影响.研究发现,表面粗糙度对光栅靶的光学特性影响很大,改变了光栅的干涉系数,导致高次谐波辐射远场分布畸变.原本集中在靶表面传播的特定阶数的谐波逐渐分散到远离靶表面的各个方向以及各阶谐波,且高次谐波的频谱成分并不完整.上述结果与文献[21]中实验观察到的结果基本符合.
[1]Haight R,Seidler P F 1994Appl.Phys.Lett.65 517
[2]Cavalieri A L,Müller N,Uphues T,Yakovlev V S,Baltuska A,Horvath B,Schmidt B,Blümel L,Holzwarth R,Hendel S,Drescher M,Kleineberg U,Echenique P M,Kienberger R,Krausz F,Heinzmann U 2007Nature449 1029
[3]La-O-Vorakiat C,Siemens M,Murnane M M,Kapteyn H C,Mathias S,Aeschlimann M,Grychtol P,Adam R,Schneider C M,Shaw J M,Nembach H,Silva T J 2009Phys.Rev.Lett.103 257402
[4]Tobey R I,Siemens M E,Murnane M M,Kapteyn H C,Torchinsky D H,Nelson K A 2006Appl.Phys.Lett.89 091108
[5]Abo-Bakr M,Feikes J,Holldack K,Kuske P,Peatman W,Schade U,Wüstefeld G,Hübers H W 2005Phys.Rev.Lett.90 094801
[6]Jeong Y U,Kazakevitch G M,Cha H J,Park S H,Lee B C 2003Nucl.Instrum.Meth.543 90
[7]Li K,Zhang J,Yu W 2003Acta Phys.Sin.52 1412(in Chinese)[李昆,张杰,余玮2003物理学报52 1412]
[8]Li X X,Xu Z Z,Tang Y 1997Acta Phys.Sin.46 267(in Chinese)[李学信,徐至展,汤燕1997物理学报46 267]
[9]Zhang Q J,Sheng Z M,Zhang J 2004Acta Phys.Sin.53 2180(in Chinese)[张秋菊,盛正明,张杰 2004物理学报53 2180]
[10]Ge Y C 2008Acta Phys.Sin.57 4091(in Chinese)[葛愉成2008物理学报57 4091]
[11]Du H,Zhang H D,Zhang J,Liu H F,Pan X F,Guo J,Liu X S 2016Chin.Phys.B25 113201
[12]Luo X Y,Ben S,Ge X L,Wang Q,Guo J,Liu X S 2016Acta Phys.Sin.65 123201(in Chinese)[罗香怡,贲帅,葛鑫磊,王群,郭静,刘学深2016物理学报65 123201]
[13]Grebogi C,Tripathi V K 1983Phys.Fluids26 1904
[14]Bulanov S V,Naumova N M,Pegoraro F 1994Phys.Plasmas1 745
[15]Norreys P A,Zepf M,Moustaizis S,Fews A P,Zhang J,Lee P,Bakarezos M,Danson C N,Dyson A,Gibbon P,Loukakos P,Neely D,Walsh F N,Wark J S,Dangor A E 1996Phys.Rev.Lett.76 1832
[16]Thaury C,Quéré F,Geindre J P,Levy A,Ceccotti T,Monot P,Bougeard M,Réau F,D’Oliveira P,Audebert P 2007Nat.Phys.3 424
[17]Brownell J H,Walsh J 1998Phys.Rev.E57 1075
[18]Zhang S J,Zhuo H B,Zou D B,Gan L F,Zhou H Y,Li X Z,Yu M Y 2016Phys.Rev.E93 053206
[19]Yu W,Yu M Y,Zhang J,Xu Z 1998Phys.Rev.E57 R2531
[20]Lavocat-Dubuis X,Matte J P 2010Phys.Plasmas17 093105
[21]Cerchez M,Giesecke A L,Peth C,Toncian M,Albertazzi B,Fuchs J,Willi O,Toncian T 2013Phys.Rev.Lett.110 065003
