轴表面荧光磁粉检测缺陷图像的快速展开拼接

，， , ,2

(1.南京理工大学 机械工程学院，南京 210094;2.常州信息职业技术学院 电子与电气工程学院， 常州 213164)

磁粉缺陷检测是金属工件表面无损检测的重要手段。由于荧光磁粉法的检测灵敏度高于黑色磁粉法的，且检出率更高，故在工业上被广泛应用。传统的荧光磁粉检测需依靠工人在紫外光环境下手动操作设备，不仅劳动强度大，还会造成错检和漏检，并且对眼睛和皮肤也有一定的伤害。机器视觉检测技术[1]可在多方面改善现有检测方法的不足，一方面，检测硬件上只需要在现有设备基础上增加图像采集装置，对原有设备的改造成本低；另一方面，利用成像处理识别技术可以替代人工辨识，从而排除人为因素的干扰，既减轻了工人的负担，又提高了检测速度以及检测结果的准确性和一致性[2-6]。

从理论上来说，用线阵CCD(电荷耦合元件)相机配合轴自身的旋转可完整地扫描拍摄轴类工件的外表面[7]。但实际上，一方面，工件由通电铜盘夹紧，视觉检测系统只有简易的中心标记，没有对中装置，不能保证工件轴的中心处于设备的旋转中心，一旦没有严格对中，就无法采集完整的侧面图像；另一方面，系统被检对象的外形结构多样(轴类、方件、塔形件等)，无法用同一套机械结构匹配线阵相机的扫描拍摄，所以系统选用了面阵CCD相机。针对轴类工件的检测，面阵相机获取的侧面图像存在几何失真现象，直接对失真图像的缺陷进行测量存在很大的误差。因此，在进行缺陷特征尺寸测量之前，必须对所获取的轴侧面图像进行展开校正处理。由于轴是旋转体，面阵相机无法单次采集到完整的侧表面图像，所以需要将局部图像拼接成完整的侧面展开图，以便进行后续的图像处理，并获得更加准确和全面的检测结果。

目前，侧表面图像展开校正方法通常以原检测图像中某几个特征点为控制点，直接计算图像间透视变换矩阵来实现图像校正，如基于局部透视变换的圆柱体侧表面条码矫正方法[8]适合工件表面纹理确定、控制点易选择的情况，对于纹理稀少，没有明确可用控制点的轴类工件，侧表面图像展开校正方法则无法适用。针对上述问题，笔者提出了一种针对轴侧表面缺陷图像的展开算法，依据推导出的变换公式实现对原工件图的坐标展开，并用双线性法对展开后的图像进行插值[9]，快速地生成了轴侧表面展开图像。对于展开后缺陷图像的拼接，由于磁粉缺陷图像特征点少，笔者结合基于相位相关的柱面图像拼接技术[10]，从相邻图像频域的相位信息获取平移关系，克服了图像光照变化和镜头畸变对拼接的影响，最终实现展开图的拼接。为轴侧表面缺陷几何特征量的测量准确度提供了保障。

1 图像获取及侧面图像失真分析

1.1 图像获取

在视觉检测系统中，由于无法一次性采集到轴类工件侧表面的完整图像，所以图像采集需配合运动机构完成。图像采集系统扫描拍摄原理示意如图1所示，图 1(a)为轴类零件的右视图，采集轴类图像时，相机固定，工件每次旋转60°，即侧面分6个位置依次拍摄;图 1(b)为工件正视图，相机视场覆盖工件200 mm长度，一段工件的侧面拍摄完成后，相机沿水平方向移动150 mm，保证一部分重叠率，再次采集图像，直至将轴类工件侧面的所有图像全部采集完毕为止。

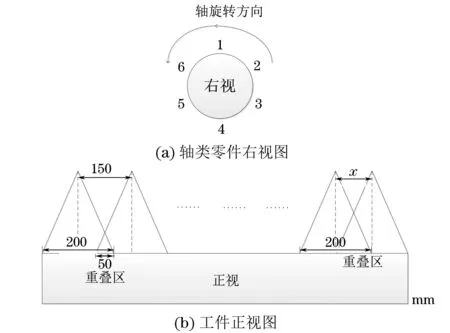
图1 图像采集系统扫描拍摄原理示意

因此，采集的图像不仅包含了轴侧表面的所有缺陷信息，并且满足了一定的重复率。可以将每张图片中包含轴侧面的部分进行展开，对相邻的图片进行拼接，即可获得整个轴类工件的侧面展开图，以便测量分析。

1.2 侧面图像失真分析

图像采集完成后，所获得的轴侧面图像存在两种形式的失真，即径向畸变和透视失真。

径向畸变是由镜头的光学特性产生的，其原因是光线穿过透镜不同位置时的弯曲程度不同，光线离透镜轴线越近，弯曲程度越小，图像畸变越小；光线离透镜越远，弯曲程度越大，图像畸变越大。为了校正径向畸变，采用径向畸变矫正法[11]，这需要获取相应的畸变系数，再做畸变的相反变换，即可消除畸变。文中的图像在展开前，已经用上述方法完成了径向畸变的矫正。

透视失真是由在实际拍摄过程中，镜头光轴与目标平面不垂直产生的。如果被拍摄对象是平面，通过调整相机拍摄角度，使镜头轴线与被拍摄平面的法线平行，则可减少透视误差。由于轴的侧表面是曲面，而面阵相机搭载的CCD传感器接收面为平面，所以拍摄时的透视失真是必然存在的。

2 轴侧表面缺陷图像的展开拼接算法

(1) 建立相机成像模型，获取坐标对应关系。根据成像模型的仿射变换关系，结合插值算法完成像素复制，实现轴侧面检测图像的展开校正。

(2) 轴侧表面展开图像的拼接。利用相位相关原理，从相邻图像展开图的重叠区域获取图像的平移位置信息，最终对图像进行径向和轴向的双向拼接。

2.1 相机成像建模及侧面展开算法

相机成像模型包括线性和非线性模型。对于线性相机成像模型，直接采用透视投影方式获取侧表面空间点或展开平面空间点与图像坐标之间的位置关系；而对于非线性相机成像模型，因其存在不同程度的畸变，所以使得空间点所成的像并不在线性模型所描述的位置上，可引入非线性畸变值进行修正。特别对于相机视场较小，检测工件尺寸到相机距离也较小的情况，透视投影关系可通过光学成像过程进行几何推导。

相机成像几何模型示意如图2所示，建立的坐标系如下所述。

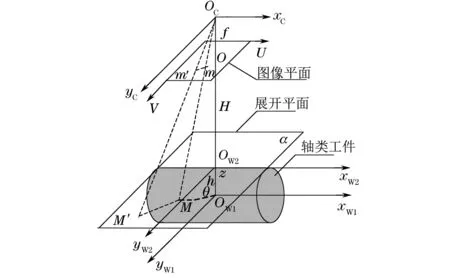
图2 相机成像几何模型示意

(1) 相机坐标系，xCyCz是以OC点为原点的三维坐标系，xC,yC分别与图像的U,V轴平行，z轴为相机光轴，其与图像平面垂直，垂直交点O为图像坐标系原点。

(2) 图像坐标系，UOV是以垂直交点O为原点建立的二维坐标系。

(3) 对世界坐标系1，xW1yW1z是以相机光轴与轴类工件中心线交点OW1为原点的三维坐标系，xW1,yW1分别与图像的U,V轴平行。

(4) 对世界坐标系2，xW2yW2z是以相机光轴与距相机最近轴母线为基准的三维坐标系，以平面交点OW2为原点，xW2,yW2也分别与图像的U,V轴平行，图像平面距展开平面距离为H。

为了获取轴类工件侧表面空间点与图像坐标位置之间的透视投影关系，首先设轴侧面上任一点M在世界坐标系xW1yW1z中的坐标为(x,y,z)，轴半径为R，点M在yW1Oz平面内的投影点与OW1的连线和z轴的夹角为θ。平面α为轴侧面展开平面，M′为M在展开平面上的对应点，其所在平面为xW2yW2O，M′在该坐标系下坐标为(x1,y1)。UV平面为成像平面，m与m′分别为M与M′在该平面的成像点，坐标为(i,j)和(i1,j1)。轴类工件侧表面在成像平面中所形成的图像中心为(i0,j0)，轴侧表面展开平面形成的图像中心为(i10,j10)，由比例关系可得到

(1)

式中：dx和dy分别为相机的像元尺寸；f为相机焦距；h为点M与圆轴最高点间的垂直距离，满足h=R-z=R(1-cosθ)。

则轴类工件侧表面空间点与图像坐标位置之间的透视投影关系可表示为

同理，以距相机最近轴母线为基准展开的平面空间点与图像坐标位置之间的透视投影关系为

轴侧表面空间点与距相机最近轴母线为基准展开的平面空间点之间的坐标位置关系由几何坐标转换得到，如式(4)所示。

(4)

轴侧表面点与展开平面点在图像坐标系中的映射点之间的仿射变换关系由式(2)，(3)，(4)推导建立。

侧表面图像展开时，根据轴侧表面点与展开平面点在图像坐标系中的映射点之间的仿射变换关系，采用双线性插值法对展开后图像进行插值。

2.2 图像的展开拼接算法

检测系统对整个轴侧面采用单次间隔60°，共分6次拍摄完成，每次将拍摄的侧面按照上一节中的算法展开得到6幅展开图。此外，由于单次拍摄的轴长度为200 mm，所以对于长度较长的工件，在长度方向上也需要进行拼接。两次拼接的顺序是先进行周向拼接，然后进行轴向拼接。

图像拼接的关键在于找到两幅图像中重叠部分的平面位移关系。相位相关位移法原理示意如图3所示，两幅存在转动关系的f1(x,y)与f2(x,y)在空域中的关系如式(6)所示。

f1(x,y)=

f2(xcosθ0+ysinθ0-x0,-xsinθ0+ycosθ0-y0)(6)

式中：θ0为转动角度；(x0,y0)为平移距离。

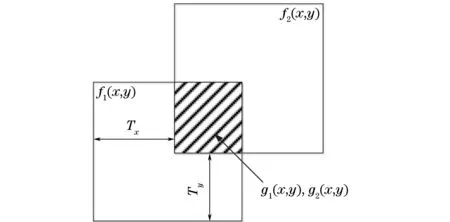
图3 相位相关位移法原理示意

对式(6)进行傅里叶变换得

mod1和mod2分别为F1和F2的模值，对式(7)两边取模，并采用极坐标形式可得

mod1(ρ,θ)=mod2(ρ,θ-θ0)(8)

从式(8)可以看出，两幅图像之间只存在平移关系。因此可以通过相位相关求出初始定位参数θ0和(x0,y0)，算法的实现步骤如下所述。

(1) 对原始图像进行相位相关计算，在得到的δ函数整列中寻找最大峰值及其周围的峰值，将其对应的平移量定义为平移量区间。

(2) 对区间内的某个平移量Tx，Ty，将其重叠部分记为g1(x,y)与g2(x,y)，对g1(x,y)与g2(x,y)再进行相位相关计算，得到其间的平移量，记为x，y。对于区间内所有的平移量，都可以得到与之对应的x,y。

对于存在旋转关系的两幅图，首先采用上述方法得到旋转角度θ0=arctan(x0/y0)，然后将第二幅图旋转θ0，旋转后得到的图像与第一幅图只剩下平移关系，所以再次采用上述算法得到x0，y0。

3 侧表面展开拼接结果

采用美国NI公司的LabVIEW软件实现了对相关图像处理算法的软件编程，并计算展开拼接的时间。为了验证算法的准确性和可行性，使用大恒水星MER-200-20GM型工业数字摄像机，拍摄距离200 mm，视场大小为200 mm×200 mm，相机分辨率为1 628 像素×1 236 像素。相机像元尺寸dx和dy均为0.005 1。被测件是人为设计加工的轴类缺陷试样，样品直径30 mm，长度400 mm，表面分布3组，共计54个微小缺陷，最小缺陷为设计直径为0.5 mm的圆形缺陷，最大缺陷为设计长度为4 mm的线性缺陷。原图像中心(i0,j0)为(812,116)，通过圆柱侧面几何展开前后关系与原始图像信息进行计算，得到(i10,j10)为(812,150)，根据上述参数和成像模型，求得轴侧表面与展开平面图像间的仿射变换关系如式(9)所示。

图4 轴类工件侧表面的原始图和展开图

轴类工件侧表面的原始图和展开图如图4所示，采用双线性插值方法对轴侧表面原始图像图 4(a)进行校正展开，展开效果图像如图4(b)所示。原始图中的曲面失真情况得以解决，如图 4(a)中左起第二个缺陷，该缺陷为设计直径为φ2.5 mm的圆形，在图 4(a)中显示为椭圆，并测出缺陷长2.66 mm，宽2.10 mm，长宽比为1.26；而通过展开矫正后的图4(b)测出缺陷长2.69 mm，宽2.48 mm，长宽比为1.08，更加接近于圆形的长宽比1。

结合相位相关的拼接算法完成了对轴周向及长度方向的拼接，对于拼接后图像重叠部分的灰度，采用权重值为1/2的加权平均实现。利用该程序对3段，每段6张，共18张轴类工件侧面展开图进行了拼接试验，图5为拼接后的结果。从图 5可以看出，由于灰度上的差异，两幅图像间存在拼接痕迹，但是从坐标关系上达到了将整个圆周侧面及长度方向拼接的目的，拼接痕迹对后续检测的影响可以忽略。

图5 轴类工件的侧面展开拼接图

表1为实际尺寸与检测尺寸的结果对比，由于展开算法只对图像坐标y方向有影响，所以对比结果中的数据均由y方向参数测得，测量圆形缺陷y方向的直径以及方向角为0°的条形缺陷的宽度。最终得到圆形直径的最大相对误差为3.9%，条形缺陷的最大相对误差为3.3%。

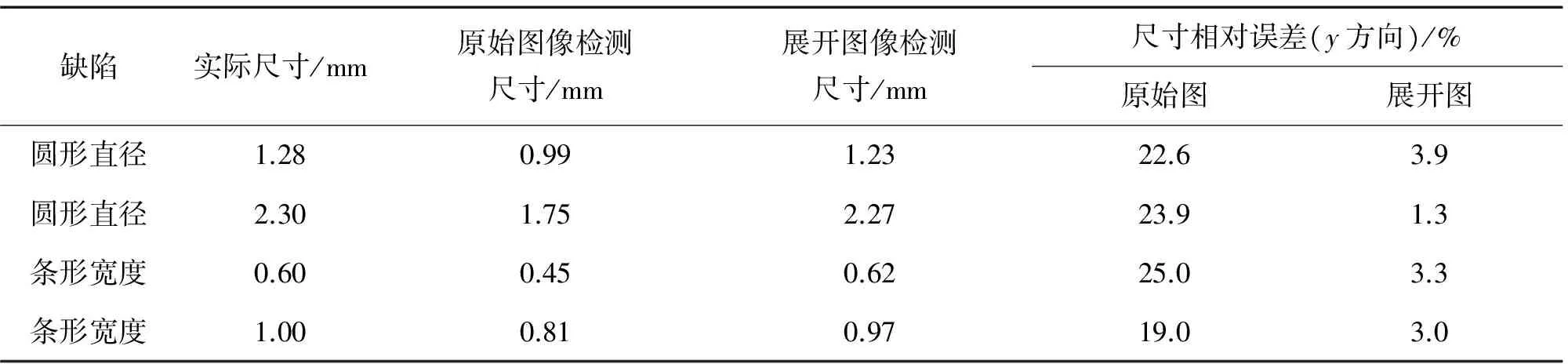
表1 实际尺寸与检测尺寸结果对比

4 结论

针对轴类工件侧表面缺陷检测的成像模型，提供了一种图像的展开拼接算法。算法利用轴类工件成像模型获取检测图和复原图的坐标投影关系，结合双线性插值法，对工件侧表面图像进行快速展开，可解决直接测量外表面缺陷时由于几何失真造成缺陷特征值的测量误差大的问题。利用相位相关法获得相邻图像的平移位置关系，将多张展开图像拼接，生成完整的轴类工件侧面展开图，解决了单一图像无法完整展现全部缺陷的问题，是一种高效实用的方法。从试验结果看，将每张图像的检测区域展开成分辨率为 1 624 像素×250 像素的矩形图像所需的平均时间为0.090 s，展开图像中，圆形缺陷外形尺寸相对误差在3.9%以内，条形缺陷外形尺寸相对误差在3.3%以内。将6幅轴侧面缺陷图像的检测区域展开拼接成分辨率为1 624 像素750 像素的图像所需时间为1.793 s。满足了轴类工件在荧光磁粉无损检测中的对实时性和准确性的要求。在实际检测过程中，待检工件除圆轴类以外，也存在其他形式的曲面，例如圆台工件侧面和塔形工件侧面。因此，笔者提出的展开拼接算法依然有研究、改进和推广的空间。

[1] MARR D. Vision: A computational investigation into the human representation and processing of visual information[M]. Berkeley: University of California Press, 1994:107-111.

[2] 吴平川,路同浚,王炎.机器视觉与钢板表面缺陷的无损检测[J].无损检测,2000,22(1):13-16.

[3] 李桂娟,卜雄洙,杨波,等.中心偏移的全景环形图像快速展开[J]. 光学精密工程, 2012, 34(9): 3-9.

[4] 程文博. 基于机器视觉的注塑制品尺寸检测及表面缺陷识别[D]. 武汉：华中科技大学, 2015.

[5] 李武斌,路长厚,李君,等.圆钢表面缺陷视觉检测技术研究现状与展望[J].无损检测,2012,34(5):54-58.

[6] WANG F,ZHANG S, TAN Z. Nondestructive crack detection of preserved eggs using a machine vision and multivariate analysis[J]. Wuhan University Journal of Natural Sciences, 2017, 22(3):257-262.

[7] 高义林. 基于线阵CCD的车轮表面荧光磁粉探伤系统的研究[D].合肥：安徽大学, 2010.

[8] 黄书海,殷建平,祝恩,等. 基于局部透视变换的圆柱体侧表面PDF417条码矫正方法[J]. 计算机工程与科学, 2012,34(9):93-97.

[9] 王昊京,王建立,王鸣浩,等.采用双线性插值收缩的图像修复方法[J].光学精密工程,2010,18(5):1234-1241.

[10] 李忠新,张登峰,茅耀斌,等.基于相位相关法的柱面全景图拼接技术[J].南京理工大学学报,2002,26(12):43-46.

[11] ZHANG Z. A flexible new technique for camera calibration[J].IEEE. Transactions on Pattern Analysis & Machine Intelligence,2002, 22(11): 1330-1334.