基于逻辑程序的调机路径规划研究
2018-01-18,,2
,,2
(1.桂林电子科技大学 计算机与信息安全学院,广西 桂林541004;2.广西可信软件重点实验室,广西 桂林 541004)
0 概述
随着信息化建设的发展,铁路技术站作业计划的编制由传统的手工作业进入到计算机辅助作业阶段,并逐渐向智能化调度作业阶段发展。技术站作业计划包括了班计划、阶段计划和调车作业计划3个部分,其中与阶段计划编制相关的信息系统的研制和开发大多还停留在数据处理的层次,缺乏辅助决策功能,不能为阶段计划的编制提供决策支持[1]。因此,目前阶段计划的编制仍以人工为主,作业劳动强度大,容易出现计划编制不及时、计划质量低等问题。
调机运用计划是技术站阶段计划的关键内容之一,主要是确定到达列车的解体次序、出发列车的编组次序、调机的作业时间以及承担该作业的调机移动路线,将直接影响铁路货物运输的周转和整个路网的通过能力。如何实现调机运用计划的自动编制是当前研究的重点,其中要解决的问题之一是如何令单个调机的移动路径最短,即单个调机的运用问题。
目前,国内外处理调机运用计划编制问题的方法主要包括:1)数学优化方法[2-3],如动态规划、整数规划和混合整数规划法、拉格朗日松弛算法等。该类方法的优点是具有严格的数学模型,但在编制调机运用计划时通常要处理一些半结构化和非结构化的信息,这些信息来自编制人员手工作业时累积的丰富经验,而这些经验则难以从数学模型的角度严格描述。2)启发式算法[4],如局部邻域搜索算法、迭代搜索算法等。该类算法往往需要仔细地设计一个合理的启发函数,才能在较快的时间内成功避免局部最优,得到最优解。但目前此类算法的设计缺乏统一、完整的理论体系。3)智能优化类算法[5-6],如遗传算法、模拟退火算法、禁忌搜索算法等。此类算法是从随机的可行初始解出发,采用迭代改进的策略去逼近问题的最优解,从理论上讲是一种全局寻优的计算方法,但通常计算量比较大,所需时间较长[7]。
逻辑程序设计是一种声明式的程序设计方法,与传统程序设计方法有较大差异,目前主流的方法有回答集程序设计(Answer Set Programming,ASP)[8]、有限域的约束逻辑程序设计(Constraint Logic Programming over Finite Domains,CLP(FD))[9]等。由于逻辑程序设计方法的模型表达能力强,人工经验可以有效地转变成规则表示的知识库以及编码紧凑、编码方式容易理解等优点,目前越来越受到重视[10-12]。
为了更好地探讨调机路径规划问题的解决途径,本文将尝试通过基于ASP与CLP(FD)的编码方法来解决调机路径规划问题。使用说明性的描述方法将模型和解决过程完全分开,集中考虑模型的建立而不用考虑如何去获得结果,使得编制作业实现自动化。在已有的规则基础上,通过不断增减系统中的规则模拟现实生活中多变的环境,以降低编制作业的劳动强度。
1 基础知识
1.1 回答集程序
ASP是一种基于约束的非单调逻辑程序技术,它把程序解释成在一个文字集上的约束,结果是0个或者多个模型,每个模型对应问题的一个解。与传统的逻辑程序不同的是利用ASP求解问题时,解决问题的答案不是以替换的形式给出,而是由某些原子的集合,即回答集给出。
若A是一个原子,则A或~A称为文字,其中,A为正文字,~A为负文字,A和~A称为一对互补字。每条规则r满足如下形式:
L1orL2or…orLK:-LK+1,…,Lm,notLm+1,…,notLn
(1)
其中,n≥m≥k≥0,每一个Li是一个文字,not表示失败即否定(negation as failure)。将haed(r)={L1,L2,…,LK}称为规则头部,pos(r)={LK+1,LK+2,…,Lm}称为规则体的正文字,而neg(r)={Lm+1,Lm+2,…,Ln}称为规则体的负文字。一个没有规则头部的规则r,称之为约束。如果pos(r)和neg(r)均为空,则称规则r为事实。
设正规逻辑程序P,P相对于原子集合M的Gelfond-Lifschitz规约PM是确定性逻辑程序,PM由以下方法获得:
1)对于P中的任意规则r,如neg(r)M≠,则删除该规则;
2)将剩余所有规则r中的neg(r)删除。
对于原子集合M以及正规逻辑程序P,如果M是程序PM的回答集,则M是程序P的回答集。
本文采用DLV[13]系统中的相关规定,用:-代替←进行书写,每条规则以英文句号结束。
1.2 约束逻辑程序
约束逻辑程序(Constraint Logic Programming,CLP)设计是基于人工智能(AI)中约束满足问题(Constraint Satisfaction Problem,CSP)模型的一种程序设计框架[14]。它继承了逻辑程序设计简单易懂的说明性描述方法,并结合了CSP在求解问题时的效率,使得它在解决很多AI问题时有较好的表现能力。
一个CLP程序[15]是由子句的序列构成的,子句r的形式为:
H←C1,C2,…,CmB1,B2,…,Bn,m≥0,n≥0
(2)
其中,B1,B2,…,Bn为原子公式,C1,C2,…,Cm为约束。特别地,当m=0时,子句形式:H:-B1,B2,…,Bn,而当n=0时,子句表示一种事实。一个原子公式形如:p(t1,t2,…,tn)的表达式(n个变元谓词),其中ti(i=1,2,…,n)称为项。项定义为一个变量,或者一个常量,或者一个作用于n个项的一个函数f(t1,t2,…,tn)。
约束逻辑程序语言(CLP(FD))的约束关系是基于声明的整数运算,是用来实现纯整数之间的关系表达式的计算。程序设计时加入了库(clpfd),它能够更好地联系枚举谓词和更复杂的约束之间关系。
常用的求解器有SWI Prolog、Sicstus Prolog等,本文采用SWI系统中的相关规定,用:-代替←进行书写,每条规则以英文句号结束。
2 问题描述
编组站是我国铁路网络中的重要节点,在这里到达列车会被分散成零散的车厢,出发列车又会由零散的车厢重新组合到一起,其作业组织会直接影响铁路货物运输的效率。首先,到达列车将安排在到达场的合适轨道上展开到达作业,包括摘除干线机车和检查列车的轮轴状态等;接着,由解体调机将列车推送到一个称为驼峰的人造小山峰执行解体作业,当各个去向的车厢将到达驼峰的顶峰时,摘去其与后续车厢相连接的车钩,使其凭借自身重力溜放到轨道上;然后,车厢在调车场中与之前已停留的和后续到达的同去向车厢共同等待满足出发条件完成集结作业;最后,多节车厢满足出发条件被重新组合在一起完成编组作业成为一列新的出发列车,列车经过检查完成出发作业驶出站点。如图1所示,上述列车或车厢在车站进行了一系列的技术作业过程,又可称为“到-解-集-编-发”过程。

图1 编组站的典型布置示意图
为更好地描述调机路径规划问题定义了一些相关概念,对调车场内所需要涉及的轨道进行分类,用来停放和存储车厢的轨道称为容纳轨道,该类轨道可分为来源轨道和集结轨道,来源轨道停放了各个去向的车厢,集合轨道集结了去向相同的车厢。根据需要移动车厢的相对位置,来源轨道又可分为直接轨道和间接轨道。
本文讨论了调机路径规划问题,通过调机将存放在不同来源轨道的车厢集中到集结轨道完成集结任务,目的是为调机寻找一条最短的移动路径。
本文以图2停留在调车场的小规模列车厢为例,颜色各异的方框代表去向各不相同的车厢,四边圆弧的方框表示调机,假设斜线方框代表去往目的地A的车厢,黑色方框代表去往目的地B的车厢,白色方框代表去往目的地C的车厢。所有车厢都连续性的停放在来源轨道而不是分散在任意轨道上,而且车厢移动必须通过调机来实现。

图2 单个调机问题示意图
根据图中车厢的初始位置可知,轨道2称为间接轨道,轨道3成为直接轨道,轨道4是集结轨道,现在要将去往目的地B的车厢即黑色方框代表的车厢聚集到集结轨道直到满足出发条件出站。而调机移动间接轨道的车厢时,要注意还要将去往另一个目的地A的车厢即斜线方框代表的车厢移回到原来的位置。换句话说,现在面临的问题就变成了寻找调机将黑色车厢聚集到集结轨道并将灰色车厢返回到原来的位置的最佳路径。
为了能更好地使用逻辑程序语言编码问题,根据文献[2]中转换网络图的方法,可以将图2中调车场的车厢初始位置图转换成网络图,那么该问题就变成了寻求符合约束条件的路径问题。在图3中,节点S表示调机的初始位置轨道,节点D表示直接轨道,节点B表示集结轨道,节点I1和I2都表示间接轨道且是同一条轨道,也就是说节点I2是节点I1的虚拟节点,目的是为了避免双向路径的存在,节点E表示结束轨道,箭头直线表示调机可以在这两轨道之间移动。
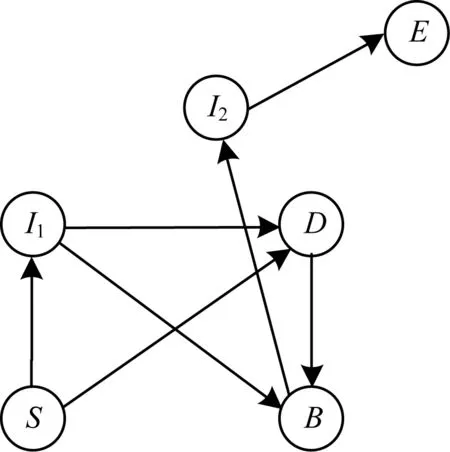
图3 网络图转换示意图
3 解决方案
3.1 ASP问题描述
借鉴文献[11]中用ASP对火车路径的编码方法,目的是为了得到符合规则的最短路径的回答集。定义的网络图是由一系列的节点和边组成的,节点代表轨道,边代表调机在两轨道间能进行移动。为了能更直观地描述网络图,本文定义下列谓词,如表1所示。

表1 ASP程序谓词及含义
上述所定义谓词以ASP规则形式给出相互之间的推导关系:
规则1node(X):-arc(X,Y)
规则2node(Y):-arc(X,Y)
由规则1可知节点是来源于边的,当存在一条边开始于X时,可推断出X是一个节点。规则R2类似。
规则3in(X,Y)v~in(X,Y):-arc(X,Y),reached (X)
由规则3可知如果存在一条边,调机会通过它的节点,那么这条边可能会成为回答集的一部分。因为存在从相同的节点出发的多条边的情况,而只有其中一条会成为最短路径的一部分。
规则4:-in(X,Y),in(X1,Y),X!=X1
规则5:-in(X,Y),in(X,Y1),Y!=Y1
由规则4可知在回答集中不可能有从同一个节点出发而在不同节点结束的两条边同时存在的情况。规则5类似规则4,但是将结束节点代替了开始节点。
规则6reached(Y):-in(X,Y)
由规则6可知当一条边成为最短路径的一部分时,调机一定会通过连接这条边的2个节点。
规则7reached(X):-start(X)
规则7可知最终得到的最短路径是必须通过指定的开始节点和结束节点。规则8就是适用于处理这2个特殊的节点,这是必要的规则。
规则8:-node(X),not reached(X)
为确保整个程序的运行过程能持续进行直到找出符合条件的回答集,其实也就是为了确保网络图中每个节点都被调机遍历一遍。规则8可以理解为求解出的回答集中不可能存在一个没有被调机所经过的节点X。
规则9~规则14是将调机所有可以移动的路径都表示出来:
规则9arc(X,Y):-start(X),a1(Y)
规则10arc(X,Y):-start(X),f2(Y)
规则11arc(X,Y):-a1(X),f2(Y)
规则12arc(X,Y):-f2(X),f3(Y)
规则13arc(X,Y):-a1(X),f3(Y)
规则14arc(X,Y):-a2(X),end(Y)
为得到切实的回答集答案,将节点用“a”“b”“c”“d”“e”代替,给以事实F1~F6:start(a)、f3(b)、f2(c)、a1(d)、a2(e)、end(f)。
3.2 CLP(FD)描述问题
这个方法描述了已设定的节点和边之间可能存在的最短路径。为更好地描述事实,引入了列表的概念,列表的元素由方括号括起。为了能更直观地描述网络图,定义下列谓词,如表2所示。
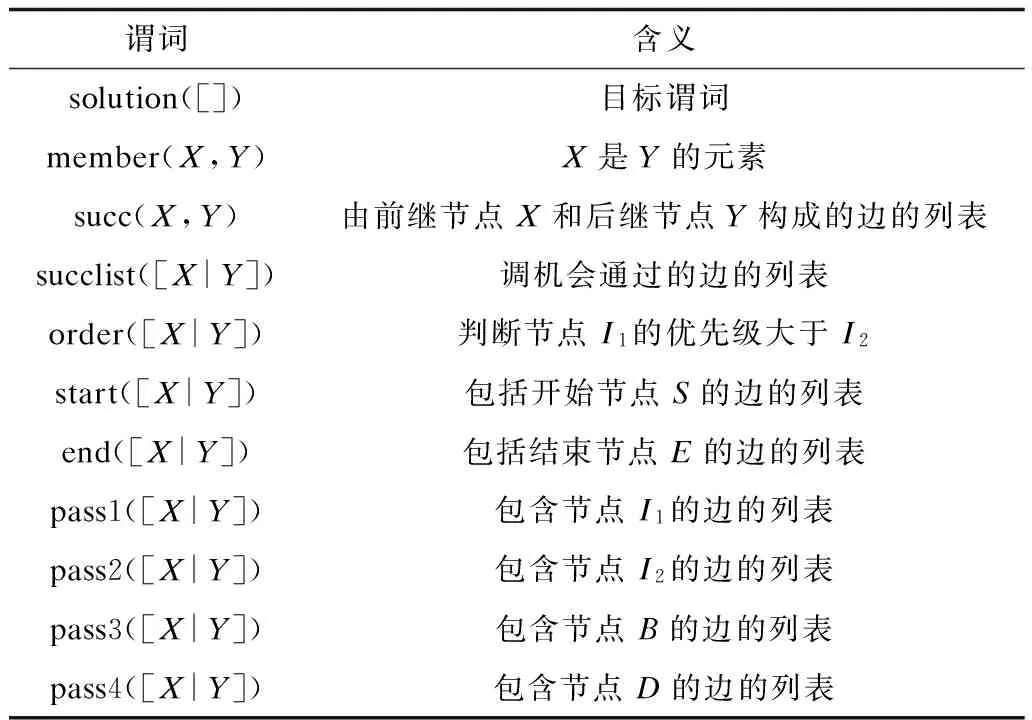
表2 CLP(FD)程序谓词及含义
上述所定义谓词以CLP(FD)规则形式给出相互之间的推导关系如下:
规则15solution(List):-succlist(List),start(List),end(List),pass1(List),pass2(List),pass3(List),pass4(Li st),order(List),domain(List,1,K),labeling([ff],List)
由规则15可知符合所有约束条件的列表。
规则16succ(Pre,Succ):-graph(Nodes,Edges),me mber(Pre,Nodes),member(Succ,Nodes),member([Pre,Succ],Edges
由规则16可知边由前继节点和后继节点构成。
规则17succlist([X,Y]):-succ(X,Y)
规则18succlist([X,Y|R]):-succ(X,Y),succlist ([Y|R])
由规则17、规则18可知从开始节点到结束节点的边必须形成通路,而且要遍历所有节点。
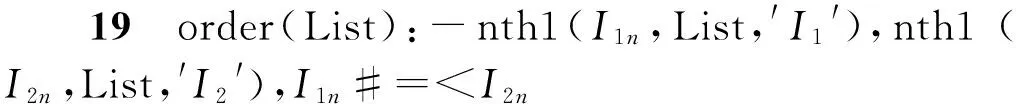
由规则19可知节点I1优先级比节点I2。相比而言,其他方法很难将这个约束条件简洁地表示出来。
规则20~规则30是将调机所有可以移动的路径表示出来:
规则20end([′E′|[]])
规则21end([_|T]):-end(T)
规则22start([′S′|_])

规则24pass1([_|T]):-pass1(T)

规则26pass2([_|T]):-pass2(T)
规则27pass3([′B′|_])
规则28pass3([_|T]):-pass3(T)
规则29pass4([′D′|_])
规则30pass4([_|T]):-pass4(T)
为更好地寻求答案,给予相对应的事实graph([‘S’,‘I1’,‘B’,‘D’,‘I2’,‘E’],[[‘S’,‘I1’],[‘S’,‘D’],[‘I1’,‘D’],[‘I1’,‘B’],[‘D’,‘B’],[‘B’,‘I2’],[‘I2’,‘E’]])。第1列列表代表节点,第2列列表表示节点之间存在的边。
4 实验结果与分析
4.1 运行结果
将ASP方法中的全部规则与事实输入到DLV求解器中得到的回答集如图4所示。

图4 ASP方法中得到的回答集
该回答集罗列了从开始节点到结束节点存在的最短路径。调机从节点S出发到达节点I1,然后移动车厢到达节点D,接着将要组成出发列车的车厢移动到节点B,最后将多余的车厢移回到原始轨道即节点I2,调机到达节点E标志着整个移动过程结束。
同样地,将CLP(FD)方法所编写的规则和事实输入到SWI求解器得到一个列表如图5所示。
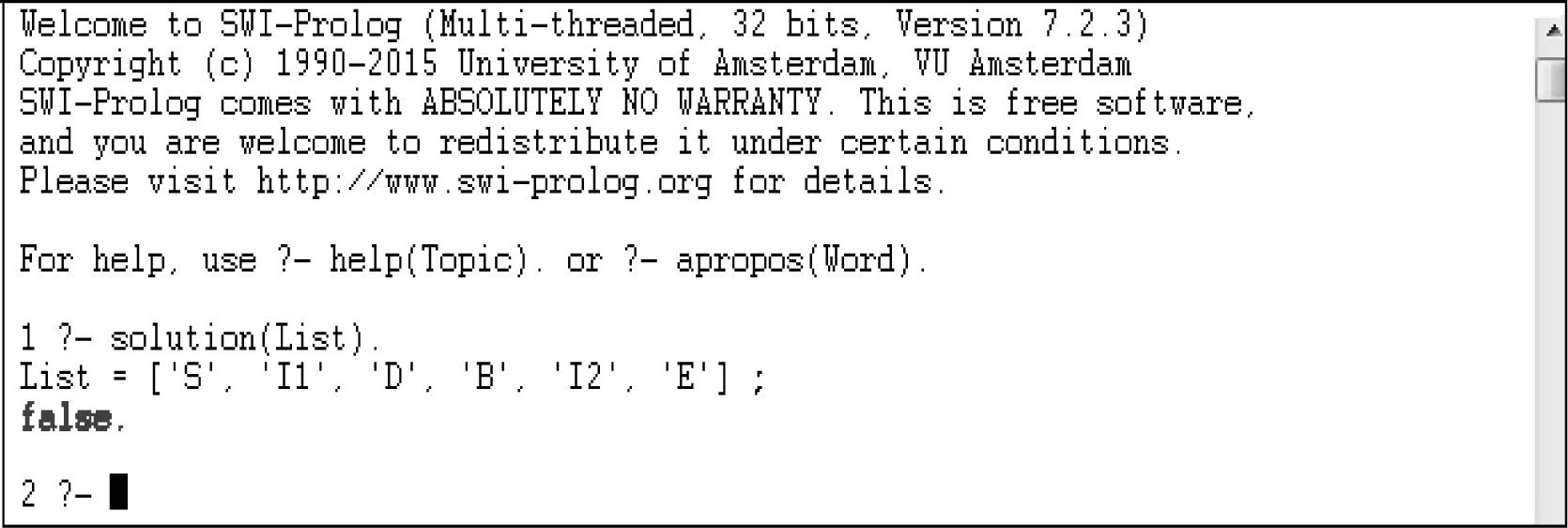
图5 CLP(FD)方法列表
根据该列表可得调机的移动路径,首先调机从节点S移动到间接轨道节点I1进行作业,然后再移动到直接轨道节点D接着移动到了集结轨道节点B,并将多余的车厢移动返回到原始的间接轨道节点I2,最后调机到达节点E完成所有的移动工作。
根据以上结果可知2种方法所得到的移动路径是一致的。结合图3可知调机不可能一次将所有去向相同的车厢移动到集结轨道,只能一次一次分步骤地将它们移动到集结轨道。分析上述运行结果可知调机的移动路径:
1)调机从初始位置移动到间接轨道;
2)将所有停放在间接轨道的车厢移动到直接轨道;
3)将所有黑色车厢包括在它之前已经停放在调车场的其他去向的车厢一起移动到集结轨道;
4)将其他去向的车厢移回到原始位置结束移动。
文献[2]也采用混合整数线性规划模型对该实例进行了讨论,并且采用了SimShunt仿真软件进行了验证,而本文所得的答案与其仿真结果也是一致的,说明逻辑程序能得到最优结果,并且证明了逻辑程序对解决该类问题是有效的。
4.2 比较实验
本节内容旨在寻求不同轨道数量大小下2种方法的求解效率,为今后实现调机运用计划的自动编制工作的方法选取奠定基础。以中国最大编组站之一的丰台西站为例,可知上行系统的调车场有30个股道,以此作为调车场轨道数的最大值进行实验。根据新添加规则的规律编写了如图6所示的程序随机产生器。
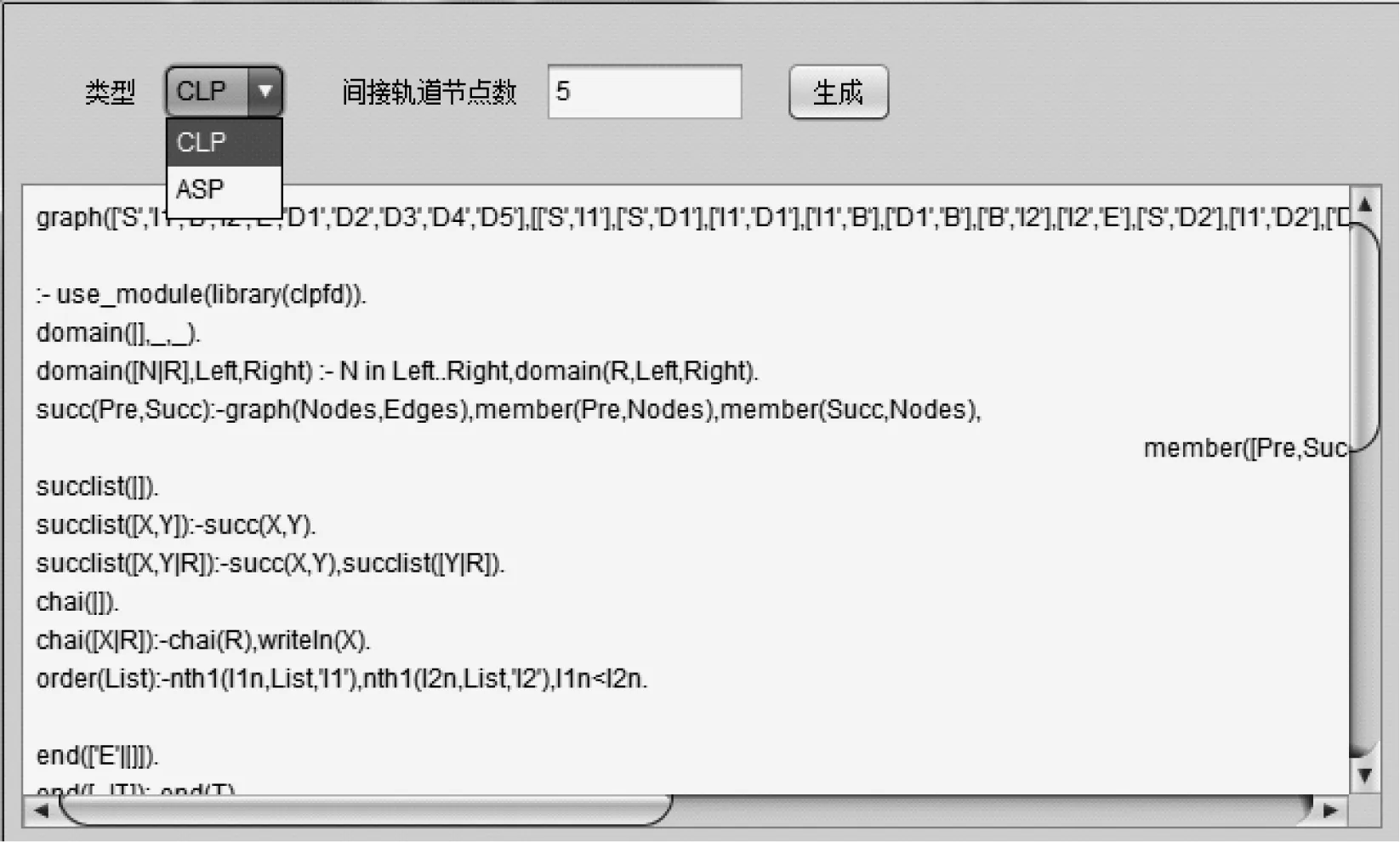
图6 程序随机产生器
图6中随机输入代表间接轨道的节点数,会产生相对应的程序规则。由于不同解决器效率并不相同,将选择多种求解器来运行程序。ASP程序要在求解器DLV和Smodels中运行,CLP(FD)也要在2种不同的求解器SWI和SICStus中运行。同一程序在不同求解器运行的语法会有差别,对于在Smodels和SICStus中运行的程序语法要根据各自的使用手册稍做修改。
程序在不同求解器的运行结果所表示的移动路径是一致的,但是运行时间各不相同,如表3所示。
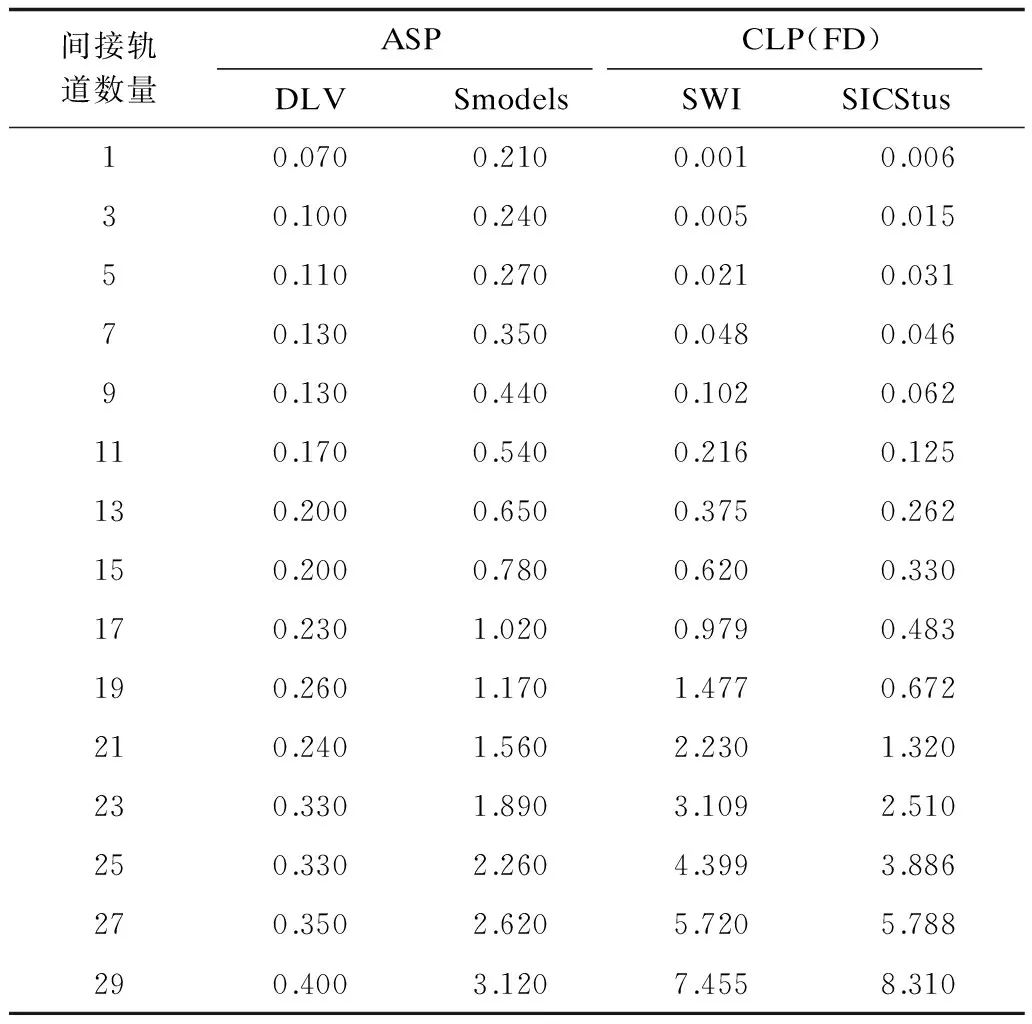
表3 不同运行程序运行时间 s
由图7可知:当间接轨道数增加时,不管是ASP程序还是CLP(FD)程序运行时间都有所增加,这是符合实际情况的。在间接轨数较小时,CLP(FD)程序在2种求解器的运行时间均比ASP程序的运行时间短,但随着轨道数不断增加,CLP(FD)程序运行时间反而骤然增加,远超过ASP程序的运行时间。反观ASP程序运行时间增长缓慢,增长率相比CLP(FD)程序低很多。对于运行ASP程序的两种解决器,DLV运行时间增加量极少,一直趋于稳定,增长率比Smodels低。由这些趋势可判断,当问题中轨道规模增大时,ASP程序在解决单个调机路径规划问题上比CLP(FD)有更好的表现,并且DLV求解器相比其他求解器更能有效地克服轨道数量增大带来的影响。

图7 求解器运行时间效率
5 结束语
针对各台编组调机移动路径的编排工作,本文分别给出基于ASP和CLP(FD)的逻辑程序设计方法,并结合实例分析了该方法能有效解决调机路径规划问题,实验结果表明,在此类问题的解决上ASP的运行时间比CLP(FD)短,ASP能更加快速地得到路径编排结果,在轨道数不断增多的情况下,DLV求解器相比其他求解器运行时间增长缓慢,趋于稳定,即DLV求解器比其他的求解器能更有效地克服轨道数目增减带来的影响。下一步将利用本文方法研究编组站单双向系统的多调机运行计划的编制问题。
[1] 黎浩东,何世伟,王保华,等.铁路编组站阶段计划编制研究综述[J].铁道学报,2011,33(8):13-22.
[2] ADLBRECHT J A,HUTTLER B,ZAZGORNIK J,et al.The Train Marshaling by a Single Shunting Engine Problem[J].Transportation Research Part C,2015,58:56-72.
[3] 赵 军,韩雪松,彭其渊.技术站配流与调机运用综合问题的拉格朗日松弛算法[J].铁道学报,2011,33(11):1-7.
[4] AHUJA S G,RAVINDRA K.Single-machine Scheduling with Stepwise Tardiness Costs and Release Times[J].Journal of Industrial and Management Optimization,2011,7(4):825-848.
[5] 徐 杰,杜 文,李宗平,等.基于模拟退火算法和图着色的调车机安排研究[J].铁道学报,2003,25(3):24-30.
[6] 王 烁,何世伟,黎浩东,等.禁忌搜索算法在编组站调机运用计划中的应用[J].铁道运输与经济,2011,7(1):76-79.
[7] 张瑞锋.基于混合算法的带时间窗的车辆路径问题求解[J].计算机工程,2007,33(14):185-187.
[8] BREWKA G,EITER T,TRUSZCZYNSKI M.Answer Set Programming at a Glance[J].Communications of the ACM,2011,54(12):92-103.
[9] FRIIHWIRTH T,HEROLD A,KIICHENHOFF V,et al.Constraint Logic Programming——An Informal Introduction[C]//Proceedings of the 2nd International Logic Programming Summer School.Zurich,Switzerland:[s.n.].1992:1-35.
[10] BOENN G,BRAIN M,de V M et al.Automatic Music Composition Using Answer Set Programming[J].Theory and Practice of Logic Programming,2011,11(2/3):397-427.
[11] ADLBRECHT J A,HUTTTLER B,ILO N,et al.Train Routing in Shunting Yards Using Answer Set Programming[J].Expert Systems with Applications,2015,42(1):7292-7302.
[12] 徐成刚,易军凯,肖 洋.基于约束逻辑程序设计的排课算法研究[J].计算机工程与应用,2006,42(31):197-199.
[13] LEONE N,PFEIFER G,FABER W,et al.The DLV System for Knowledge Representation and Reasoning[J].ACM Transactions on Computational Logic,2006,7(3):499-562.
[14] 党华锐,郑守淇.约束逻辑程序设计综述[J].计算机科学,1994,21(4):11-14.
[15] 常万军,郭祖华,魏昆鹏.约束逻辑程序的良基模型研究[J].计算机工程,2013,39(9):298- 302.
