模拟矿岩散体的PFC细观参数标定方法

刘 欢 任凤玉 何荣兴 李广辉(东北大学资源与土木工程学院，辽宁 沈阳 110819)

PFC(Particle Flow Code)属于离散单元法，是一种适用于解决非连续性问题的数值方法，它仅由颗粒之间的微观参数来表现各种材料的宏观力学行为[1]。由于PFC可用来模拟矿岩散体的运动、旋转以及散体间相互作用等非线性行为，目前已被广泛地应用于研究矿岩散体的各项力学行为以及采矿工艺中。

王培涛等[2-3]借助PFC研究了无底柱分段崩落法的相关放矿规律，得出颗粒间摩擦系数越大放出椭球体的偏心率越大，并且研究了炮孔边孔角与端壁所受侧压力的关系；程爱平等[4]应用PFC模拟了金山店铁矿低贫化放矿工艺，证明在金山店推行低贫化放矿方法完全可行；孙浩等[5-6]应用PFC研究了复杂边界和多放矿口条件下崩落矿岩流动特性，表明在复杂边界以及多放矿口条件下放出体形态会产生不同程度的变异，并不是一个规则的椭球体；邹晓甜等[7]研究了溜井底部放矿漏斗角对矿石流动性的影响，分析不同放矿漏斗角下的矿石流动性特征，揭示了放矿漏斗角对矿石流动性的影响机理；井伯祥等[8]研究了覆盖层中散体颗粒的移动规律，研究表明覆盖层内小颗粒的平均速度大于大颗粒的速度，且进路上方的颗粒速度较快。这些研究均表明，PFC较好地解决了与采矿有关的各种矿岩散体问题，然而PFC 的原理是通过设置每个接触的本构模型实现对材料宏观性质的模拟，如何恰当选择颗粒间的接触本构模型以及模型中的细观参数，使PFC中颗粒的性质与矿岩散体的性质相匹配，对于研究矿岩散体的各种力学行为将有重要的意义。

1 PFC接触本构模型

PFC的基本原理是采用介质最基本单元(颗粒)、最基本的颗粒运动法则(牛顿第二定律)以及颗粒间的接触本构模型来描述介质的复杂力学行为。不同颗粒间通过接触点处的力和力矩产生相互作用，在特定条件下不断更新颗粒间的接触力和力矩，并通过离散元的方法计算系统的时间演化，从而为牛顿运动方程提供了一种显式的动态解决方案。颗粒间接触本构模型体现了接触颗粒之间的力学特征并控制着颗粒间相互作用力和力矩的更新。因此，能正确反映矿岩散体的性质，需要选择合理的接触本构模型及其细观参数。目前PFC提供了9种接触本构模型，其中常用来模拟无黏连矿岩散体的接触本构模型有3种，分别为Line Model(线性接触模型)、Hertz Contact Model(赫兹接触模型)和Rolling Resistance Linear Model(抗转动线性接触模型)。当然PFC也允许用户自定义接触本构模型来实现材料的宏观本构性质。

矿岩散体由大量的非均匀岩块组成，这些岩块很难被定量地描述其几何形态，虽然PFC也可以通过Clump(颗粒簇)将小颗粒组合在一起形成不同形状的岩块或将颗粒直接黏结在一起形成岩块，但去描述这些岩块的几何形态以及形成如此大量的矿岩散体均不太现实，同时这也会极大地降低计算机的计算速度，尤其当颗粒数目很庞大时模拟极有可能失真。但在离散元方法中可以用滚动摩擦系数的大小来模拟颗粒的形状[9]，PFC提供的众多接触本构模型中，Rolling Resistance Linear Model(抗转动线性接触模型)[10]增加了抗转动系数，原理是在接触点上增加了与接触颗粒间相对转动时呈线性增加的内力矩，这会降低颗粒的转动能力，其与非均匀岩块的性质极其接近。因此，在模拟矿岩散体时推荐采用抗转动线性接触模型或是将线性接触模型、赫兹接触模型和抗转动线性接触模型组合应用分别赋予不同性质的散体颗粒。抗转动线性接触模型的力-位移方程为

Fc=Fl+Fd,

(1)

Mc=Mr,

(2)

式中，Fc为颗粒所受到的接触力，N；Mc为接触力矩，N·m；Fl为线性接触力，N；Fd为阻尼力，N；Mr为抗转动力矩，N·m。

在模拟计算过程中随着颗粒的运动，线性接触力与阻尼力随着颗粒间法向与切向接触位移量的改变而更新，抗转动力矩随着颗粒间相对转动增量的变化而更新。抗转动线性接触模型中细观参数主要包括颗粒的有效模量E*，法向和切向刚度比k*，摩擦系数fric，抗转动系数rr_fric。

2 矿岩散体物理力学性质标定方法

矿岩散体的物理力学性质主要包括散体的密度、块度及级配、内摩擦角和黏聚力，其中散体的密度、块度及级配可以直接设定具体值，散体的内摩擦角和黏聚力可以借助数值剪切试验直接获得，也可以间接通过放出体或自然安息角的大小来反映散体的力学性质。

2.1 数值剪切试验

剪切试验是测定松散矿岩内摩擦角和黏聚力的常用方法，在已知矿岩散体内摩擦角、黏聚力以及剪切位移与剪切应力变化曲线时，可以借助数值剪切试验将接触本构模型中细观参数与矿岩散体的物理力学性质参数相匹配，PFC剪切试验如图1所示。然而由于矿岩散体的平均块度较大，目前常规的剪切试验装置并不能测定矿岩散体的内摩擦角和黏聚力，因此通过数值剪切试验标定接触本构模型中细观参数的方法具有一定的局限性。

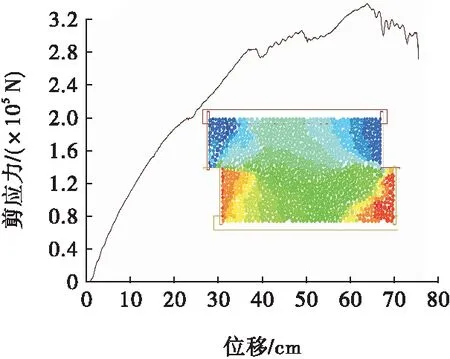
图1 PFC剪切试验Fig.1 Shearing test of PFC

2.2 放出体数值试验

放出体可以间接反映散体的物理力学性质，放矿过程中矿岩移动的产物就是放出体。放出体是指从出矿口放出的矿石在采场崩落矿岩堆体中原来占有空间位置所构成的形体[11]。放出体的形态与大小反映着矿岩的移动规律以及散体的流动能力，是散体物理力学性质的一个综合指标。因此可以通过数值放矿试验，将获得的放出体形态和大小与实际放出体相比较，当一致时即可将接触本构模型中细观参数与矿岩散体的物理力学性质参数相匹配[6]，PFC放出体试验如图2所示。目前，关于测定放出体的试验均是在试验室内获得，Castro R等[12]虽然进行了较大模型的放矿试验，但与实际采场放矿还有一定的差距。因此研究放矿的基本规律时可应用该方法，但研究采矿现场问题时该方法并不适用。

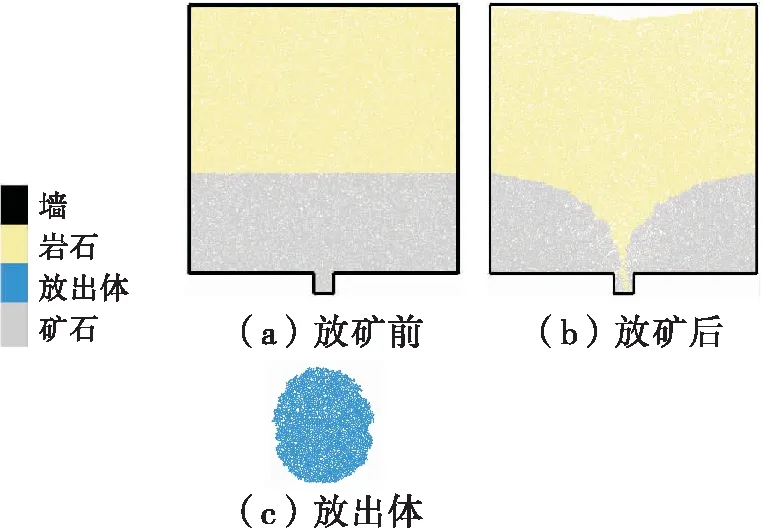
图2 PFC放出体试验Fig.2 Test of PFC drawn-out ore body

2.3 自然安息角数值试验

自然安息角是指自然湿度下的松散矿岩，在某一特定条件下堆积，其自然坡面和水平面所形成的最大倾角[13]。自然安息角是松散矿岩颗粒间摩擦角、黏聚力和重力平衡的一个重要标志，同时自然安息角也是试验室模拟矿岩散体与现场矿岩散体力学相似的准则[13]。因此通过自然安息角数值试验，当测得的值与实际自然安息角相同时，即可将接触本构模型中细观参数与矿岩散体的物理力学性质参数相匹配。然而对于同一种矿岩散体使用不同的测定方法时，测得的自然安息角也存在差异，需要依据实际的测定条件、测定方法或采矿方法来建立与之匹配的数值模型。根据不同的测定条件，可建立如下几种数值模型。

(1)有静压力，无边壁的影响。该条件下常采用圆筒式测定装置测定散体的自然安息角，因此建立的数值模型如图3所示。测得的自然安息角可用来标定卸矿场、废石场中散体的物理力学性质。

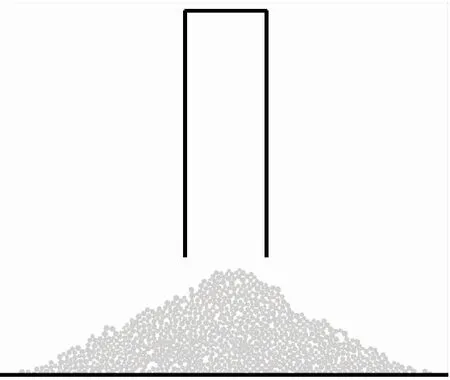
图3 PFC圆筒测定试验Fig.3 Cylinder measurement test of PFC

(2)有静压力，有边壁的影响。该条件下常采用载压式测定装置测定散体的自然安息角，建立的模型如图4所示。其中关于压力的模拟可借助PFC伺服控制系统控制顶部墙体与颗粒间的接触力，以此来模拟施加的压力。测得的自然安息角可用来标定有底柱采矿法、无底柱采矿法以及留矿采矿法(大量放矿的初期)中散体的物理力学性质。

图4 PFC载压测定试验Fig.4 Pressure measurement test of PFC

(3)无静压力，有边壁的影响。该测定条件下常采用旋转式测定装置测定散体的自然安息角，建立的数值模型如图5所示。测得的自然安息角可用来标定空场采矿法、留矿采矿法(大量放矿的后期)中矿岩散体的物理力学性质。

图5 PFC旋转测定试验Fig.5 Rotating measurement test of PFC

(4)有滚动和滑动摩擦力的影响。该测定条件下采用塌落式测定装置，建立的数值模型如图6所示。测得的自然安息角可用来标定矿仓、溜井中散体的物理力学性质。

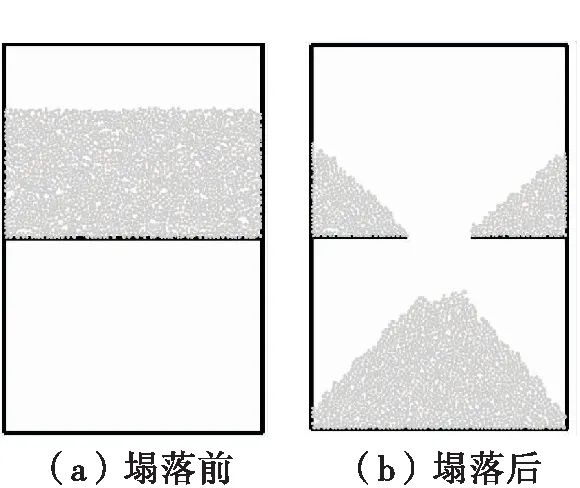
图6 PFC塌落式测定试验Fig.6 Caving measurement test of PFC

综上所述，在标定接触本构模型的细观参数时，推荐采用与测定条件相符合的自然安息角数值试验。由于PFC接触模型中接触的类型包括颗粒与颗粒以及颗粒与墙之间的接触，故采用数值旋转式模型来研究PFC接触本构模型的细观参数对散体自然安息角的影响。

3 矿岩散体细观参数的标定

抗转动线性接触模型中有效模量E*与岩石颗粒的变形指标弹性模量有关，并且随着弹性模量的增加而增加，法向和切向刚度比k*与岩石的泊松比有关，这2个参数可通过相关的力学试验获得。在其他参数一定时，通过调整摩擦系数fric和抗转动系数 rr_fric完成模拟矿岩散体的PFC细观参数标定。数值旋转式模型如图5，模型尺寸为200 mm×400 mm，颗粒的半径为1～3 mm、3～5 mm、5～7 mm、7～10 mm且所占的体积份数分别为55%、25%、15%、5%，密度为2 700 kg/m3，有效模量为1.0×107Pa，法向和切向刚度比为1.0。

3.1 摩擦系数

分别考虑颗粒的摩擦系数与墙的摩擦系数对自然安息角的影响，摩擦系数选取0.1、0.3、0.5、0.7、0.9，抗转动系数为0.2。结果绘制成摩擦系数与自然安息角关系曲线(如图7所示)。由图7可知，随着颗粒或墙的摩擦系数的增大，自然安息角均呈现出先增大后基本稳定的趋势，但颗粒的摩擦系数对自然安息角有较显著的影响。

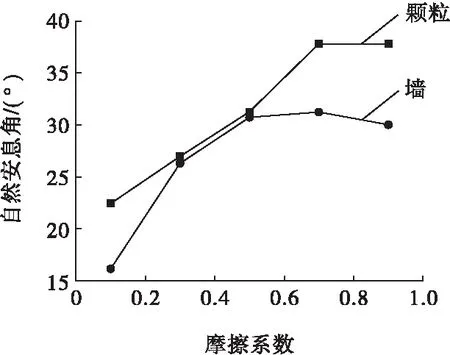
图7 摩擦系数与自然安息角的变化曲线Fig.7 Curve of the friction coefficient with the repose angle

3.2 抗转动系数

分别考虑颗粒的抗转动系数与墙的抗转动系数对自然安息角的影响，抗转动系数选取0.0、0.2、0.4、0.6、0.8，摩擦系数为0.4。结果绘制成抗转动系数与自然安息角关系曲线(如图8所示)。由图8可知，随着颗粒或墙的抗转动系数的增大，自然安息角均呈现出先增大后基本稳定的趋势，但颗粒的抗转动系数对自然安息角有较显著的影响。

3.3 摩擦系数和抗转动系数

为了进一步研究摩擦系数与抗转动系数对自然安息角的影响，分别选取颗粒的摩擦系数为0.1、0.3、0.5、0.7、0.9，抗转动系数为0.2、0.4、0.6，保证墙的摩擦系数和抗转动系数不变，模拟结果详见图9。由图9可知，随着颗粒的摩擦系数和抗转动系数的增大，自然安息角呈增长的趋势，且不同的摩擦系数与抗转动系数组合可以获得相同的自然安息角。图9中自然安息角的范围从22°～50°，与实际松散矿岩自然安息角相符。

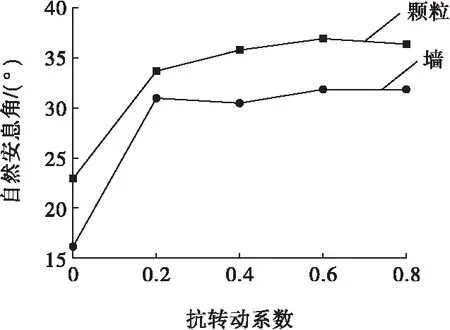
图8 抗转动系数与自然安息角的变化曲线Fig.8 Curve of the rolling resistance coefficient with the repose angle

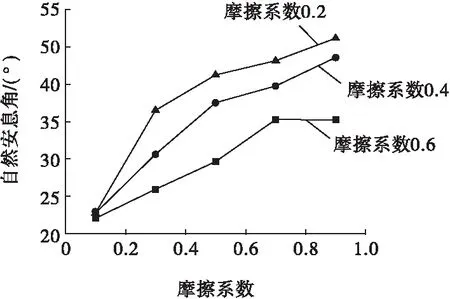
图9 抗转动系数和摩擦系数对自然安息角的影响Fig.9 Influence of rolling resistance coefficient and friction coefficient on the repose angle

4 结 论

(1)根据PFC接触本构模型并结合矿岩散体本身的特点，提出采用抗转动线性接触模型或将抗转动线性接触模型、线性接触模型以及赫兹接触模型组合应用分别赋予不同性质的散体颗粒。

(2)阐述了数值剪切试验、放出体数值试验以及自然安息角数值试验的优缺点，推荐采用与测定条件相符合的自然安息角数值试验来标定PFC细观参数。

(3)通过自然安息角数值试验分别研究了抗转动线性接触模型中颗粒及墙的摩擦系数和抗转动系数与散体自然安息角的关系。研究表明：随着颗粒或墙的摩擦系数和抗转动系数的增加，自然安息角均呈现出先增大后趋于稳定的趋势，且颗粒的摩擦系数和抗转动系数对自然安息角有较显著的影响。

(4)模拟结果中自然安息角的变化范围为22°～50°，与实际松散矿岩自然安息角相符。

[1] 张社荣，孙 博，王 超，等.双轴压缩试验下岩石裂纹扩展的离散元分析[J].岩石力学与工程学报，2013，32(S2)：3083-3091.

Zhang Sherong，Sun Bo，Wang Chao，et al.Discrete element analysis of crack propagation in rocks under biaxial compression[J].Chinese Journal of Rock Mechanics and Engineering，2013，32(S2)：3083-3091.

[2] 王培涛，杨天鸿，柳小波.无底柱分段崩落法放矿规律的PFC2D模拟仿真[J].金属矿山，2010(8)：123-127.

Wang Peitao，Yang Tianhong，Liu Xiaobo.PFC2D numerical simulation of ore drawing rule with pillarless sublevel caving[J].Metal Mine，2010(8)：123-127.

[3] 王培涛，杨天鸿，柳小波.边孔角对无底柱分段崩落法放矿影响的颗粒流数值模拟研究[J].金属矿山，2010(3)：12-16.

Wang Peitao，Yang Tianhong，Liu Xiaobo.Particle flow numerical simulation investigation on influence of lateral opening angle on ore drawing with sublevel pillarless caving[J].Metal Mine，2010(3)：12-16.

[4] 程爱平，许梦国，王 平.金山店铁矿低贫化放矿数值模拟[J].金属矿山，2011(1)：31-34.

Cheng Aiping，Xu Mengguo，Wang Ping.A numerical simulation of low dilution ore drawing in Jinshandian Iron Mine[J].Metal Mine，2011(1)：31-34.

[5] 孙 浩，金爱兵，高永涛，等.复杂边界条件下崩落矿岩流动特性[J].中南大学学报:自然科学版，2015，46(10)：3782-3788.

Sun Hao，Jin Aibing，Gao Yongtao，et al.Flow characteristics of caved ore and rock under complex boundary conditions[J].Journal of Central South University:Science and Technology，2015，46(10)：3782-3788.

[6] Jin A B，Sun H，Ma G W,et al.A study on the draw laws of caved ore and rock using the discrete element method[J].Computers and Geotechnics，2016，80：59-70.

[7] 邹晓甜，刘艳章，张丙涛，等.溜井底部放矿漏斗角对矿石流动性的影响研究[J].金属矿山，2016(12)：160-164.

Zou Xiaotian，Liu Yanzhang，Zhang Bingtao，et al.Research on effect of drawing funnel angle at the bottom of ore-pass on ore fluidity[J].Metal Mine，2016(12)：160-164.

[8] 井伯祥，陈 超，张亚宾，等.覆盖层颗粒移动规律的PFC2D数值模拟[J].金属矿山，2016(6)：43-48.

Jing Boxiang，Chen Chao，Zhang Yabin，et al.PFC2D numerical simulation in velocity law of covering layer particles[J].Metal Mine，2016(6)：43-48.

[9] Wensrich C M，Katterfeld A.Rolling friction as a technique for modelling particle shape in DEM[J].Powder Technology，2012，217：409-417.

[10] Kazuyoshi I，Masanobu O.Rolling resistance at contacts in simulation of shear band development by DEM[J].Journal of Engineering Mechanics，1998，124(3)：285-292.

[11] 刘兴国.放矿理论基础[M].北京：冶金工业出版社，1995.

Liu Xingguo.Base of Ore-drawing[M].Beijing：Metallurgical Industry Press，1995.

[12] Castro R，Trueman R，Halim A.A study of isolated draw zones in block caving mines by means of a large 3D physical model[J].International Journal of Rock Mechanics and Mining Sciences，2007，44(6)：860-870.

[13] 周 骥.对松散矿石自然安息角的研究[J].有色金属，1983，35(2)：24-29.

Zhou Ji.An investigation on angles of natural repose of bulk ores[J].Nonferrous Metals，1983，35(2)：24-29.