不同拓扑结构原棉品质指标预测模型的预测效果对比
2018-01-18,,,,
,,, ,
(1.塔里木大学机械电气化工程学院,新疆阿拉尔 843300;2.浙江盛元化纤有限公司,杭州 311247;3.巴州纤维检验所,新疆库尔勒 841000;4.东华大学机械工程学院,上海 201620)
当前,中国的棉花加工技术仍较为落后,主要体现在轧花模式单一(如以单一轧花速度轧制不同品质籽棉[1]),人工经验判别轧花质量,尚未采用在线监测与调控生产状况。在轧花过程中,棉花轧制质量的优劣受多种因素影响(如棉花性状、温湿度、轧花速度、喂花量、加工机械等),且人工很难对各影响因素进行有效调控[2-4]。国内外研究者采用田口鲁棒设计法、模糊控制和智能专家系统控制策略等非线性方法,分析轧花过程中轧花参数与原棉品质的关系[5-7],取得了良好效果。BP神经网络预测方法可有效建立因变量与自变量间的非线性关系,其在处理工业、农业生产的各类非线性因果参数领域展现卓越的效果[8-9]。经前期20型轧花机轧花品质实验室试验研究,发现采用BP神经网络及其衍生方法可有效预测原棉轧花品质[10-11]。因工业生产场所与实验室内试验环境存在本质差异,且前期研究多为多因素对单一指标预测分析,未能实现多指标对多指标的预测。
为此,本文以南疆库尔勒地区产手摘陆地棉为原料,选库尔勒尉犁县某轧花厂为试验场地,从轧花生产实践的关键因素籽棉回潮率、轧花速度和喂花量为因变量,建立轧花原棉的上半部平均长度(upper half mean length,UHML)、强度(strength,Str)和短纤指数(short fiber index,SF)的3个品质指标预测模型。在实践生产条件下,分析手摘籽棉脱籽后原棉的3个品质指标预测有效性,为后期轧花品质在线控制奠定实践基础。
1 建模准备
1.1 材料与仪器
试验选用新疆库尔勒市尉犁县新中陆37手摘籽棉。
MY-96型锯齿轧花机(山东天鹅棉业机械有限公司),台时籽棉加工量600~1 200 kg/h,电机功率45 kW,转速820 r/min(实测);Y421-B型原棉水分测定仪(南京思欧仪器有限公司),回潮率测量范围4%~15%,分辨率0.01%;DT2234C智能数字转速表(深圳市欣宝瑞仪器有限公司),测量范围2.5~999.99 r/min,分辨率0.1 r/min,有效测距范围50~500 mm;PTI-G通用变频器(广州保瓦科技有限公司),适配功率45 kW,电源相数3相,额定电压380 V。
1.2 轧花流程
试验轧花样品提取于库尔勒市尉犁县某棉业有限公司2#车间。该车间轧花工艺流程如图1所示。

图1 轧花工艺流程
1.3 轧花试验
以籽棉回潮率、轧花速度、喂花量3个轧花参数为变量,轧制原棉的HVI指标(HUML、Str和SF)为原棉品质评价指标,建立多因素试验。在前期试验研究发现,轧花垛场内籽棉随棉花空气温湿度变化,故按时段(依据前期试验在24 h内取5个时段,3、9、14、19、23时作为不同回潮率籽棉提取轧制时间段)用原棉水分测定仪测量提取于皮清机后管道内棉样的回潮率。由轧花锯齿滚筒至皮清机后端管道内,原棉随气流运行过程极短,近似认定管道内原棉回潮率为籽棉轧花时的回潮率。轧花机的轧花速度由变频器调节轧花机锯齿滚筒转速,并利用数字转速表校对变频器调节后锯齿滚筒实际转速。锯齿轧花机的锯齿滚筒电机频率由变频器控制调节,锯齿辊筒转速计算见式(1)。
n=820f/50
(1)
式中:n为锯齿辊筒转速;f为试验设置调频器频率。试验设置变频器调频依次为35、38、40、45、50 Hz。轧花机喂花量由人工在轧花控制台调控单位时间喂花量。
多因素试验参数如表1所示。轧花试验按表1中3个关键因素量值进行多因素试验设置(试验每次调节轧花速度和喂花量后,待轧花机运行稳定后再提取试样)进行试验。为提高试验样品的准确与稳定性,每组试验提取原棉样品10次。将不同试验参数下所轧制原棉送至库尔勒纤维检测所,采用乌斯特HVI1000型大容量棉纤维测试仪检测试验样品的品质指标(UHML、Str、SF)。各试验样本原棉测试10次,取10次测试值的算术平均值为试验各指标的样本数据。

表1 多因素试验参数指标
2 BP神经网络模型算法与拓扑结构
BP神经网络算法由非线性单元组成,是一种前馈式学习算法与反向传播算法的神经网络[12],广泛用于非线性函数逼近、模式识别和数据预测等领域。
梯度下降法和牛顿迭代法是BP神经网络模型最为主要的算法。梯度下降法最初下降速度快,接近目标值时梯度下降缓慢,误差函数下降缓慢,易陷入局部极小,而牛顿迭代法可克服此弊端[13]。梯度下降法和牛顿迭代法相结合形成了Levenberg-Marquardt算法(L-M算法),此算法比其他算法的迭代次数少、收敛速度和精度都高。故本文BP神经网络算法采用L-M算法。
BP神经网络拓扑结构由输入层、隐含层和输出层组成。BP神经网络的隐层结构指隐层层数和隐层的神经元个数,其对BP神经网络学习性能影响颇大,往往研究者依据经验公式设定,不易得到最佳值而影响BP神经网络性能。
在理论分析中,典型的3层BP网络已能够映射或逼近任何有理函数[14],故BP神经网络结构设计通常采用1个隐含层的BP神经网络。部分研究者表明,多隐含层BP神经网络的自学、泛化能力更强且预测效果更精确[15]。然BP神经网络拓扑结构层数的增加也致使网络结构复杂化,增加了BP神经网络权值的训练时间。故在处理简单的映射关系时,在保证满足预测精度时可选3层BP网络结构;在处理复杂的映射关系时可选3层以上的BP网络结构。
隐含层节点数目往往采用Kolmogorov定理进行确定,Kolmogorov定理[16]如下:
任意连续函数f:
Un→Rm,f(X)=Y
(2)
式中:U为闭单位区间[0,1];f为3层目标网络。
对于BP神经网络,隐含层层数为1,节点数为2n+1(n指输入节点数。);隐含层层数大于1,每隐含层节点数<2n+1,各隐含层节点总数≤2n+1。
3 实验样本数据
在不同籽棉回潮率、轧花速度和喂花量3个自变量下,轧花多因素试验所采集的手摘原棉品质指标(UHML、Str、SF)数据共计30组,如表2所示。

表2 手摘原棉品质指标样本数据
注:*为测试样本。
由表2可知,其中前3项(实测回潮率、轧花速度和喂花量)为网络模型学习样本的输入层自变量,后三项(HVI大容量棉纤维测试仪检测的UHML、Str、SF品质指标)为输出层因变量。选1~25组测试数据作为BP神经网络训练样本数据,建立BP神经网络模型。取26~30组数据作为验证数据,检测BP神经网络的预测能力。
4 BP神经网络模型结构设计与优化
选原棉回潮率、轧花速度和喂花量3个关键因素为网络的输入,选HIV检测原棉的UHML、Str、SF指标为网络的输出,依据Kolmogorov定理确定隐含层节点数,建立原棉单一品质指标的BP神经网络预测模型。
3层网络拓扑结构的隐含层传递函数为tansig,输出层传递函数为purelin,训练函数为trainlm(Levenberg-Marquardt算法),学习速率为0.05,目标误差为1×10-5,最大训练迭代为12 000次。4层网络拓扑结构的隐含层传递函数依次为tansig、tansig,输出层传递函数为purelin,训练函数为trainlm,学习速率为0.05,目标误差1×10-5,最大训练迭代为9 000次。5层网络拓扑结构的隐含层传递函数依次为tansig、tansig、logsig,输出层传递函数为purelin,训练函数为trainlm,学习速率为0.05,目标误差1×10-5,最大训练迭代为11 300次。
BP神经网络训练前,为增强原棉各品质指标数据差异显著性,各关键因素的数据均进行归一化,原棉品质各数据值均减去其绝对值数值最大的值作为输出值。
依据Kolmogorov定理设计网络拓扑结构,发现3层网络结构1种,4层网络结构21种,5层网络结构33种。以表2内的轧花数据为基础数据,建立相应预测模型,经试算得出模型目标值与预测值的相关系数,如表3所示。
比较表3内不同网络结构的模型相关系数,发现3-7-3、3-5-2-3和3-3-2-2-3网络结构模型的相关系数R均比同类拓扑结构的值大,分别为0.973 4、0.943 6和0.984 1,其值均约等于1。
原棉品质指标预测模型效果最佳的3、4、5层网络拓扑结构BP网络拓扑结构分别确定为3-7-3、3-5-2-3和3-3-2-2-3,网络结构如图2—图4所示。3-7-3、3-5-2-3和3-3-2-2-3网络拓扑结构的BP神经网络模型训练样本回归直线,如图5—图7所示。图5—图7中,纵坐标Y为网络测试输出值,是轧花品质预测模型(BP神经网络模型)训练后计算所得的指标值;横坐标X为网络测试目标值,是轧花品质预测模型训练后所要达到的目标值。即3-7-3、3-5-2-3和3-3-2-2-3网络拓扑结构模型的回归直线与斜率为1的直线(Y=X)基本相吻合。由此表明,3-7-3、3-5-2-3和3-3-2-2-3网络拓扑结构的轧花品质预测模型对MY-96型轧花机进行轧花品质预测均很有效。

表3 不同拓扑结构模型相关系数

图2 BP神经网络模型拓扑(3-7-3)
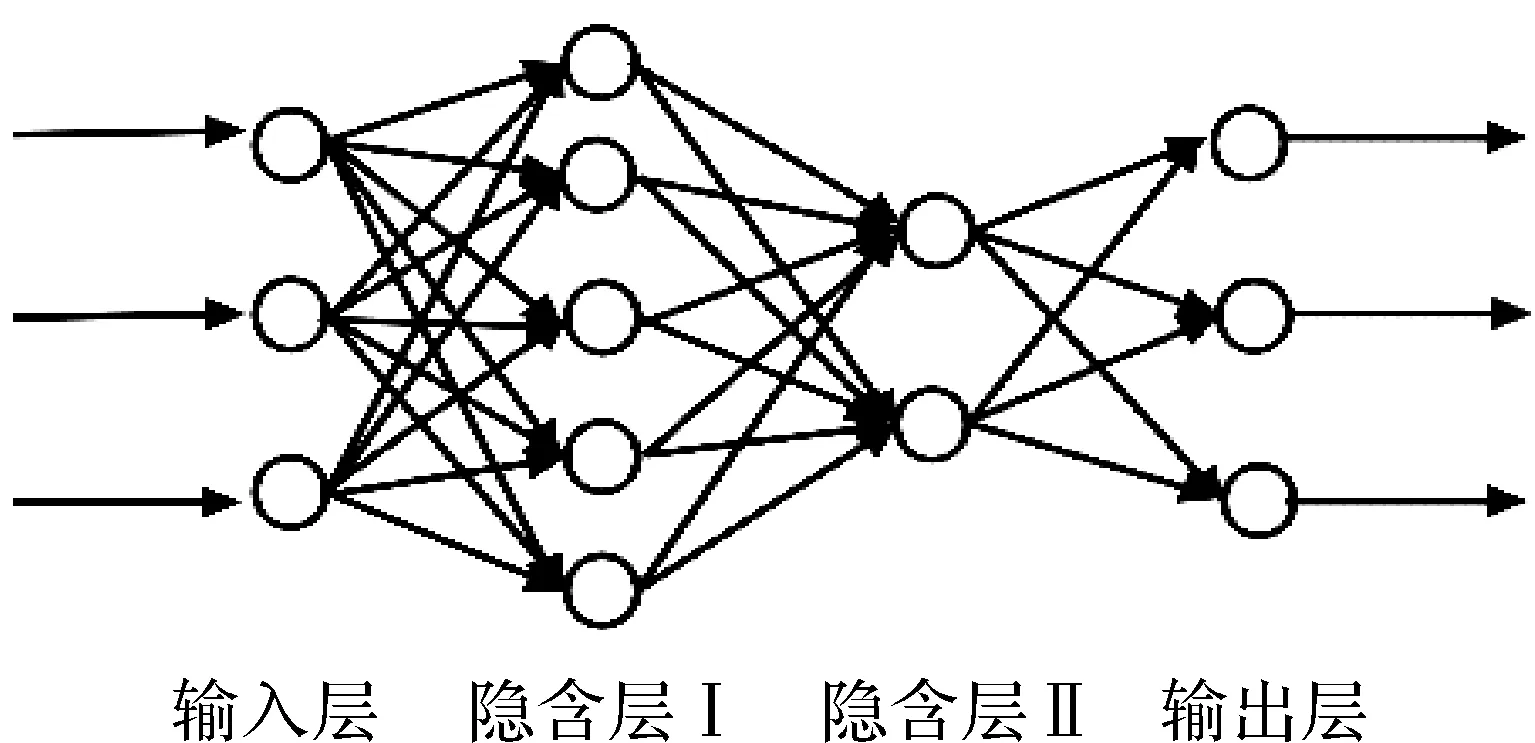
图3 BP神经网络模型拓扑(3-5-2-3)

图4 BP神经网络模型拓扑(3-3-2-2-3)

图5 3-7-3模型训练样本输出回归直线

图6 3-5-2-3模型训练样本输出回归直线

图7 3-3-2-2-3模型训练样本输出回归直线
采用均方根误差(MSE)特征指标进行比较3种网络结构的预测效果,各网络结构预测模型的MSE指标,见表4。由表4可知,3-3-2-2-3网络拓扑结构的BP神经网络模型的拟合效果要优于3-5-2-3和3-7-3网络拓扑结构的BP神经网络模型的拟合效果。

表4 不同BP网络拓扑结构预测模型仿真结果误差对比
5 预测效果验证
3-3-2-2-3网络拓扑结构的BP神经网络对手摘原棉的品质指标进行验证,手摘原棉UHML、Str、SF指标估测值与实测值对比,见图8。由图8可知,手摘原棉UHML、Str、SF的模型估测值与试验实测值极为相近。由此表明,3-3-2-2-3网络拓扑结构的BP神经网络对轧花厂轧花机的轧花原棉品质可实现有效预测。
6 结 论
选库尔勒某手摘籽棉轧花厂为生产实践试验场,选择籽棉回潮率、轧花速度和喂花量3个关键因素作为输入层自变量,建立3个轧花品质指标(UHML、Str、SF)的预测模型。对比不同网络结构预测模型的预测效果,发现3-3-2-2-3网络拓扑结构的BP神经网络测模型效果最佳,该网络结构预测模型的预测输出值与试验目标值的相关系数达0.984 1。运用BP神经网络模型可实现籽棉轧花品质指标的有效预测。此方法研究开发于手摘籽棉轧花原棉品质在线监控软件开发。

图8 3-3-2-2-3网络结构的手摘棉品质指标预测值与实测值对比
[1] 张成梁.棉花加工过程智能化关键技术研究[D].济南:山东大学,2011.
[2] 袁志清.世界各主要产棉国棉花品质分析及适纺性研究[D].石家庄:河北科技大学,2013.
[3] 张兆峰,欧阳光红,徐炳琴.机采棉的性能特征及纺纱试验[J].棉纺织技术,2005,33(3):21-24.
[4] 王敏.机采棉清理加工工艺试验研究[D].兰州:甘肃农业大学,2009.
[5] HOLT G, LAIRD W. Screen for optimal operating parametersfor the powered roll gin stand using taguchi’s robustdesign[J]. Engineering and Ginning,2007,11(1):79-90.
[6] 董全成,冯显英.基于自适应模糊免疫PID的轧花自动控制系统[J].农业工程学报,2013,29(23):30-37.
[7] 王少林,茅忠明,伍贻文.棉花加工自动控制系统的设计[J].农业机械学报,2002,33(1):54-56,59.
[8] 胡雪棉,赵国浩.基于Matlab的BP神经网络煤炭需求预测模型[J].中国管理科学,2008(S1):521-525.
[9] 李惠军,朱磊.基于BP人工神经网络的纱线毛羽预测研究[J].棉纺织技术,2011,39(1):32-34.
[10] 李勇,陈晓川,汪军,等.基于BP神经网络的机采原棉品质指标预测模型[J].棉纺织技术,2015,43(1):17-20,56.
[11] 李勇,陈晓川,汪军,等.基于BP神经网络的原棉短纤指数预测模型[J].纺织学报,2014,35(8):36-40.
[12] 刘厚林,吴贤芳,王勇,等.基于BP神经网络的离心泵关死点功率预测[J].农业工程学报,2012,28(11):45-49.
[13] 胡昌军.双隐层BP神经网络模型在区域水安全评价中的应用[J].水资源与水工程学报,2013,24(3):196-200.
[14] 郑绪枝,雷靖,夏薇.基于快速确定隐层神经元数的BP神经网络算法[J].计算机科学,2012,39(6):432-436.
[15] 王泽平.基于GA-BP与多隐层BP网络模型的水质预测及比较分析[J].水资源与水工程学报,2013,24(3):154-160.
[16] 赵振宇,徐用懋.模糊理论和神经网络的基础与应用[M].北京:清华大学出版社,1996.
