HXD2型机车制动缸死区输入自适应补偿

崔 晶，谢程程，王桂荣

（1.西安铁路职业技术学院 牵引动力学院，西安 710026；2.中铁七局集团西安铁路工程有限公司 试验检测分公司，西安710026；3.中国计量大学 机电工程学院，杭州 310018）

0 引言

HXD2型电力机车基础制动装置采用单侧、双闸瓦、带闸瓦间隙自动调整器的独立踏面制动单元。

闸瓦间隙自动调整器（俗称闸调器）能根据闸瓦间隙的变化，通过调整螺母和引导螺母的配合，保证闸瓦与车轮的间隙正常[1]。当机车制动时，闸调器受到来自于制动缸的压力，推动高摩合成闸瓦与轮对踏面进行直接接触，并能够控制闸瓦与轮对踏面的接触程度，以逐渐增大摩擦力的方式实现能耗制动。在制动缸活塞杆的行程范围内，闸调器可确保机车制动力不衰减[2]。

高压气体流经细长的管路和管路弯折、接头及开口处所产生的沿程阻力和局部阻力会形成接触表面粘滞和局部压差而导致气压波动[3,4]。同时，理论研究中假想为绝对圆形的轮对踏面在实际工况中由于车体静载荷及机车通过钢轨接头、道岔和不平顺路段时所引起的踏面冲击载荷而在径向被压缩，折算为轮对轴向周期性形变量，致使轮对纵向及垂向加速度增大，制动时闸瓦与轮对踏面接触效果变差，并导致闸调器及闸瓦被反向挤压，甚至会影响其可靠性和使用寿命[5]。因此，管路内气压的波动干扰、轮对形变和踏面冲击成为影响制动缸闸调器及闸瓦位置是否得以精准控制的重要因素。

除过提升闸瓦的制作工艺和摩擦效能，实现高精度、高动态性能的闸瓦位置控制，防止其与轮对踏面过分接触，则需要精确控制制动缸活塞所受风压。在实际制动系统中，换向阀负责切换气路开闭，其开度的大小决定压力气体的流速。然而，由于换向阀需克服静态摩擦及残存的气压摄动方能移动，因此常发生阀口游移和润滑层磨损；此外，阀口处摩擦力较高而应变刚度较低，容易引发阀轴扭转导致静态工作点偏移，阀口导通发生时间滞后于系统的控制输入，此时会出现机械滞后现象（俗称死区），即阀口已经发生位移，但是对应的气路还未导通致使输入量不能进入系统产生作用[6]。因此风源压力此时不能进入制动缸，闸瓦位置移动发生时滞。只有当控制器的输出量足以克服死区的跳变范围，系统才会切换到正常的工作模式。

工程实际中，常通过采用机械精加工的办法削弱死区范围，最大程度上减小过程偏差度，但受制于机械结构和制造精度，死区难以全部消除。因此，需结合控制理论进一步提升具有死区输入的闭环伺服系统的工作效能，补偿死区非线性。其中，文献[7]采用微分自适应律估计未知死区参数，采用饱和函数代替符号函数消除颤振，利用鲁棒方法消除有界误差项，实现误差有界收敛，使得系统对期望目标的跟踪渐进稳定。文献[8]利用自适应模糊逻辑系统的万能逼近特点，在线逼近机电齿隙伺服系统中的未知参数和非线性环节，并引入齿隙近似死区函数避免死区函数的不可微，设计了鲁棒控制项抑制建模误差的影响，实现闭环伺服系统的有界跟踪。

然而，上述两种控制器的设计并未考虑换向阀阀芯游移方向不确定所引发的传动问题。制动状态下，死区效应会使得阀口行程误差增加，导通时间滞后，导致阀口所受气压冲击较为猛烈，阀芯因此产生颤振，虽然此颤振不至于影响机车制动，却导致其游移方向产生不确定性。同时，机车制动缸某些标称参数会因外界条件变化而发生时变和漂移，其内壁与活塞的接触面并非严格配合，导致内部压力漏损。

针对上述制动缸闸瓦位置控制系统中存在的标称参数漂移及内泄漏、轮对径向周期性形变干扰和阀芯因气压冲击产生颤振而游移导致控制方向不确定以及因工作点偏移而产生死区的实际工况，结合虚拟反馈控制律具有较强的误差收敛效果，同时考虑Nussbaum增益对控制方向不确定的系统具有较好的控制能力的特点，本文采用基于虚拟反馈的Nussbaum增益自适应控制对机车制动缸闸瓦位置控制系统的控制器进行设计，使得系统在制动工况下输出信号快速精确跟踪给定值的同时，亦能够克服内部参数漂移和外部压力波动干扰。

1 制动缸气动伺服系统建模

为推导具有死区输入的制动缸气动伺服系统的数学模型，特做假设如下：

1）供气压力连续，不计气体外泄漏；

2）不计气体局部、沿程能量损失；

3）流经伺服阀节流孔的气体绝热，气体比热和节流孔流量系数一定；

4）制动缸内气体热力学呈等温变化[9]，且不计阀口温漂；

5）滚珠丝杠传动系数一定；

6）闸瓦位移量及其各阶导数连续有界。

经简化后的HXD2机车制动系统如图1所示。可知，制动状态（1YA）时，制动管与大气连通排风减压，副风缸与制动缸连通，使制动缸活塞受压下移；缓解状态（2YA）时，制动管向副风缸充风，制动缸与大气连接，活塞在复位弹簧的作用下上移。换向阀伴随机车制动与缓解而往复切换于制动工位和缓解工位，楔形装置放大制动缸活塞的位移量，通过控制调整螺母的转动圈数控制滚珠丝杠螺杆的位移量：制动状态，调整螺母顺时针转动，螺杆推动活塞杆连动闸瓦向轮对踏面移动；缓解状态，调整螺母逆时针转动，螺杆带动活塞杆连动闸瓦远离轮对踏面。

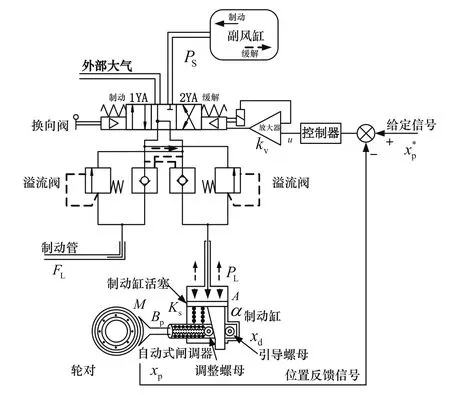
图1 HXD2机车制动系统简化

根据文献[10]，机车制动缸阀口死区模型如下：

式中，m为死区斜率，Br和Bf为死区切换点，xv为伺服阀阀芯位移。

由图1可知，HXD2机车制动缸为非对称阀控缸，其气体流量连续性方程为：

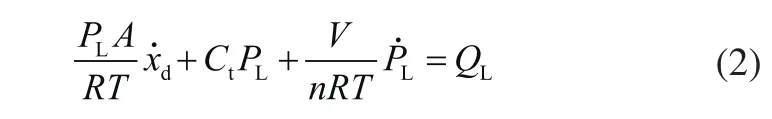
式中，A为活塞作用面积；R为气体常数；T为气体绝对温度；PS为副风缸供气压力；PL为制动缸作用压力；Ct为气体内泄漏量；V为气缸内腔体积；n为气体多变指数；xd为制动缸活塞位移。

制动缸活塞运动学方程为：

式中，A，PL定义同上；M为活塞及闸瓦质量；Bp为黏性阻尼系数；Ks为活塞等效弹性负载系数，FL为风压波动干扰。

伺服阀阀口流量方程为：

式中，Cd为阀口流量系数；w为阀口面积梯度；xv为阀芯位移量，为气体密度。

楔形放大机构模型为：

式中，xd为制动缸活塞位移；α为楔角角度；ϕ为螺母转角，d0为调整螺母中径。

滚珠丝杠传动模型为：

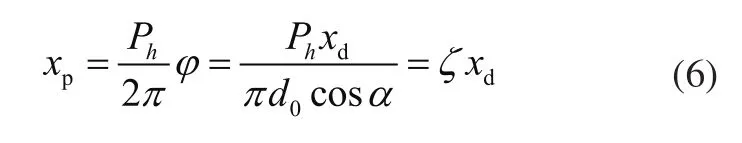
伺服阀增益方程为：

式中，kv＞0为伺服阀放大器增益系数，u为电压控制输入；xv为伺服阀阀芯位移。

依据上述分析，建立机车制动缸闸瓦位控系统等效气动伺服数学模型如下：

式中，控制量前的“±”表示阀口游移方向。

2 自适应控制器设计

定义跟踪误差为：

设计虚拟反馈控制函数为：

式中，c1，c2均为非负的待设计参数。

设计自适应控制器如下：

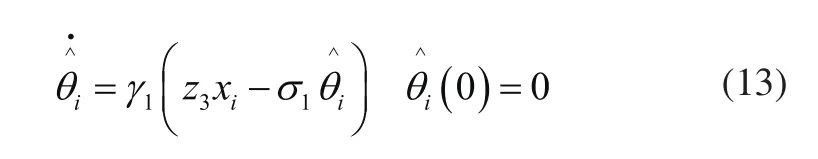
3 闭环稳定性分析

引理1[12]： 设V(t)在上连续，k(t)在上连续可微，且对设N(k)是偶的光滑的Nussbaum类型函数，θ为非零常数。若对有：

定义Lyapunov候选函数如下：

对上式求导，并带入式(10)至式(14)后可得：

参照不等式：

可知：

将上式进一步转化，并整理可得：

式中：

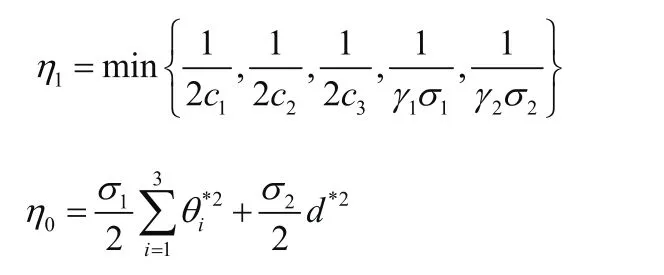
对式(20)两边同时乘以emt，并对t积分可知：

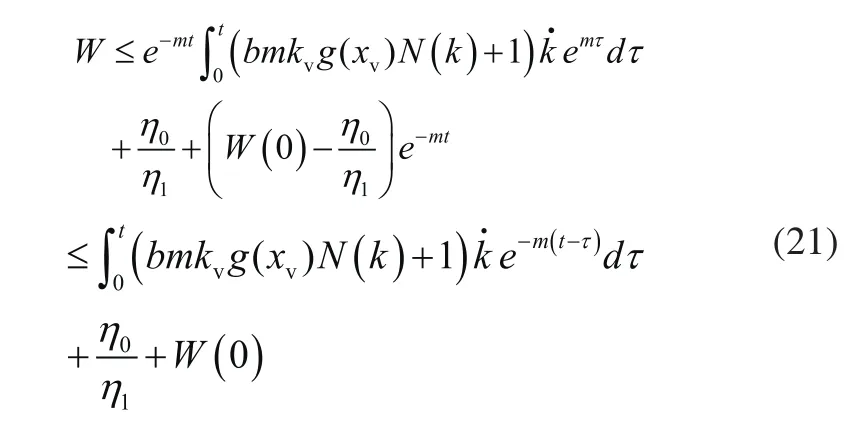
由引理1可推知：

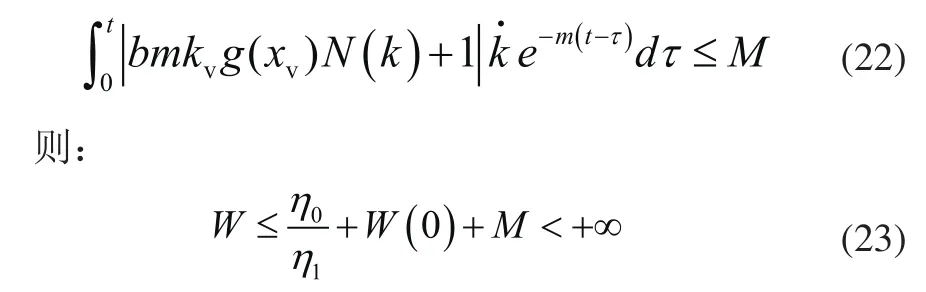
由Babalat引理可知，W有界并收敛，结合式(16)可得，闭环系统所有信号z1、均为半全局一致终结有界并收敛于0[13,14]。

4 仿真结果及分析

对制动缸闸瓦位置控制系统分别采用基于虚拟反馈控制律的自适应控制器（VFAC）和模糊PID控制器进行仿真研究，所得到的闸瓦位置指令跟踪曲线如图2所示。

考虑实际系统输入存在延迟，并非直接阶跃跳变，而是以指数形式趋近于稳态，故设定信号输入为：

式中，xs=1mm；tr=0.02s。

考虑管路中存在的压力波动、踏面冲击以及承受轮对挤压的压力摄动，定义外界时变压力扰动及因系统工作点变化所引起的内部参数摄动分别为：

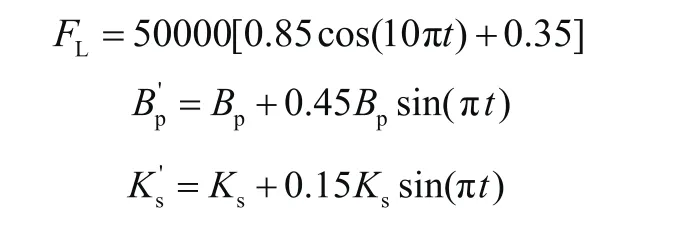
制动缸闸瓦位置控制系统标称参数如表1所示。

表1 制动缸闸瓦位置控制系统参数标称值

由图2、图3可知，采用模糊PID的位置控制系统虽然能够根据模糊规则的变化较为有效抑制扰动影响，但上升时间内由于模糊控制规则较为固定，使输出滞后，跟踪效果不佳（上升时间长达0.2s，跟踪误差最大接近0.33mm，恢复跟踪时间接近0.2s）；而VFAC由于针对干扰和参数时变而设计，控制器设计过程中遵循Lyapunov稳定性原理，故可确保系统稳态无超调，有效抵消参数摄动和外界较大扰动的影响，形成近似无偏跟踪；其误差曲线在历经上升时间及调整时间后迅速收敛至0（跟踪误差最大接近0.002mm，恢复跟踪时间接近0.1s），表明其对应的输出量已恢复跟踪输入量。由图4、图5可知，相比于模糊PID依据模糊规则不断调整致使控制输入存在抖振，VFAC由于对参数自适应估计，且能够抑制扰动及未建模动态对控制量的影响，使控制输入在零点附近切换平滑无抖振，且较模糊PID控制输入曲线（用时0.12s）更为迅速收敛于零状态（用时0.05s），其正向和负向控制所对应的Nussbaum类型函数均一致有界并收敛，说明系统在仿真时间内可以达到一致渐进稳定状态。

综上所述，制动缸闸瓦位置控制系统具备较强鲁棒性，可有效克服外界压力扰动和内部参数摄动，对输入指令实现近似无偏跟踪。

图2 位置输入指令跟踪曲线

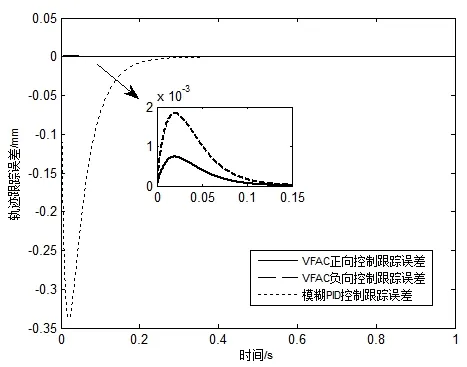
图3 位置跟踪误差曲线

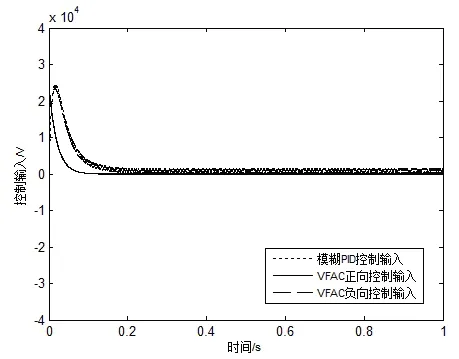
图4 控制量输入曲线

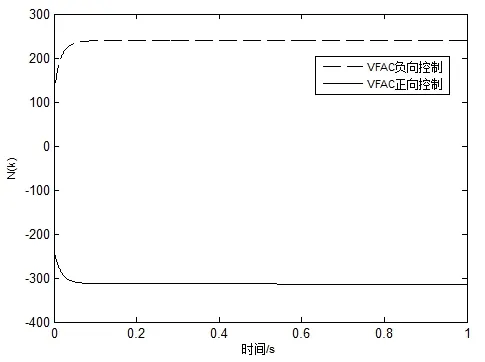
图5 Nussbaum函数曲线

5 结论

本文针对HXD2型电力机车制动缸闸瓦位置控制系统中换向阀阀芯因颤振而游移导致控制方向未知以及因工作点偏移导致输出响应滞后而引发死区输入的实际工况，引入Nussbaum类型函数，设计了一种基于虚拟反馈控制律的自适应控制器；设计了针对系统工作点变化所引起的内部标称参数摄动的参数自适应律；设计了针对轮对径向周期形变干扰的参数自适应律。

由推理和仿真结果知，本文所设计的控制器具有优点如下：

1）可以实现双向传动控制，系统输出能够在有限时间内实现快速收敛，具有较强的鲁棒性；

2）能够抑制系统内部的参数摄动和外界线路激扰;具备良好的动态特性，对输入指令可实现近似无偏跟踪。

如何将本文理论研究成果与实际应用相结合是下一步研究的重点。

[1]李益民,马金法,黄志高.交流电力机车制动系统[M].成都:西南交通大学出版社,2014.

[2]崔晶,张省伟.电力机车总体及走行部[M].成都:西南交通大学出版社,2016.

[3]马艳玲,黄进,张丹.基于反步自适应控制的伺服系统齿隙补偿[J].控制理论与应用,2008,25(6):1090-1094.

[4]Joe H, Kim M,Yu S. Second-order sliding mode control for autonomous underwater vehicle in the presence of unknown disturbances[J].Nonlinear Dynamics,2014,78(1):183-196.

[5]Lin K J. Sliding mode control design for uncertain singular systems[J].Applied Mechanics and Materials,2012,14(5):16-20.

[6]马艳玲.含齿隙环节伺服系统的补偿控制[D].西安:西安电子科技大学,2008.

[7]朱胜,孙明轩,王雪洁,等.具有输入死区的非线性系统的鲁棒重复控制[J].自动化学报,2013,39(6):908-912.

[8]杜仁慧,吴益飞,陈威,等.电液伺服系统的非线性鲁棒自适应控制[J].控制理论与应用,2013,30(02):254-260.

[9]訚耀保,荒木献次.具有非对称气动伺服阀的气动压力控制系统建模与分析[J].中国机械工程,2009,20(17):2107-2111.

[10]郭健,姚斌,吴益飞,等.具有输入齿隙的一类非线性不确定系统自适应鲁棒控制[J].控制与决策,2010,25(10):1580-1584.

[11]许衍泽.具有输入饱和的轧机电液伺服系统多模型切换自适应控制研究[D].秦皇岛:燕山大学,2014.

[12]Ge S S, Hong F, Lee T H. Adaptive neural control of nonlinear time-delay system with unknown virtual control coefficients[J]. IEEE Trans.on Systems, Man and Cybernetics,2004,34(1):499-516.

[13]刘棕成,董新民,薛建平,等.一类不确定执行器非线性系统的自适应控制[J].系统工程与电子技术,2015,37(1):163-168.

[14]朱胜,孙明轩,何熊熊.输入具有齿隙非线性特性的周期系统的自适应控制[J].控制理论与应用,2012,29(04):535-538.