卫星轨道跟踪系统的设计

万敏辉，朱庆生，薛华建

（1.中科院南京天文仪器研制中心，南京 210042；2.中国科学院大学，北京 100039；3.中科院南京天文仪器有限公司，南京 210042）

0 引言

人卫激光测距系统的主要任务是精确测量激光脉冲的往返时间，其原理是望远镜上的激光发射机发出激光脉冲到达卫星，然后由卫星上的激光反射器反射回到接收机/探测器，根据发送接收的时间差计算得到卫星距地面的距离。因此望远镜能否准确跟踪卫星直接影响接收机/探测器的接收，从而影响激光测距的准确性。

目前，望远镜控制方法和控制策略一般采用位置PID控制算法[1,2]，或者根据位置误差范围发送设置的不同等级的恒动速度的控制方法[3]。这些控制方法一般用于跟踪恒星，对于不同高度下、速度变化快的卫星目标，达不到高精度的跟踪要求。为了准确地、高精度地跟踪卫星，本文提出了一种多项式拟合插值与前馈补偿的PID控制算法相结合的卫星轨道跟踪方法方法，其跟踪稳定性、高效性在项目——“中国科学院测量与地球物理研究所1米人卫激光测距望远镜”中得以验证。

1 卫星轨道跟踪系统设计

1.1 望远镜闭环检测系统

在项目“1米人卫激光测距望远镜”中，望远镜采用Copley驱动器控制直流伺服电机驱动的方案。赤经赤纬的位置采集装置为RENESHAW光栅编码器，采集到的位置信息分别反馈给赤经赤纬的Copley驱动器和主控计算机。

Copley驱动器内嵌电流环与速度环。电流环完全在驱动器内部进行，通过霍尔装置检测驱动器给电机的各相的输出电流，负反馈给电流环PID控制器，进行调节达到输出电流尽量等于设定电流。

速度环中，编码器反馈的值经过差分运算得到直流电机的速度，速度引导值与直流电机反馈的速度值之差作为速度控制器的输入，环内PID输出直接就是电流环的设定。

上位机负责望远镜的坐标计算和位置检测，然后向驱动器发送速度控制命令，构成位置环，环内的PID输出直接就是速度环的设定，形成三环控制的卫星轨道跟踪系统。望远镜的闭环检测系统如图1所示。

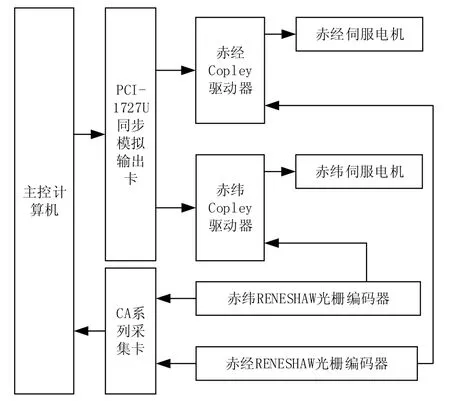
图1 望远镜的闭环检测系统

调节Copley驱动器中电流环与速度环PID参数至合适值，分别给望远镜方位轴和俯仰轴发送5°/s和2°/s速度控制命令，两轴实际响应曲线如图2所示。根据编码器读取的位置数据计算可知，望远镜方位轴速度在18760角秒/秒上下波动，俯仰轴速度在7300角秒/秒上下波动，均存在稳态误差，此误差对卫星跟踪的影响可由上位机软件中的位置环控制消除。

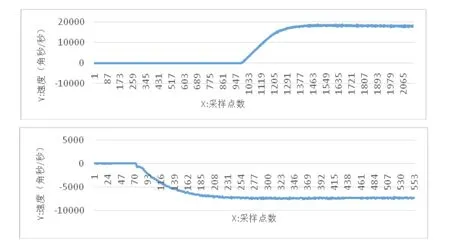
图2 望远镜方位轴5°/s，俯仰轴2°/s的速度响应曲线

1.2 位置环闭环跟踪控制程序设计

在三环控制的卫星轨道跟踪系统中，位置环为三环控制的最外环，位置环内PID的输出为速度环的设定。位置环由主控计算机与实时反馈望远镜位置的编码器构成。目的为根据卫星轨道位置与编码器反馈的望远镜实际位置，计算发送的速度，保证望远镜能够实时指向卫星。以下为主控计算机中位置环闭环跟踪控制的详细设计过程，图3为主控计算机内位置环程序设计框图。

首先，软件读取卫星轨道引导文件。实验中，卫星轨道引导数据文件由国家天文台编写的星历预报软件PreTLE V3.0_for ali[4]获得，软件根据在celestrak网站（http：//celestrak.com/NORAD/elements）下载的Tle数据文件、包含测站地理位置的测站数据文件以及预报参数文件可生成观测引导文件。观测引导文件中包含卫星编号，日期、时间（世界时），测站地平系下的卫星方位角，高度角等信息，且数据率为1Hz。

然后通过GPS获取测站的实时时间t，如果t大于卫星起始坐标时间t0，则望远镜开启位置环跟踪的多媒体定时器，望远镜开始跟踪。否则望远镜定位到起始坐标位置，等待t＞t0条件的满足。

当条件t＞t0满足，开启位置环跟踪多媒体定时器的同时，读取计数卡PCI-TMC12计数值count0。在回调函数中，先读取计数卡PCI-TMC12计数值count1，由于计数卡晶振为800kHz，每一个计数代表1.25×10-6s，则跟踪时长为T=(count1-count0)1.25×10-6s，根据轨道引导文件，插值计算（t0+T）时刻的卫星坐标，同时读取此时刻望远镜方位俯仰读数，经增量式PID算法计算得到较前一时刻速度的偏差量，向望远镜发送计算后的速度控制命令。如果T不大于（t1-t0），即望远镜跟踪卫星·过程未结束，程序重复调用回调函数。否则关闭位置环跟踪多媒体定时器，卫星跟踪结束。

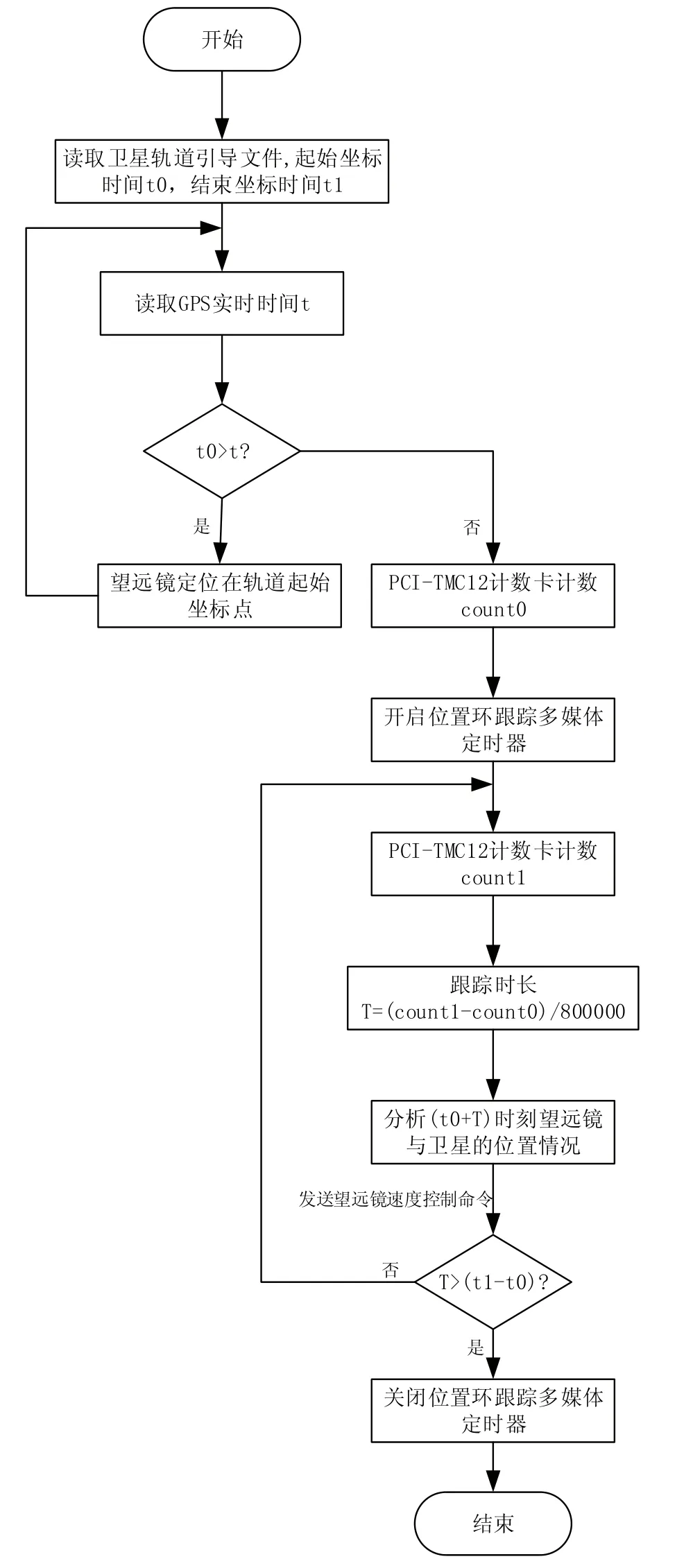
图3 卫星轨道跟踪系统位置环程序设计框图

在整个卫星轨道跟踪系统中，关键是计算任一时刻卫星坐标的准确性以及消除位置误差的快速性。

2 多项式系数求解法

插值算法的优劣决定了跟踪时卫星实时位置坐标的精确度。常用的插值算法有拉格朗日多项式插值[5]，牛顿多项式插值[6,7]以及内维尔逐次线性插值等。每种插值方法的插值阶数阶数过大时，插值精度反而会下降[6]。在插值阶数选取合理的情况下，每种插值算法的插值误差量级都很小，在精度要求范围内，各种算法均是可行的。但在高采样率的情况下，对各种插值算法的计算时间进行比较，多项式系数求解法的效率最高[8]。

多项式系数求解法的定义：对于n次多项式：

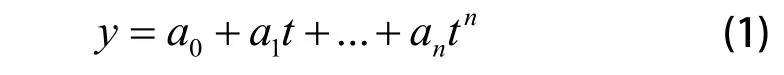
轨道引导文件给出的卫星位置时间间隔为1s，计算插值误差时，取5s间隔的卫星位置作为内插点，内插计算各个内插时间段中间时刻的卫星位置，并将内插得到的卫星位置同原轨道文件的卫星位置进行比较。在内插过程中，为了提高插值精度，尽量将插值点位置选在节点的中间[9]。以3轨高纬轨道（俯仰最大高度均大于70°）为例，计算各阶数下的插值误差结果，单位为角秒，实验结果如表1、表2所示。

分析表1，表2的实验数据可知，当阶数为7阶时，方位俯仰的内插平均误差均小于0.1''。则根据式(1)，卫星的轨道的插值方程为：

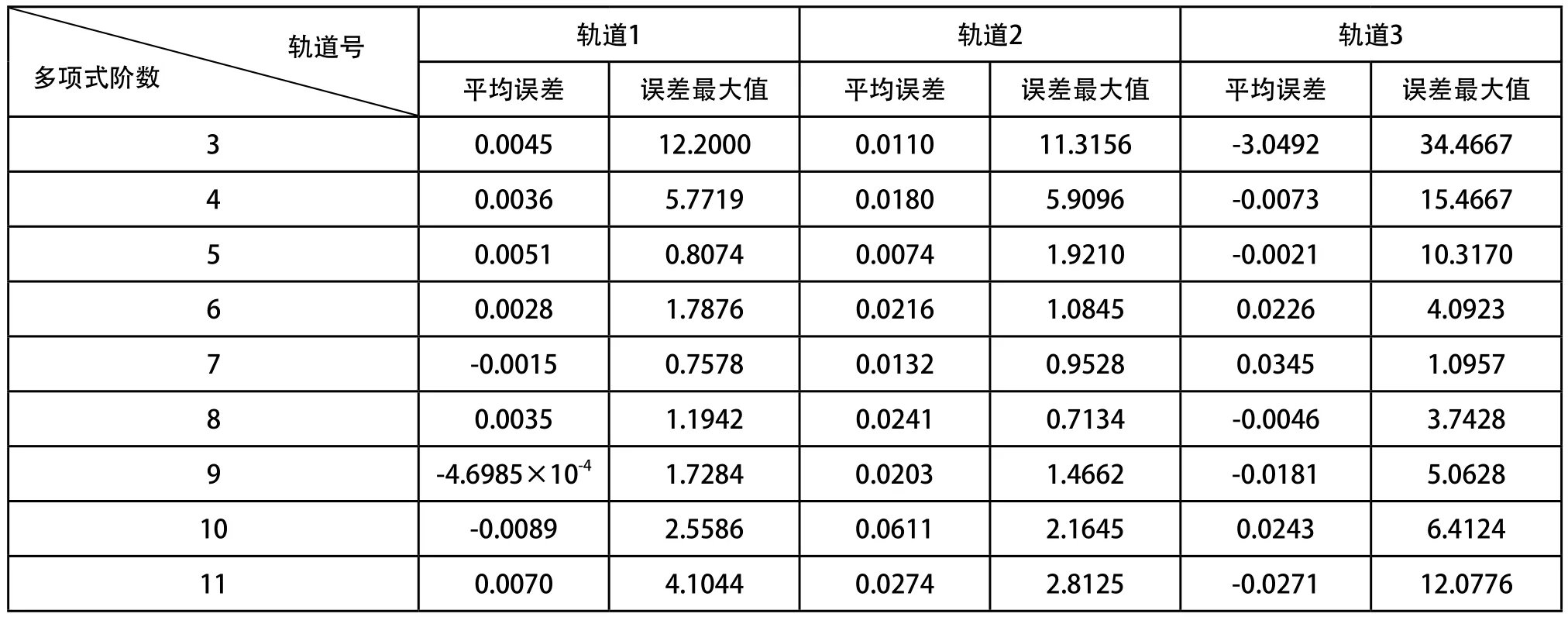
表1 三轨轨道数据的方位内插结果

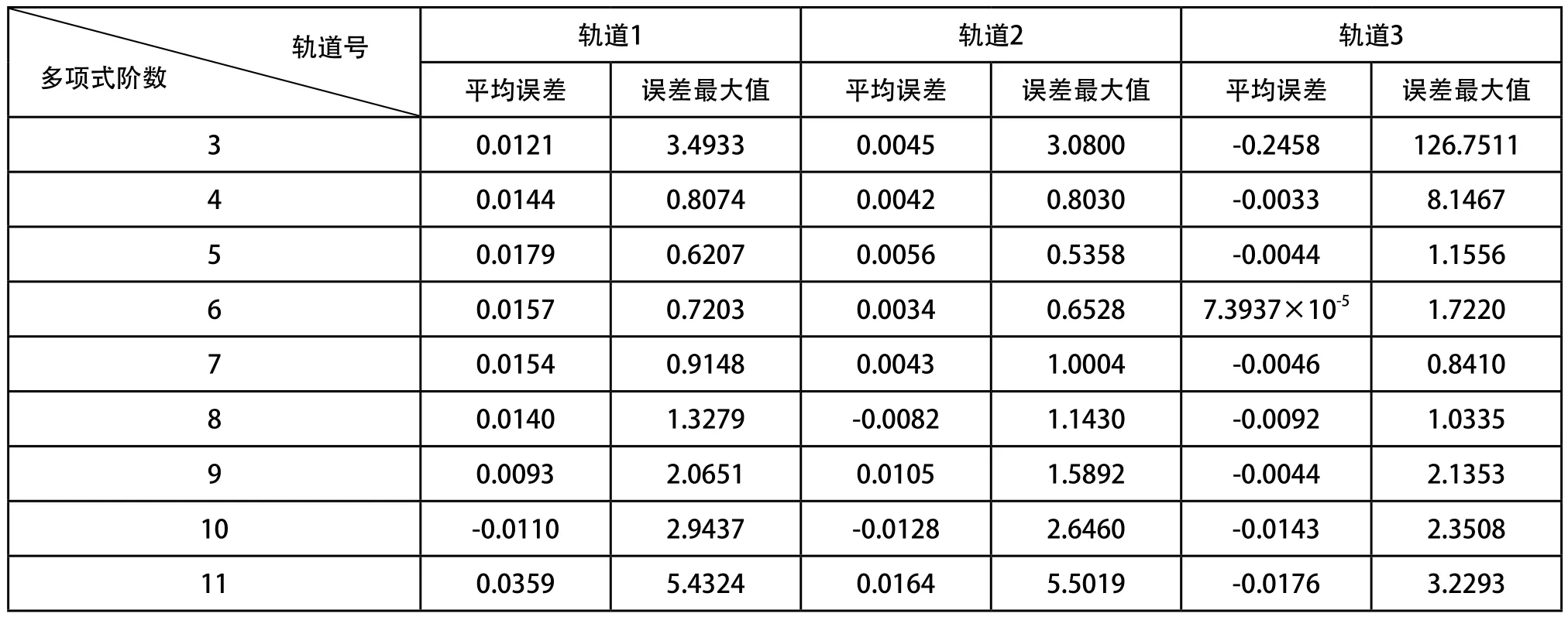
表2 三轨轨道数据的俯仰内插结果

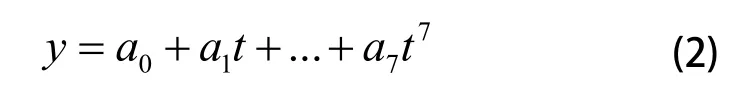
3 基于前馈补偿的增量式PID控制算法

3.1 增量式PID算法

增量式PID算法公式为：

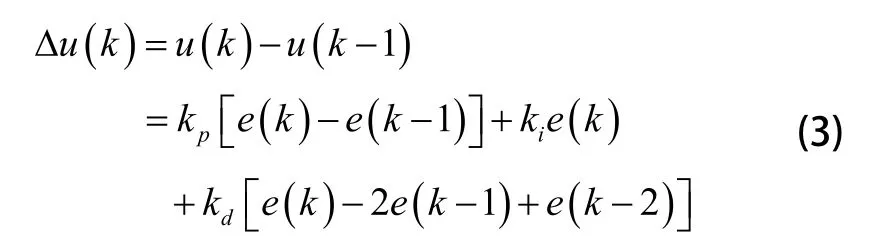
式中e(k-2)、e(k-1)和e(k)分别为(k-2)、(k-1)和k时刻所得的偏差信号。可以看出，参数kp、ki、kd一旦确定，只需使用前后3次测量值的偏差，则可根据式(3)计算控制量的增量。增量式PID控制望远镜跟踪卫星的原理框图如图4所示。

设定值r(t)为t时刻的卫星位置坐标（方位starAZt，俯仰starDECt），根据式(2)计算获得。读取此时望远镜两轴编码器读数头读数，方位currAZt，俯仰currDECt作为反馈值c(t)，负反馈给位置环中增量式PID控制器，得到该时刻的位置误差为：

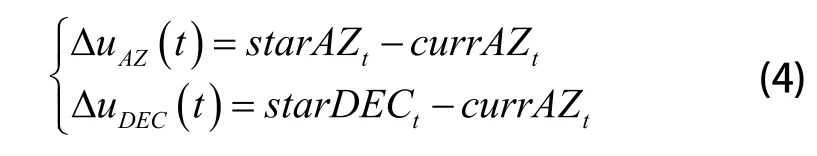
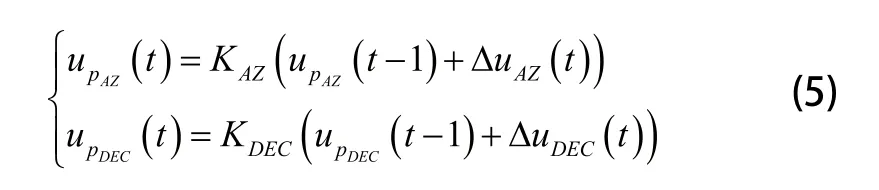
式中KAZ，KDEC均为常量，分别表示方位轴俯仰轴速度与电压的当量，值分别由各轴驱动器中设定的参数决定。分别为方位、俯仰轴当前t时刻增量式PID控制器的输出，为上一时刻即t-1时刻的控制器输出，分别根据方位前后3次测量的误差、俯仰前后3次测量的误差按照式(5)计算得到。PID控制器的输出作为驱动器速度环的给定，控制望远镜两轴速度。

3.2 前馈控制

前馈控制系统是根据扰动或给定值的变化按补偿原理来工作的控制系统，其特点是当扰动产生后，被控变量还未变化以前，根据扰动作用的大小进行控制，以补偿扰动作用对被控变量的影响[10]。在本系统中，前馈控制作为辅助控制加入到位置闭环控制中，控制原理图如图5所示。

在本系统中，设计前馈控制器的输出uf(t)与输入r(t)的关系表达式为：

式中r(t)表示t时刻的卫星位置坐标。根据式(2)、式(6)变为：

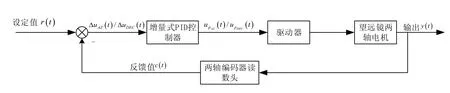
图4 增量式PID控制原理框图

图5 加入前馈补偿的增量式PID控制原理框图

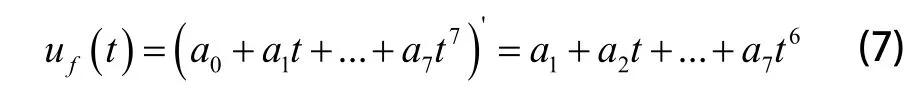
驱动器速度环的输入变为增量式PID控制器的输出加上前馈控制器的输出uf(t)。

4 实验结果

实验中，以图6所示的某卫星轨道文件作为望远镜的跟踪引导文件，分别采用加入前馈补偿和不加前馈补偿的PID控制算法在1m人卫激光测距望远镜中进行卫星轨道跟踪。两种控制算法下得到的望远镜两轴跟踪误差曲线分别为图7、图8所示。

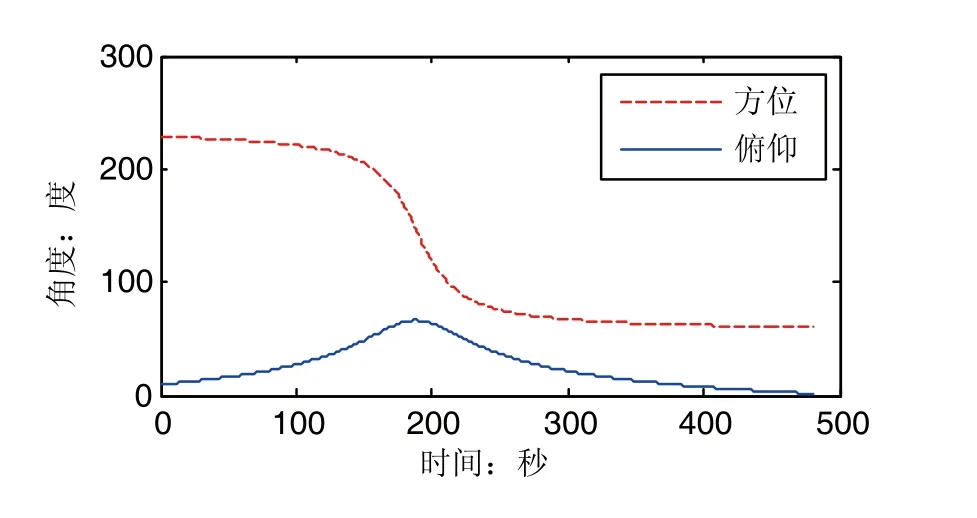
图6 卫星轨道引导值曲线图

图7 前馈补偿的PID控制算法下望远镜两轴的轨道跟踪误差曲线图

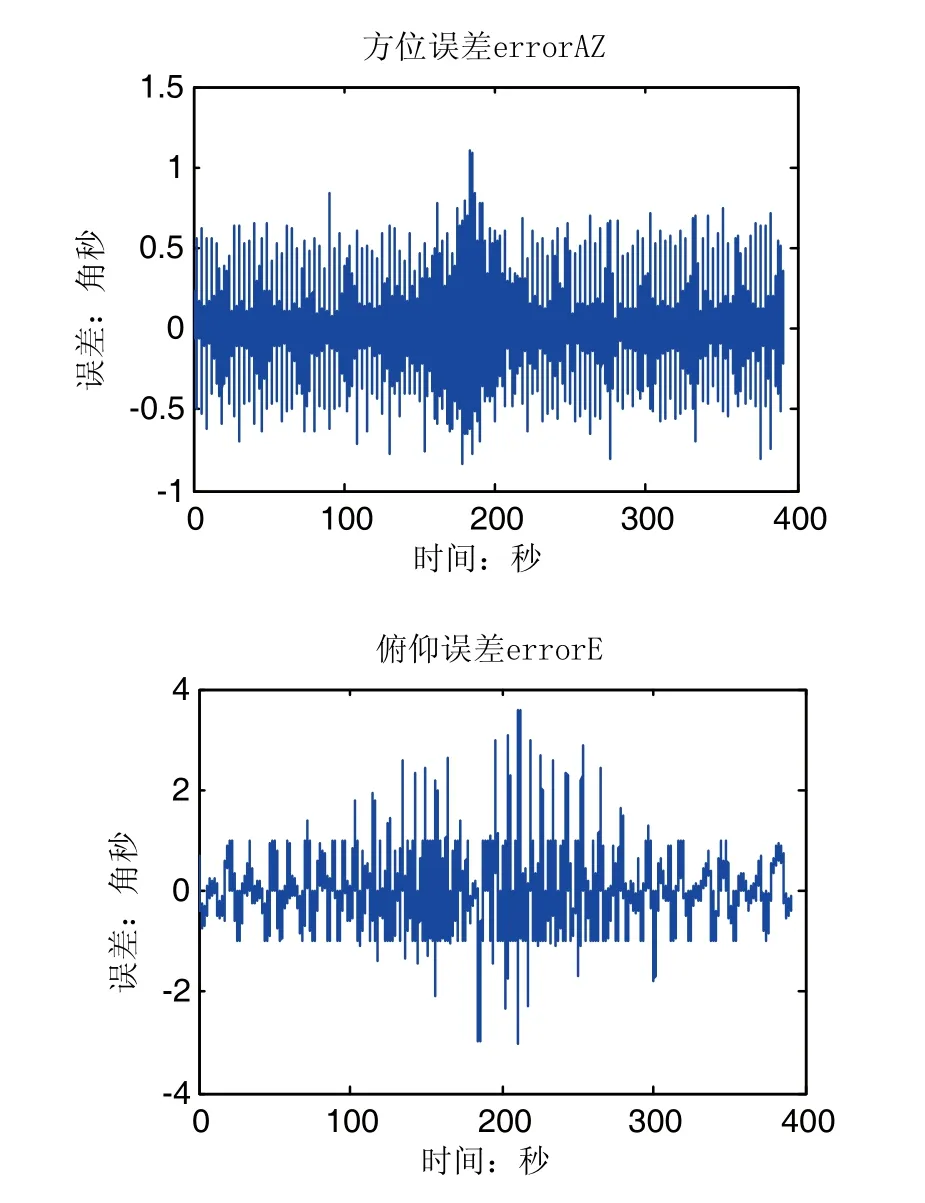
图8 不加入前馈控制的PID控制算法下望远镜两轴的轨道跟踪误差曲线图

在不加入前馈控制的情况下，望远镜方位轴跟踪误差均值1.1817，均方差1.3431，跟踪过程中最大误差可达15角秒；俯仰轴跟踪误差均值1.4682，均方差2.0502，跟踪过程中最大误差可达8角秒。加入前馈控制后，方位跟踪误差均值0.0015，均方差0.1254，跟踪过程中最大误差1角秒；俯仰轴跟踪误差均值-0.0009，均方差0.6863，跟踪过程中最大误差3.81角秒。

在不加入前馈控制的情况下，位置环只采用增量式PID控制，在低轨卫星速度变化迅速的阶段，望远镜的跟踪误差会变大，而加入前馈控制后，望远镜能很好的响应卫星速度的变化，响应更快，且跟踪精度更高，鲁棒性好，跟踪误差在1角秒以内。

5 结论

在人卫激光测距望远镜中，控制望远镜准确跟踪卫星是一个很重要的方面。望远镜稳定的、高精度的跟踪是保证回波信号能被接收的前提。本文介绍了一种前馈补偿的增量式PID算法与多项式内插算法相结合的卫星轨道跟踪方法。经实验表明，基于前馈补偿的增量式PID可以很好的应用于望远镜控制系统中，能准确地跟踪卫星，且导行精度优于2''，达到项目的预期目标。

[1]刘博婷.大口径望远镜主镜位置检测与控制[D].中国科学院研究生院(长春光学精密机械与物理研究所),2015.

[2]朱晓猛.位置PID控制在望远镜控制系统中的应用[J].微计算机信息,2011,(02)：78-79.

[3]吴春晖,朱庆生,周小军.全日面太阳光学和磁场望远镜的自动跟踪与导行方法[J].天文研究与技术,2007,(02)：147-152,146.

[4]王建峰,陈丽娜. 兴隆基地技术文档——星历预报软件PreTLE V3.0_for ali使用说明[Z].国家天文台,2016.

[5]何玉晶,杨力.基于拉格朗日插值方法的GPSIGS精密星历插值分析[J].测绘工程,2011,(05)：60-62.

[6]马俊,等.基于IGS精密星历的卫星坐标插值方法比较[J].城市勘测,2011,5：89-93.

[7]王世儒,等.计算方法[M].西安：西安电子科技大学出版社,1996.

[8]王青平,等.高采样率下GPS卫星轨道坐标插值方法比较[J].大地测量与地球动力学,2013,(05)：49-52.

[9]宫厚诚,李全海.基于IGS精密星历的卫星坐标和钟差插值[J].全球定位系统,2009,(05)：24-26,38.

[10]刘美,禹柳飞,宁鹏.仪表及自动控制[M].中国石化出版社,2015.10,222-224.