锂电池电化学传递函数模型的建立和验证

路金玲，张 希，靳 伟，周 轩

(1.上海交通大学机械与动力工程学院，上海200240；2.凯特林大学电气与计算机工程系，密歇根 弗林特48504)

锂电池技术是连接汽车与电网的关键核心技术之一，已应用于插电式混合动力汽车(PHEV)、混合动力汽车(HEV)、纯电动汽车(EV)中。在电池建模方面已经有了大量的研究，文献[1-5]中采用等效电路模型(ECM)，它不考虑电池内部的化学成分及反应，根据电特性，用电阻、电容、外部电压源等构成电路，这种方法模型简单，参数容易获得，但对模型参数不具有实际意义，估测不准确；文献[6-12]中采用电化学模型，是基于电化学机理用数学模型描述电池内部成分及反应变化情况，通过模型方程的简化获得数学模型，此方法精度高，但参数辨识过程复杂。本文将两种方法结合起来，由基于电化学机理获得的偏微分方程，通过数学推导得到与传递函数类似的表达式，以获得对电池荷电状态(SOC)和终端电压监测精度更高的模型，并通过Matlab建模，与Comsol仿真模型进行对比验证。

1 基本模型

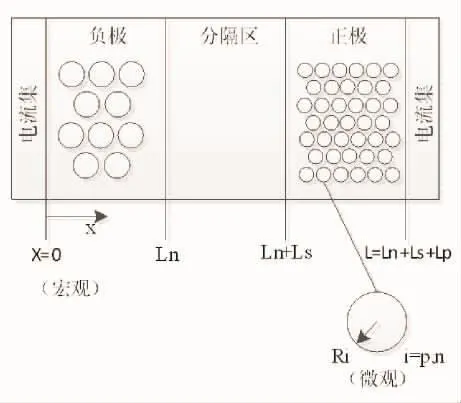
图1 锂离子电池结构

锂电池的结构如图1所示，正负电极处活性物质被氧化或还原，锂离子从电极中脱嵌或嵌入，并通过电解液进行传递。电极端部的活性物质被固定于电流集，由隔膜完成电隔离。假设电极内活性物质的性质只沿x轴方向改变，具体关系介绍如下。

电极和电解液接触的界面对电子的转移有抑制作用，这种作用产生了过电压，定义如下：

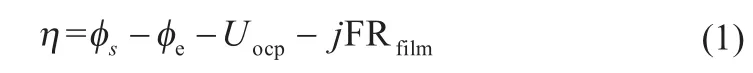
式中：φs、φe分别为固相电极、电解液电势；Uocp为开路电压；Rfilm为隔膜电阻。

由Butler-Volmer公式可得电池电流密度：

固相电极的浓度与电势关系[13]表达为：

液相电解质的浓度与电势关系[13]表达为：

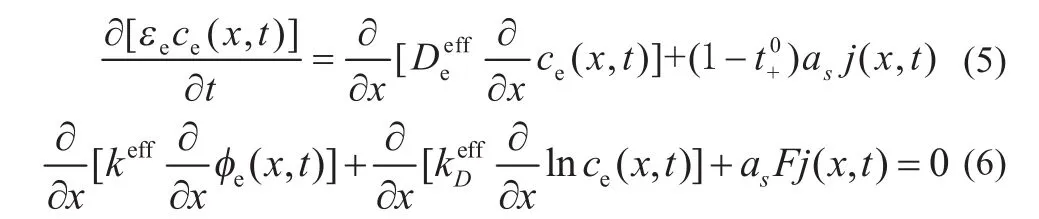
锂离子电池的微观粒子变化如上述公式所示，即我们所知的伪二维模型。基于此模型，经过一定的数学处理，可以对电池的性能进行估测。

2 传递函数模型

本文主要目的是获得电池电压的表达式。以伪二维模型为基础，电池的端电压可由公式(7)表示，各部分表达式计算方法如下：

2.1 开路电压

将式(3)进行拉普拉斯变换和变量代换，得到固相电极浓度与电流密度的关系：

将水平坐标x进行处理变为无量纲参数，则在正极处，变量化为变化范围为[0,1]；同理在负极处，变量化为变化范围为[0,1]。

将式(4)、式(6)相减，式(2)变形运算得到交换电流密度和输入电流的关系，由此可得固相电极离子浓度与输入电流间的关系，根据SOC的定义可得：

开路电压值Up(SOC)、Un(SOC)可通过查表获得。

2.2 过电压

将式(2)进行拉普拉斯变换，计算得到电极过电势：

正负极的过电势只需把相应的系数代入计算即可。

2.3 电解液电势差

计算电池电压时只需得到正负极终端的电势差，由式(6)可知，电解液电势差由两部分组成，第一部分在已知电解液浓度的基础上求解，表示如下：

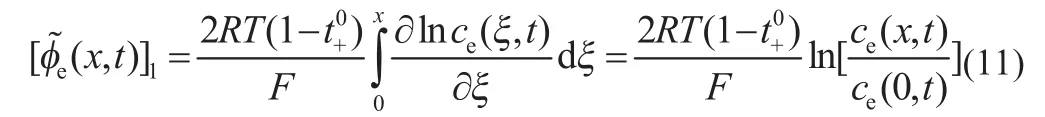
电解液浓度表达式如式(5)，由于正负极及分隔部分参数值不同可将其分为三部分，每部分均为常微分方程表达式。在边界条件和初始条件下联立方程组求解，可得电解液浓度和电流的关系式。

第二部分则根据位置不同，由不同电化学参数分段表示。

2.4 内阻压降

已知电池的内阻为Rf，对应的内阻压降为：

3 仿真验证

由上述表达式，在Matlab/Simulink环境下建模进行模型验证。

以Comsol4.3a模型库中的一维锂离子电池为比较对象，调整后通过Comsol with Matlab接口导入Matlab中，将Matlab/Simulink中的仿真结果通过To workspace模块导入工作空间中，不同工况下的电池仿真对比结果如图2所示。

图2 不同工况下的仿真结果

4 结论与展望

综上所述，基于电化学机理的传递函数模型可以在一定程度上反映电池端电压及内部电化学反应带来的实时变化。通过仿真结果的对比，此传递函数模型的估算误差在允许范围内。但由于电化学参数的数量众多，且参数随时间等外界因素有相应的变化，降低了模型的精度，在后续的研究中将通过dSPACE进行硬件在环实验，对电化学参数进行实时辨识，改进传递函数模型。

[1]李思.电动汽车锂离子电池等效电路模型的参数辨识研究[D].北京:北京理工大学,2015.

[2]LIAW B Y,NAGASUBRAMANIAN G,JUNGST R G,et al.Modeling of lithium ion cells-a simple equivalent-circuit model approach[J].J Power Sources,2004,175(1/4):835-839.

[3]HU Y,YURKOVICH S,GUEZENNEC Y,et al.Electrothermal battery model identification for automotive applications[J].J Power Sources,2011,196(1):449-457.

[4]HU Y,YURKOVICH S.Linear parameter varying battery model identification using subspace methods[J].J Power Sources,2011,196(5):2913-2923.

[5]HU X S,LI S B,PENG H.A comparative study of equivalent circuit models for Li-ion batteries[J].J Power Sources,2012,198:359-367.

[6]GUO M,SIKHA G,WHITE R E.Single-particle model for a lithiumion cell:thermal behavior[J].J Electrochem Soc,2011,158(2):A122-A132.

[7]RAHIMIAN S K,RAYMAN S,WHITE R E.Extension of physicsbased single particle model for higher charge-discharge rates[J].J Power Sources,2013,224:180-194.

[8]LUO W L,LYU C,WANG L X,et al.A new extension of physicsbased single particle model for higher charge-discharge rates[J].J Power Sources,2013,241:295-310.

[9]RAHIMIAN S K,RAYMAN S,WHITE R E,et al.Comparison of single particle and equivalent circuit analog models for a lithium-ion cell[J].J Power Sources,2011,196:8450-8462.

[10]SMITH K A.,RAHN C D,WANG C Y.Control oriented 1D electrochemical model of lithium ion battery[J].J Power Sources,2007,48(9):2565-2578.

[11]GAMBHIRE P,GANESAN N,BASU S,et al.A reduced order electrochemical thermal model for lithium ion cells[J].J Power Sources,2015,290:87-101.

[12]FORMAN J C,BASHASH S,STEIN J L,et al.Reduction of an electrochemistry-based Li-ion battery model via quasi-linearization and Padé approximation[J].J Electrochem Soc,2011,158(2):A93-A101.

[13]RAHN C D,WANG C Y.Battery systems engineering[M].US:Wiley,2013.