定向凝固Fe-Mn-C-Al系TWIP钢枝晶生长行为的研究

丁 浩 刘建华 闫柏军 刘洪波 申耀祖

(1.北京科技大学工程技术研究院； 2.北京科技大学冶金与生态工程学院)

0 前言

TWIP钢兼具高的强度、塑性和应变硬化性能，被认为是理想的新一代汽车用钢，对汽车轻量化的实行，有效地实现节能减排，降低大气污染，有非常大的发展前景[1]。笔者使用定向凝固技术，并结合光学显微镜对Fe-Mn-C-Al系TWIP钢的枝晶生长行为进行了研究，对于TWIP钢的基础研究具有重要意义。

1 实验方法

1.1 实验材料和设备

将工业纯铁、锰、铝和碳作为原料，在真空感应炉中熔炼并使用铸铁模进行真空浇注，得到25 kg Fe-Mn-C-Al TWIP钢铸锭，切除冒口。铸锭形状尺寸和取样位置如图1所示。在S1和S2位置取钻屑，以这两个位置的平均成分作为铸锭的成分。在图示位置取6根Φ6×100 mm的棒状试样用于定向凝固试验，定向凝固样品的取样位置都靠近铸锭外表面，故而钻屑S1和S2的成分与定向凝固试样的成分之间应该不存在明显差别。钻屑的成分分析结果见表1。

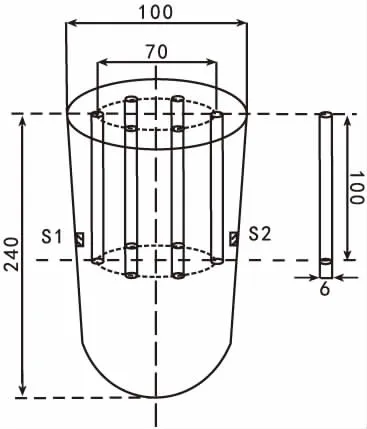
图1 样品尺寸和取样位置

元素FeMnCAl含量,%余量18.020.681.35

本研究采用DJL-500 Bridgeman定向晶体生长炉，分别以25 μm/s、50 μm/s和100 μm/s的抽拉速率进行定向凝固实验，凝固界面前沿的温度梯度(G)约为10 K/mm。

1.2 样品处理

线切割获得定向凝固试样的纵向截面，经过打磨、抛光后，对纵向截面进行化学侵蚀并使用光学显微镜观察其凝固组织。利用公式计算不同抽拉速率下的一次、二次枝晶间距，其中L为实测长度，n为实测长度内一次或二次枝晶个数，对于同一凝固速率，应选取不同的区域多次测量后取其平均值。

2 实验结果及讨论

2.1 液固界面形貌

受到合金系统内在和外界条件外在的影响，液固相变中凝固界面具有多种形态。液固界面在移动速度不断增加的过程中，其形态由接近平衡状态的平界面逐步发展为胞状、胞枝状及完整的树枝状界面，再由树枝状转变为远平衡态的胞状界面，进而转变为针、带状界面，最终达到更高层次的平界面。本Fe-Mn-C-Al系TWIP钢具有较宽的结晶温度间隔，在10 K/mm的温度梯度下，其在较小的抽拉速度下就会发生界面失稳而形成枝晶结构。

在25 μm/s～100 μm/s的抽拉速度范围内，Fe-Mn-C-Al系TWIP钢定向凝固界面形态的演化如图2所示。

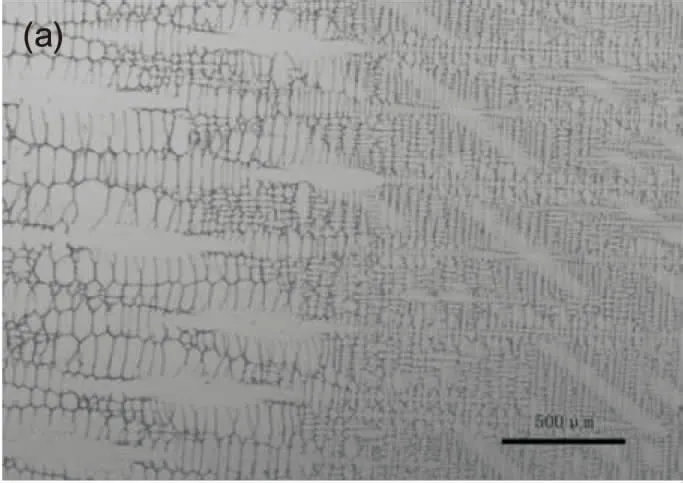
(a) 25 μm/s界面处组织形貌

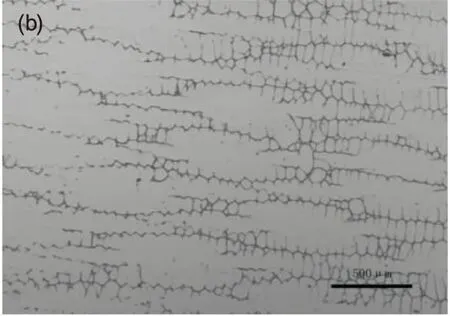
(b) 25 μm/s固相组织形貌

(c) 50 μm/s界面处组织形貌

(d) 50 μm/s固相组织形貌

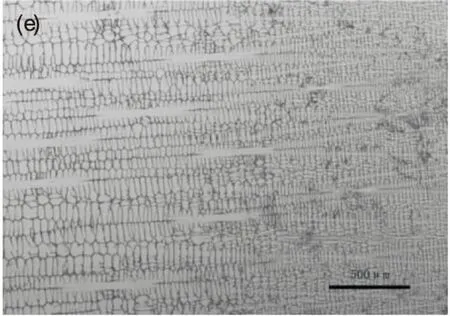
(e) 100 μm/s界面处组织形貌

(f) 100 μm/s固相组织形貌

从图2可以看出，在本实验抽拉速度范围内，界面形态随着抽拉速度的增加，逐渐由比较粗大的树枝晶转变为细小枝晶，没有胞枝晶转变的现象。抽拉速度为25 μm/s时，凝固界面呈现典型的枝晶形态，具有较为发达的二次枝晶。在定向凝固试验中，凝固冷却速度决定了液固界面内的散热能力。冷却速率的增大使得液固界面内具有更强的散热能力。这样，在较大的凝固冷却速度时，通常会出现更小的枝晶排列。

在抽拉速率由25 μm/s增加到100 μm/s的过程中，枝晶组织逐渐细化，一、二次枝晶间距都有较为显著的减小，当抽拉速率为100 μm/s时，一次枝晶间距减小到119.9 μm，二次枝晶间距减小到47.4 μm，具体测试数据见表2。

表2 TWIP钢一次枝晶间距λ1、二次枝晶间距λ2的测试结果

2.2 枝晶间距

Hunt[2]首先建立了一次枝晶间距的预测模型，该理论模型考虑了一些凝固参数的作用，其表达式为：

(1)

式中：G——液固界面前沿的温度梯度，K/m；

V——凝固速度，m/s；

D——溶质元素在液相中的扩散速率，m2/s；

Г——溶质元素的Gibbs-Thompson系数，m·K；

m——液相线斜率；

k——溶质元素的平衡分配系数；

C0——溶质元素初始的浓度。

当晶体的生长形式为树枝晶时，式(1)变成：

(2)

Kurz-Fisher[3]模型假设枝晶形貌为椭球形，在枝晶生长速度较高时，该模型对于一次枝晶臂间距的预测为:

(3)

式中：△T0——固液相线温度差，△T0=mC0(k-1)/k，K。

Trivedi[4]模型则考虑了简谐扰动的影响，其一次枝晶臂间距的预测为：

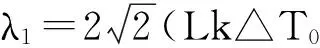
(4)

式中：L——简谐扰动常数，L=(l+1)(l+2)/2，晶体生长形式为枝晶时，l=6，则L为28。

Masana Imagumbai[5]研究了一次枝晶臂间距与二次枝晶臂间距的关系，在实验的基础上提出了二次枝晶间距的表达式为：

(5)

式中：R——m/s；

tf——局部凝固时间，s，tf=△T0/RG。

p取1/3，则式(5)可以化简为：

λ2=6.8(DГ/RGk)1/3

(6)

Furer和Wunderlin[6]假设较小的二次枝晶臂进行侧向重熔，从而使得二次枝晶臂间距增加：

λ2=5.5(Atf)1/3

(7)

Cl——液相溶质元素的浓度；

ml——液相线斜率。

Edvardsson等人[7]比较了若干具有不同碳含量的锰钢，发现二次枝晶臂间距可用λ2=K(G,R)n形式的表达式来计算，根据本实验条件，其关系式可确定为：

λ2=110×Rc-0.173

(8)

式中：λ2——二次枝晶间距，μm；

RC——钢水冷却速率，K·min-1。

使用专业热力学软件Thermo-calc对本实验用TWIP钢进行计算，得到kMn=0.76。

液相线温度采用公式：

TL=1537-55.3(%C)-18.7(%Si)+(-3.76-0.86%C)(%Mn)+0(%Al)

(9)

固相线温度采用公式:

(10)

其中，

Ce=(80.5[C]+33.5[S]+33.5[P]+3.75[Mn]+17.8[Si]+3.4[Co]+3.8[Al]+1.5[Cr]+3[Ni])/80.5

(11)

计算得△T0=TL-TS=178.4K。

将相关参数D=2.4×10-9m2·s-1，Г=1.0×10-7K·m分别代入式(2)、式(3)、式(4)中，得到表3的表达式。

表3 本实验TWIP钢三种一次枝晶间距理论模型的数学表达式

通常来说，一次枝晶间距与生长速率和温度梯度之间存在一个二元指数关系，即λ1满足与R和G的指数关系：

λ1=CR-mG-n

(12)

其中，m、n为常数，受合金性质、温度梯度和生长速度等因素影响。C也为常数，随着关系式的不同而不同，不同学者提出的关于λ1的预测表达式不同，C也不同。由表3可以看出，在已知实验中各项参数时，一次枝晶臂间距预测表达式具有相似的形式，其中指数m都为1/4。

同理，将相关参数代入式(6)、式(7)和式(8)中，得到表4。

表4 本实验TWIP钢三种二次枝晶间距理论模型的数学表达式

对于二次枝晶间距来说，不同学者对于其粗化过程的假设不同，一般将二次枝晶臂间距λ2表述为与局部凝固时间tf或冷却速率CR之间的关系：

λ2=A·tfm或λ2=B·CR-n

(13)

式中，A、B为系数，受合金成分影响；CR=G·R，指数m、n为常数，数值大小与不同学者提出的假设有关。从表4化简得出的三种表达式可以看出，其也都具有相似的形式。

实验值与不同理论预测模型的计算值之间的关系如图3、图4所示。

图3 一次枝晶臂间距随凝固速率的变化

图4 二次枝晶臂间距随凝固速率的变化

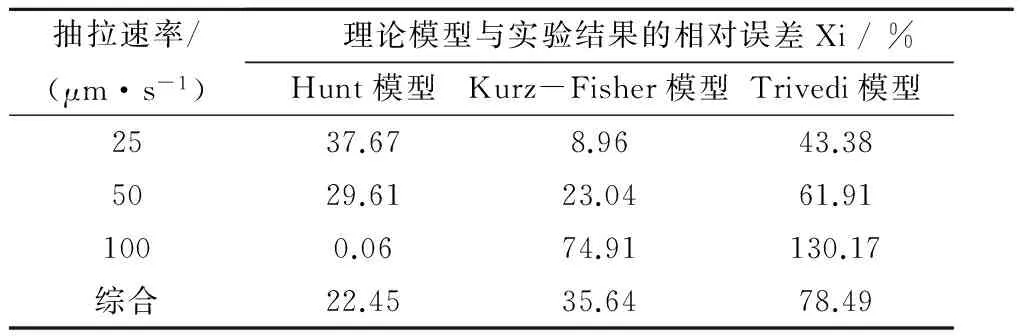
表5 一次枝晶臂间距理论模型与实验结果误差比较

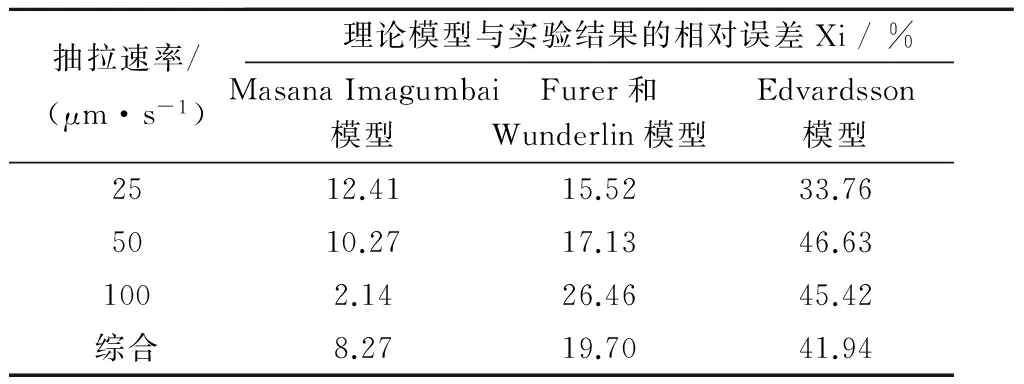
表6 二次枝晶臂间距理论模型与实验结果误差比较

计算得出Hunt、Kurz-Fisher、Trivedi三种一次枝晶臂间距模型的综合误差率分别为22.45%、35.64%、78.49%；Masana Imagumbai、Furer和Wunderlin、Edvardsson三种二次枝晶臂间距模型的综合误差率分别为8.27%、19.70%、41.94%。对于一次枝晶臂间距，其实验结果分布于Hunt模型和Kurz-Fisher模型范围之间。在凝固速率较低(25 μm/s)时，实验结果与Kurz-Fisher模型匹配效果较好，而随着凝固速率的增加，当凝固速率比较大(100 μm/s)时，实验结果与Hunt模型吻合较好，预测结果更加准确。对于二次枝晶臂间距，其实验结果分布于Furer和Wunderlin模型及Masana Imagumbai模型之间，且在凝固速率为25 μm/s～50 μm/s范围内，二者预测结果误差相当，而在凝固速率增加(100 μm/s)时，Masana Imagumbai模型与实验结果相吻合。整体看来，经典的一次枝晶间距预测模型中只有Hunt模型的预测效果相对较好一些，而Masana Imagumbai模型对于本文TWIP钢二次枝晶间距预测效果非常理想。

Hunt模型与Kurz-Fisher模型都将合金体系的成分及合金凝固区间作为考虑因素，两者不同的是Hunt模型将一次枝晶形状假设为胞状面，而Kurz-Fisher模型则将其假设为轴对称椭圆面，考虑可能正是由于这些假设的差异，较大程度地影响了两种模型对本实验的预测效果。

Masana Imagumbai模型是在理论基础上结合具体实验所得，其实验所用钢的成分分别为：钢种a，0.62%C-0.12%Si-0.58%Mn-0.006%P-0.073%S-0.049%Al-0.001 1%O；钢种b，0.52%C-0.10%Si-0.56%Mn-0.003%P～0.046%S-0.037%Al-0.001 1%O。而本钢种的Mn元素含量明显高于Masana Imagumbai模型中实验用钢的Mn元素含量，这可能会是其预测结果出现误差的原因。总体来说，Masana Imagumbai模型对于本钢种二次枝晶臂间距预测的综合误差率仅为8.27%，效果非常好。

3 结论

(1)在实验条件抽拉速率范围内，Fe-Mn-C-Al系TWIP钢的凝固组织均为枝晶组织，并未出现胞晶组织，且随着抽拉速度的增加枝晶被明显细化，一次枝晶间距、二次枝晶间距不断减小。

(2)Hunt、Kurz-Fisher、Trivedi三种一次枝晶臂间距模型的综合误差率分别为22.45%、35.64%、78.49%，在25 μm/s～50 μm/s的凝固速率范围内，Kurz-Fisher模型的预测结果较为准确，在凝固速率较大(50 μm/s)时，Hunt模型的预测与实验结果吻合较好。

(3)Masana Imagumbai、Furer和Wunderlin、Edvardsson三种二次枝晶臂间距模型的综合误差率分别为8.27%、19.70%、41.94%，在整个实验凝固速率范围内，Masana Imagumbai模型对于本Fe-Mn-C-Al系TWIP钢定向凝固实验 结果预测效果较好。

[1] Liu H B, L J H, Michelic S, et al. Characterization and Analysis of Non-Metallic Inclusions in Low-Carbon Fe-Mn-Si-Al TWIP Steels[J]. Steel Research International, 2016, 87(12): 1723-1732.

[2] Hunt J D. Solidification and Casting of Metals[M]. London: The Metal Society, 1979：3-12.

[3] Kurz W, Fisher D J. Dendrite growth at the limit of stability: tip radius and spacing[J]. ActaMetallurgica, 1981, 29(1): 11-20.

[4] Trivedi R. InterdendriticSpacing: Part II. A Comparison of Theory andExperiment[J]. Metallurgical Transactions A, 1984, 15A: 977-982.

[5] Imagumbai M. Relationship between Primary-and Secondary-dendrite Arm Spacing of C-Mn Steel Uni-directionally Solidified in Steady State[J]. ISIJ International, 1994, 34(12): 986-991.

[6] Salas G B, Ramírez J V, Noguez M E A, et al. Dendrite arm spacing—Local solidification time relationship: An experimental model for a 70-30 brass and its comparison with some theoretical models[J]. Scripta metallurgica et materialia, 1995, 32(2): 295-299.

[7] EdvardssonT,Fredriksson H,Svensson I, et al. A study of the solidification process in low-carbon manganese steels[J]. Metal Science,1976,10(9):298-306.