多关节机器人的自适应阻抗控制研究

孙 晓，杨守平，王 兴，夏运贵，刘 方

（1.湖南工业大学 机械工程学院，湖南 株洲 412007；2.湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

1 研究背景

动车组侧窗玻璃除了防止冲击，还要保证其密封性能与视觉效果，其材质和安装都非常重要。目前侧窗安装主要由人工完成，人工在作业时效率比较低、劳动强度也比较大。随着我国高铁事业的快速发展，对车辆的需求越来越大，人工安装动车组侧窗玻璃的效率问题越来越突出。采用带力回馈的机器人进行侧窗安装，依托与侧窗玻璃接触的力回馈信息，合理调整安装角度、密封压力和涂胶轨迹，可很好地解决这些矛盾，提高安装效率，进一步提高安装质量，对动车的组装具有较好的研究意义。阻抗控制作为其中的控制方法之一，在实现机器人在力和位置控制中得到了广泛的应用[1-6]。阻抗控制通过使机器人末端的力和位置达到一种理想关系，将力控制和位置控制纳于一个框架之内，实现较小的工作量[7-8]。当机器人和环境参数已知时，阻抗控制比较简单。但在实际应用中，由于机器人系统本身是一个非线性、强耦合、易受干扰的复杂系统，且存在各种不确定因素，机器人本身和环境模型的不精确或无法获取相关参数，导致阻抗控制存在很大的力误差[9]。

目前随着工业自动化程度的不断提高，对机器人末端力的控制精度要求也越来越高，因此国内外专家对机器人末端力的控制方法进行了大量研究。机器人末端力控制方法主要有阻抗控制[10]、混合力控制、力/位置控制等，其中阻抗控制因具有很强的适应性，适合在一些特殊环境下应用。文献[11]对二关节机器人进行了自适阻抗控制研究，但在实际运用中机器人都为多关节机器人，因此对多关节机器人的研究非常有必要。文献[12]采用神经网络对阻抗参数进行估计，使其对力的控制更加稳定，但对环境的要求较高，实际运用较难。文献[13]运用自适应的阻抗控制方法对幕墙安装机器人柔顺操作进行了研究，但只对机器人进行二关节控制。

本文研究了一种多关节机器人自适应的阻抗控制算法，通过建立动车组侧窗玻璃安装机器人接触阻抗控制模型，实现对机器人末端接触力的准确控制。图1为动车组侧窗玻璃安装机器人工作图。

图1 动车组侧窗玻璃安装机器人工作图Fig.1 A physical map of side window glass installation robots on EMU

2 数学模型

首先对机器人动力学模型进行介绍，然后对动车组侧窗玻璃安装和涂胶机器人接触建立阻抗控制模型。

2.1 机器人动力学模型

N自由度的机器人关节空间的动力学方程[11-12]如式（1）所示：

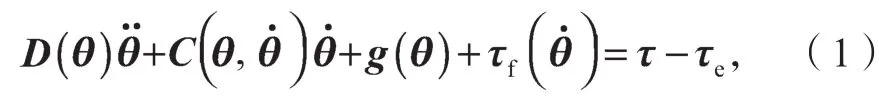
式中：θ为关节机器人各个关节的位移向量；为关节角速度向量；为关节加速度向量；D(θ)为机器人n×n惯性矩阵；为机器人n×1哥氏力矩及向心力矩向量；g(θ)为机器人各个连杆重力力矩；τ为机器人n×1关节驱动力矩；τf为n×1关节摩擦力矩；τe为n×1外部环境对机器人的作用力矩。

2.2 阻抗控制模型

动车组侧窗玻璃安装和涂胶机器人接触阻抗控制模型[13-14]如图2所示。其中：Fd为末端期望作用力；Fe为机器人末端与侧窗实际接触力；M为阻抗控制器的质量矩阵；B为阻抗控制器的阻尼矩阵；K为阻抗控制器的刚度矩阵。

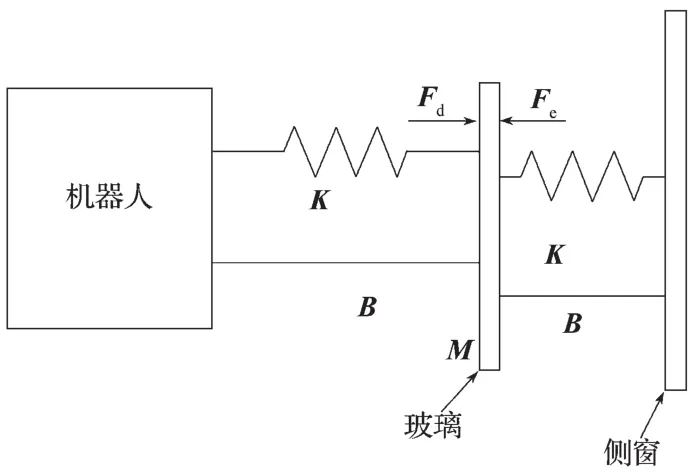
图2 机器人末端与侧窗接触阻抗控制模型Fig.2 A contact impedance control model of robot ends and side windows

3 自适应阻抗控制器的设计

根据自适应阻抗控制算法的控制思想，课题组在基础阻抗控制关系式中引入期望力，则阻抗控制关系式为

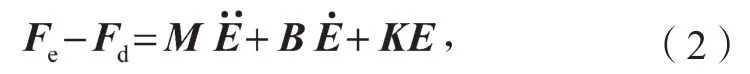
式中E为位置偏差。

由式（2）可知，当机器人与环境接触时，为达到稳定条件（Fe=Fd），设定力控制方向上K=0。

为了减少机器人力控制中存在的误差，在关系式中加入一个补偿项Ω来抵消产生的力误差，则式（2）可以改写为

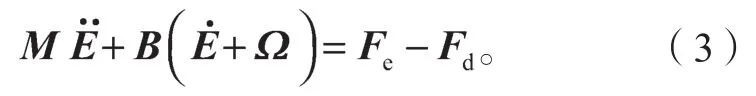
式中Ω为补偿项，其表达式为

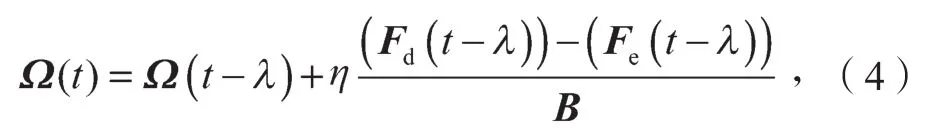
其中：t为时间；λ为控制器采样周期[11]；t-λ为t的前一周期；η为更新率。

由式（3）得

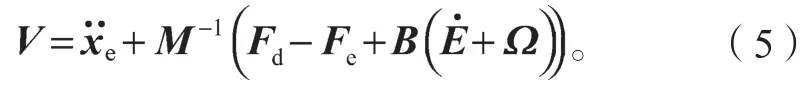
式中xe为机器人末端环境位置。

在实际控制中很难得到τ(t)、的值，因此使用前一周期的τ(t-λ)、(t-λ)代替当前的τ(t)、(t)。

在机器人动力学方程中引入控制器的采样时间，则机器人的动力学方程式（1）可以改写为

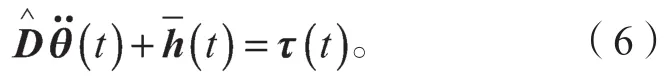
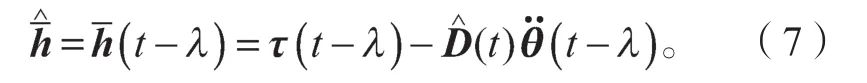
由式（6）（7）可知，机器人控制规律可写成

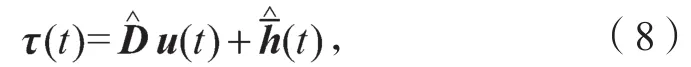
则自适应阻抗控制规律为

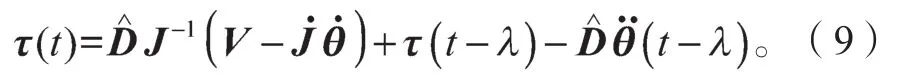
图3为机器人自适应阻抗控制系统结构框图。图中Xd为机器人仅在一个方向上受力时的末端位置。

图3 自适应阻抗控制系统结构框图Fig.3 A structure diagram of the adaptive impedance control system

4 仿真研究

为了验证本文所提控制策略的有效性，以PUMA560机器人前三关节被控对象进行仿真研究，其动力学方程如下：

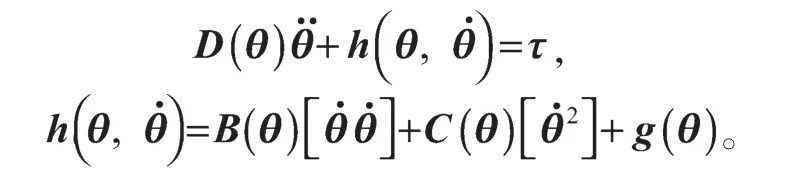
式中：B(θ)为n×n的哥氏力矩矩阵；C(θ)为n×n的向心力矩矩阵；

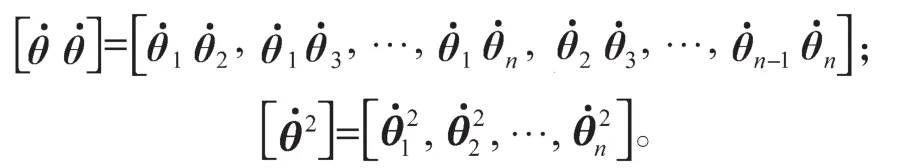
设机器人的末端为P(X,Y,Z)，机器人的第1个关节的起始关节角位置矢量角度为0，第2个关节的起始关节角位置矢量角度为-π/4，第3个关节的起始关节角位置矢量角度为5π/6，2个关节的速度均为0。末端的初始位置为P0(0.728 9,0.150 1,0.212 8)。对机器人末端加入期望的位置信号P1(0.738 9,0.150 1,0.202 8)，环境信号为P2(0.728 9,0.150 1,0.212 8)，阻抗控制的刚度矩阵如下：

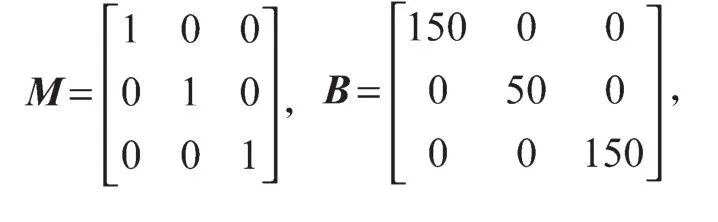
设期望力：FX=10 N，FY=0 N，FZ=10 N（FX、FY、FZ分别为X、Y、Z方向上机器人期望力）；X方向上的环境刚度KeX=4 000，Y方向上的环境刚度设为0，Z方向上的环境刚度KeZ=4 000。机器人初始位置示意图如图4所示。

图4 机器人初始位置示意图Fig.4 A schematic diagram of the robot’s initial position

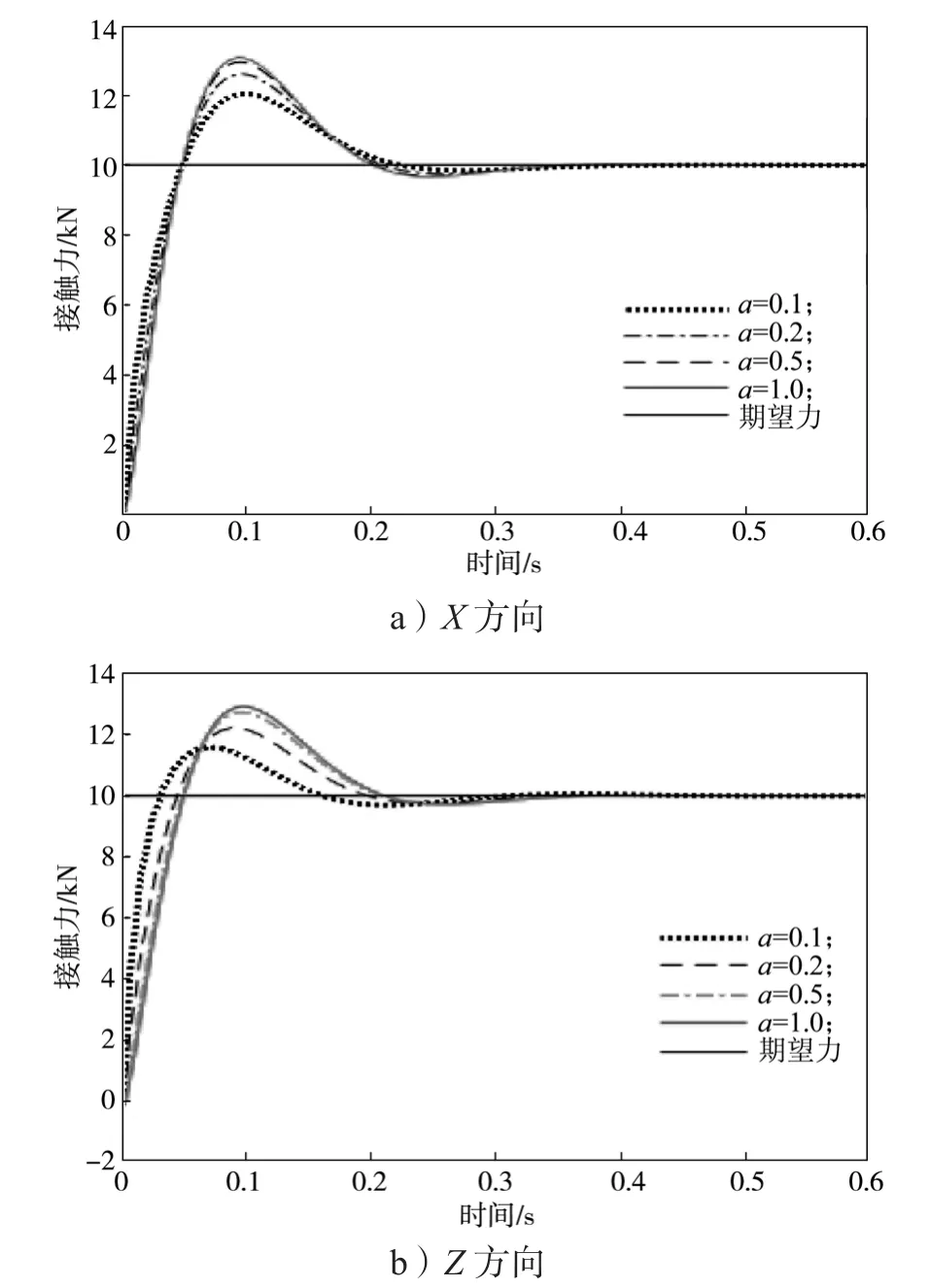
图5 惯性矩阵D对接触力的影响Fig.5 In fluence of the inertia matrix D on the contact force

由图5可以看出，在α=0.1时，力的曲线较为平滑，超调量最小，力的跟踪性能较好。当α=0.1时对机器人末端的位置跟踪情况如图6所示。

图6 机器人末端的位置跟踪情况Fig.6 Position tracking of the robot end

对机器人末端的接触力跟踪如图7所示。

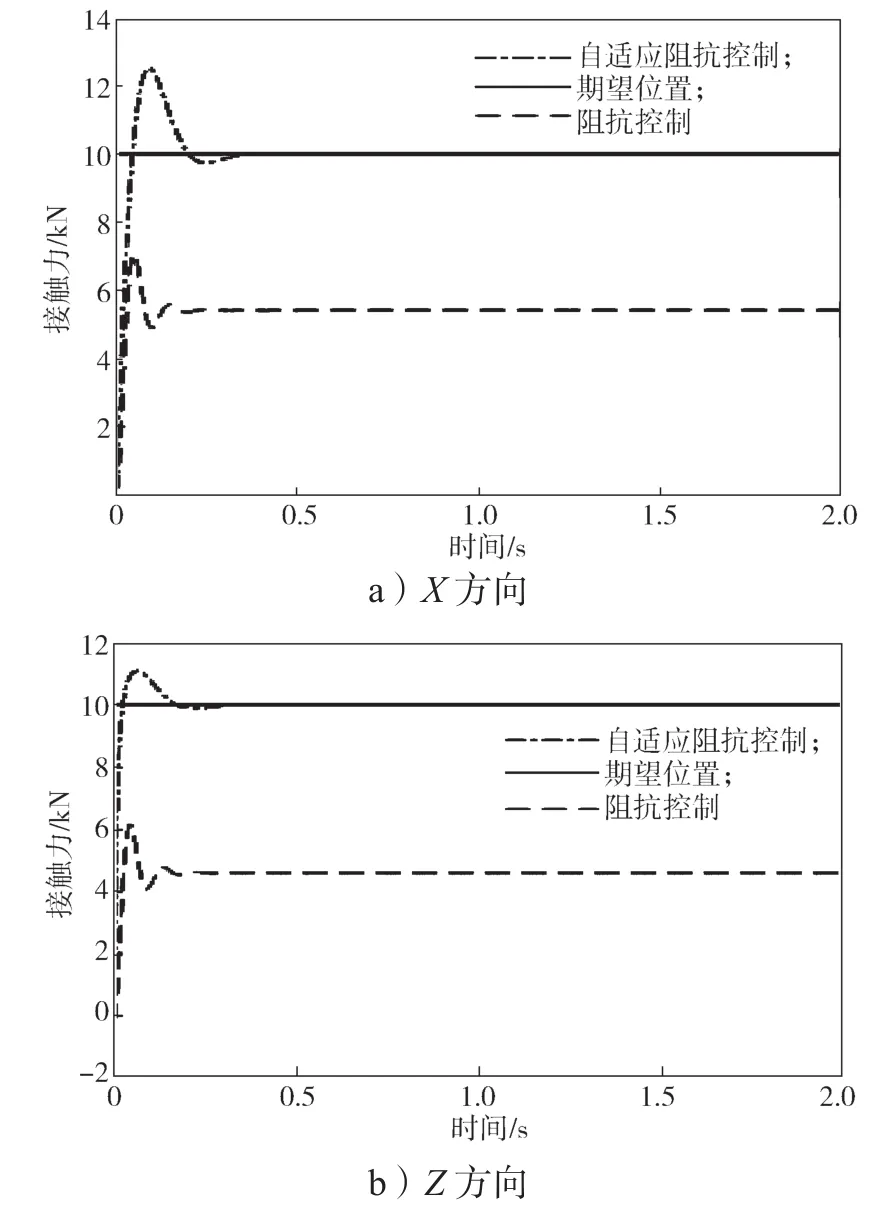
图7 机器人末端的接触力情况Fig.7 Contact force at the end of the robot

从图6可以看出，X方向期望位置为0.738 9，自适应阻抗控制跟踪位置为0.731 5，阻抗控制跟踪位置为0.730 5；Z方向期望位置为0.202 8，自适应阻抗控制跟踪位置为0.210 5，阻抗控制跟踪位置为0.211 8。两种控制在0.5 s后都达到稳定，自适应阻抗控制跟踪位置更接近期望位置。

从图7可以看出，X方向接触，自适应阻抗控制在0.5 s后跟踪上期望力10.0 N，阻抗控制力为5.4 N；Z方向接触，自适应阻抗控制在0.5 s后跟踪上期望力10.0 N，阻抗控制力为4.6 N。因此，自适应阻抗控制更能对机器人末端力进行精确控制。

5 结语

本文通过研究一种多关节机器人自适应阻抗控制策略，通过对PUMA560机器人前3个关节进行自适应阻抗控制研究，实现了对机器人末端力精确控制。仿真结果表明，自适应阻抗控制对自由空间的位置跟踪和接触空间的力跟踪都有很好的性能。本文的工作可为动车组侧窗玻璃安装机器人末端接触力控制应用研究提供借鉴。

[1]蔡自兴.机器人学[M].北京：清华大学出版社，2000：10-20.CAI Zixing.Robotics[M].Beijing：Tsinghua University Press，2000：10-20.

[2]霍 伟．机器人动力学与控制[M].北京：高等教育出版社，2005：51-110.HUO Wei.Robot Dynamics and Control[M].Beijing：Higher Education Press，2005：51-110.

[3]李 杰，韦 庆，常文森，等.基于阻抗控制的自适应力跟踪方法[J].机器人，1999，21(1)：23-29.LI Jie，WEI Qing，CHANG Wensen，et al.Adaptive Force Tracking in Impedance Control[J].Robot，1999，21(1)：23-29.

[4]SEUNG Y L.Glazed Panel Construction with Human Robot Cooperation[D].Daegu：Daegu Gyeongbuk Institute of Science and Technology，2011．

[5]CHEN I M，YANG G.Configuration Independent Kinematics for Modular Robots[C]//IEEE International Conference on Robotics and Automation.Minneapolis：IEEE，1996：1440-1445.

[6]SLOTINE J E，LI W P．应用非线性控制[M].北京：机械工业出版社，2009：30-40.SLOTINE J E，LI W P.Applied Nonlinear Control[M].Beijing：Machinery Industry Press，2009：30-40.

[7]崔 亮.机器人柔顺控制算法研究[D].哈尔滨：哈尔滨工程大学，2013.CUI Liang.The Research of Compliance Control Algorithms on Robot[D].Harbin：Harbin Engineering University，2013.

[8]刘 杰.上肢外骨骼式康复机器人控制系统研究[D].青岛：青岛大学，2012.LIU Jie.Research on Control System of Upper Limb Exoskeleton Rehabilitation Robot[D].Qingdao：Qingdao University，2012.

[9]符 浩.基于自适应神经网络的复杂机械臂控制研究[D].株洲：湖南工业大学，2016.FU Hao.Research on Complex Manipulator Control Based on Adaptive Neural Network[D].Zhuzhou：Hunan University of Technology，2016.

[10]李正义，曹汇敏.适应环境刚度、阻尼参数未知或变化的机器人阻抗控制方法[J].中国机械工程，2014，25(12)：1581-1585.LI Zhengyi，CAO Huimin.Robot Impedance Control Method Adapting to Unknown or Changing Environment Stiffness and Damping Parameters[J].China Mechanical Engineering，2014，25(12)：1581-1585.

[11]杨 振.基于阻抗控制的机器人柔顺性控制方法研究[D].南京：东南大学，2005.YANG Zhen.An Overview on Compliance Control of Robot Based on the Impedance Control[D].Nanjing：Southeast University，2005.

[12]温淑焕.机器人模糊神经网络阻抗控制[J].系统仿真学报，2004，16(11)：2614-2617.WEN Shuhuan.Fuzzy Neural Networks Impendence Control of Robot[J].Journal of System Simulation，2004，16(11)：2614-2617.

[13]陈贵亮，曹伟涛，杨 冬，等.基于阻抗控制的幕墙安装机器人柔顺操作研究[J].工程设计学报，2017，24(1)：100-107.CHEN Guiliang，CAO Weitao，YANG Dong，et al.Compliant Operation Research for Slabstone-Installing Robot Based on Impedance Control[J].Chinese Journal of Engineering Design，2017，24(1)：100-107.

[14]刘智光，于 菲，张 靓，等.基于模糊自适应阻抗控制的机器人接触力跟踪[J].工程设计学报，2015，22(6)：569-574.LIU Zhiguang，YU Fei，ZHANG Liang，et al.Force Tracking Research for Robot Based on Fuzzy Adaptive Impedance Control Algorithm[J].Chinese Journal of Engineering Design，2015，22(6)：569-574.