五自由度混联机构圆弧插补算法研究

王学雷 张 宾 徐松兵 李传军 吴泰羽 张春龙

(中国农业大学工学院， 北京 100083)

引言

并联机构具有结构简单、刚度大、承载能力大、误差小、动态响应性能好等优点而受到人们的青睐。但因其工作空间小、灵活性差等缺点而难以拓展到更为广阔的应用领域[1-4]。

传统生产线上的工业机器人多采用串联结构形式，这种拓扑结构决定了机器人在工作范围和姿态调整上具有较高的灵活性和柔性，但该种形式的机器人多采用悬臂梁式结构形式，冗长的悬臂结构使得机器人刚度差、负载能力和动态特性相当有限，且各关节的运动误差逐步累积并被放大，末端执行器很难达到较高的运动精度[5-8]。

混联机构结合串联机构和并联机构的优点，弥补了两者的不足而成为机构学领域的研究焦点[9-12]，最为典型的代表是瑞典NEUMANN博士发明的Tricept机器人[13]。国内学者也对五自由度混联机构进行了广泛研究，HUANG等[14-16 ]提出了TriVariant以及3SPR-RR五自由度混联机构，张东胜等[17]提出了2SPR/UPR-RP五自由度混联机构，上述混联机构分别以具有两转一移的并联机构2UPS/UP、3SPR以及2SPR/UPR为基础，串联一个具有两自由度摆头的串联机构组成；王书森等[18]提出了一种以四自由度并联机构2RPU/2UPS为主体，辅以一具有移动功能的直线导轨组成的五自由度混联机构，上述五自由度混联机构在实际生产中有着广泛的应用。

螺旋线为空间圆弧和与该圆弧平面垂直的直线运动的合成，相比直线插补算法，圆弧插补算法复杂得多，其中传统空间圆弧插补算法计算繁琐，工作量大[19-20]，因此对空间圆弧插补算法的研究极其重要。

本文在结合传统混联机构的基础上，设计一种由两自由度并联机构和三自由度串联机构构成的新型五自由度混联机构，并提出一种基于等弧度数据采样的新型空间圆弧插补算法。

1 五自由度混联机构构型

基于橡胶树割胶轨迹要求，本文提出由两自由度并联机构和三自由度串联机构构成的五自由度混联机构，如图1所示。

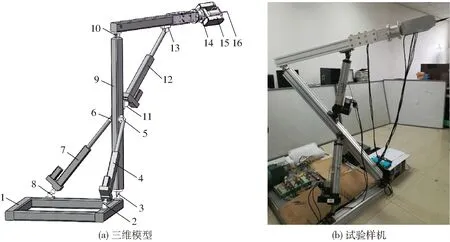
图1 五自由度混联机构Fig.1 5-DOF hybrid mechanism1.机座 2、8.球铰 3、5、6.虎克铰 9.大臂 4、7、12.电动缸 10、11、13、14、15.转动副 16.末端执行器

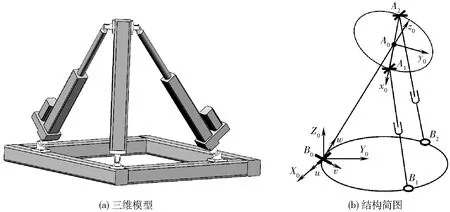
图2 两自由度并联机构Fig.2 2-DOF parallel mechanism

其中，两自由度并联机构由机座、2个结构完全相同的SPU(球副-移动副-虎克铰)型驱动分支以及1个U(虎克铰)型约束分支构成，可等效为2SPU+U并联机构，其三维模型以及结构简图如图2所示。通过控制2个 SPU驱动分支的长度即可实现该并联机构位姿的调整。

三自由度串联机构包括3个转动自由度，可等效为RRR串联机构。图1中转动副10由RPR (转动副-移动副-转动副) 型驱动分支驱动，该驱动分支两端为转动副11和13，分别与混联机构大臂和小臂相连，增加了RRR串联机构的刚度。

结合上述两自由度并联机构2SPU+U与三自由度串联机构RRR，该五自由度混联机构可等效为2SPU+U+RRR机构。

2 混联机构运动学分析

由上述五自由度混联机构结构图可知，2个SPU型驱动分支和一个RPR驱动分支分别驱动虎克铰3和转动副10，将上述3个驱动分支舍去，该混联机构便可等效为U+RRR五自由度串联机构，如图3所示。因此，对该混联机构的运动学分析可简化为对U+RRR串联机构的分析。

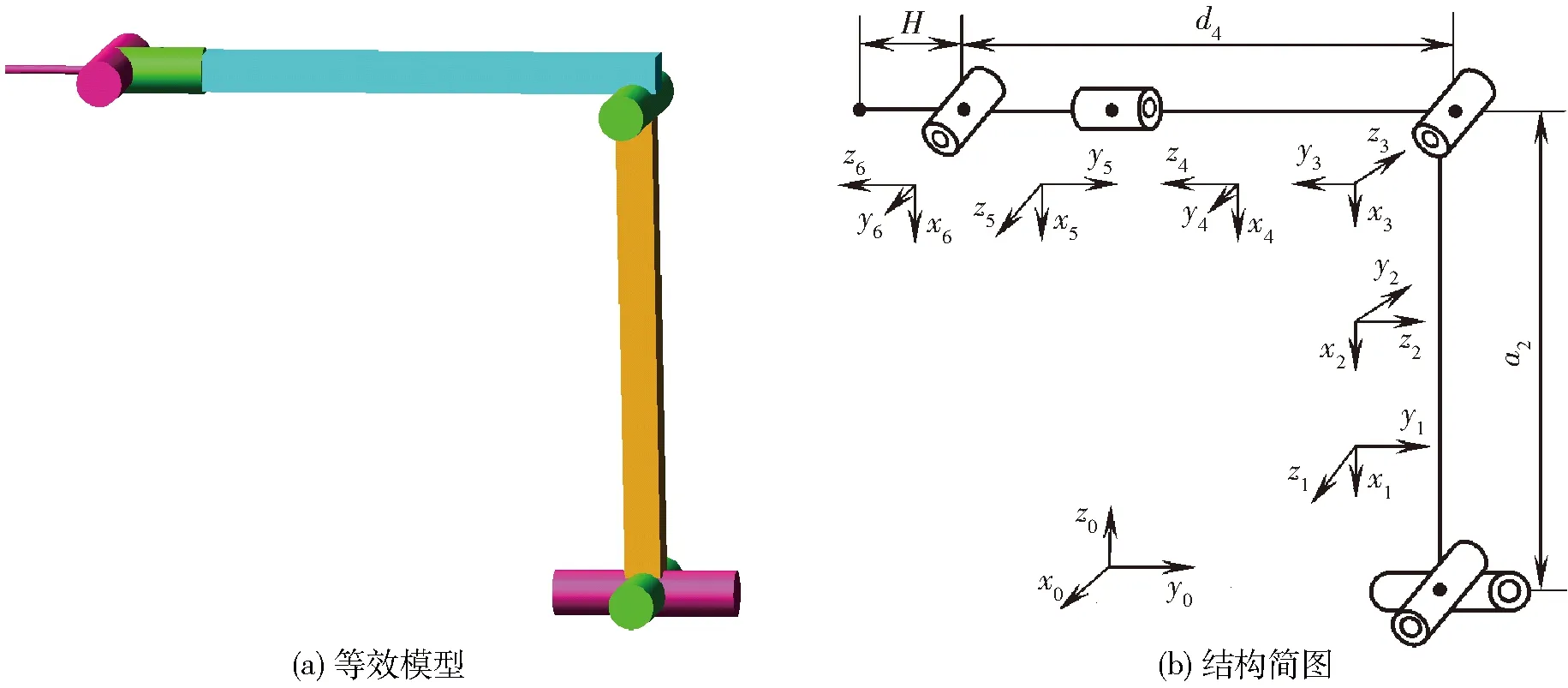
图3 U+RRR串联机构简图Fig.3 Schematic diagram of U+RRR series mechanism

串联机构的运动学分析有旋量理论[21]和D-H法[22-25]，由于D-H法可快速简洁地求出机械臂正、逆运动学表达式，故本文采用D-H法对该U+RRR机构进行运动学分析。通过图3可以看出该U+RRR串联机构具有5个旋转关节，各关节轴线之间互相垂直或平行，建立其连杆坐标系，各坐标系z轴与各关节轴线重合，如图3所示。其D-H参数如表1所示，其中，θi为连杆i绕关节i的Zi-1轴的转角；di为连杆i沿关节i的Zi-1轴的位移；ai为沿Xi方向上连杆i的长度；αi为连杆i两关节轴线之间的扭角。

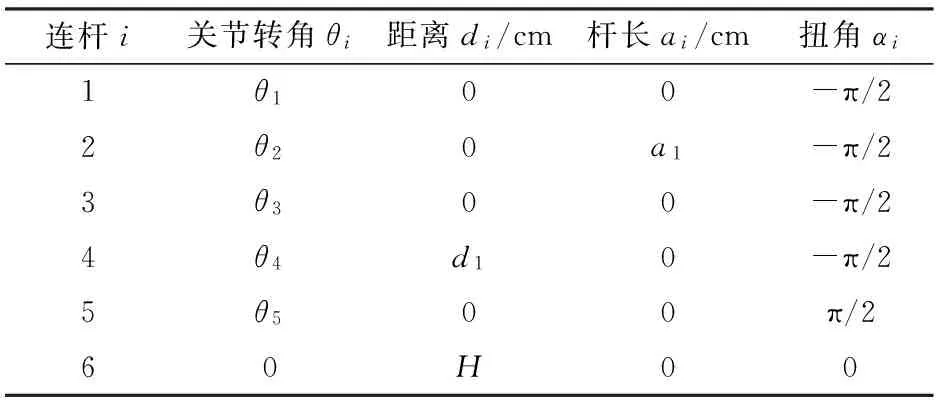
表1 U+RRR串联机构D-H参数Tab.1 D-H parameters of U+RRR series mechanism

2.1 U+RRR串联机构正向运动学分析

机器人正向运动是指给出机器人各连杆几何参数和各关节变量，求解机器人末端执行器在固定坐标系中的位置和姿态。根据连杆坐标系之间的齐次变换关系求出该五自由度串联机械臂相邻关节坐标系之间的齐次变换矩阵0T1、1T2、2T3、3T4、4T5、5T6为

机械臂末端执行器相对于基坐标系之间的齐次变换矩阵0T6可表示

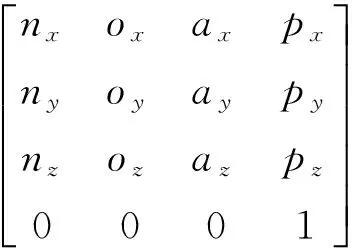
(1)

其中

nx=cθ5(cθ2sθ4-cθ3cθ4sθ2)-sθ2sθ3sθ5

ny=sθ5(cθ1cθ3+cθ2sθ1sθ3)-
cθ5(cθ4(cθ1sθ3-cθ2cθ3sθ1)-sθ1sθ2sθ4)
nz=sθ5(cθ3sθ1-cθ1cθ2sθ3)-
cθ5(cθ4(sθ1sθ3+cθ1cθ2cθ3)+cθ1sθ2sθ4)
ox=cθ2cθ4+cθ3sθ2sθ4
oy=sθ4(cθ1sθ3-cθ2cθ3sθ1)+cθ4sθ1sθ2
oz=sθ4(sθ1sθ3+cθ1cθ2cθ3)-cθ1cθ4sθ2
ax=sθ5(cθ2sθ4-cθ3cθ4sθ2)+cθ5sθ2sθ3
ay=-sθ5(cθ4(cθ1sθ3-cθ2cθ3sθ1)-sθ1sθ2sθ4)-
cθ5(cθ1cθ3+cθ2sθ1sθ3)
az=-sθ5(cθ4(sθ1sθ3+cθ1cθ2cθ3)+cθ1sθ2sθ4)-
cθ5(cθ3sθ1-cθ1cθ2sθ3)
px=Hsθ5(cθ2sθ4-cθ3cθ4sθ2)-a1sθ2+d1sθ2sθ3+
Hcθ5sθ2sθ3
py=a1cθ2sθ1-d1(cθ1cθ3+cθ2sθ1sθ3)-
Hsθ5(cθ4(cθ1sθ3-cθ2cθ3sθ1-sθ1sθ2sθ4))-
Hcθ5(cθ1cθ3+cθ2sθ1sθ3)pz=-d1(cθ3sθ1-cθ1cθ2sθ3)-a1cθ1cθ2-
Hsθ5(cθ4(sθ1sθ3+cθ1cθ2cθ3+cθ1sθ2sθ4))-
Hcθ5(cθ3sθ1-cθ1cθ2sθ3)

上式中，sθi=sinθi，cθi=cosθi，i=1,2，…,5。至此，该U+RRR串联机械臂运动学正解求解完毕。

2.2 U+RRR串联机构运动学反解分析

机器人逆运动学为正运动学的逆过程，即已知机器人末端执行器在基坐标系中的位置和姿态，求解相应的各关节变量，它是机器人运动控制和轨迹规划的基础，也是运动学的重要部分。本文采用解析法求解该U+RRR机械臂的逆解，求解过程如下：

(1)求解θ3

设该机械臂所期望的位姿为

0T6=0T11T22T33T44T55T6

(2)

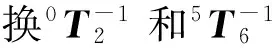
式(3)～(5)平方相加，化简得

(6)

即

(7)

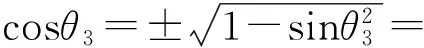
(8)

由式 (7)、(8)可得

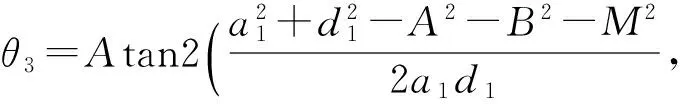
(9)

(2)求解θ2

由式(4)得

(10)

(11)

由式(10)、(11)可得

(12)

(3)求解θ1

由式(5)得

-Asinθ1+Bcosθ1=N

(13)

其中

N=-d1cosθ3

利用三角函数代换关系，引入中间变量r和φ，设

A=rcosφ

(14)

B=rsinφ

(15)

(16)

得

φ=Atan2(B,A)

(17)

则式 (13) 可转换为

(18)

利用三角函数和差化积公式，式(18)可转换为

(19)

(20)

则有

(21)

(4)求解θ4

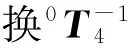
令L=Hcosθ4sinθ5，K=Hsinθ4sinθ5，式(23)与式(22)相除，化简得

θ4=Atan2(K,L)

(24)

(5)求解θ5

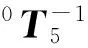
p65x=py[sinθ1(sinθ2sinθ4+cosζ2cosθ3cosθ4)-
cosθ1cosθ4sinθ3]+
px(cosθ2sinθ4-cosθ3cosθ4sinθ2)-
a1cosθ3cosθ4-pz[cosθ1(sinθ2sinθ4+
cosθ2cosθ3cosθ4)+cosθ4sinθ1sinθ3]=Hsinθ5

(25)

p65y=py(cosθ1cosθ3+cosθ2sinθ1sinθ3)+
pz(cosθ3sinθ3-cosθ1cosθ2sinθ3)+
d1-a1sinθ3-pxsinθ2sinθ3=-Hcosθ5

(26)

令W=Hsinθ5，G=-Hcosθ5，式(25)与式(26)相除，得

θ5=Atan2(W,-G)

(27)

至此，完成了对该U+RRR机械臂的逆运动学求解。

由式(9)、(12)、(21)可知，逆解θ1、θ2和θ3均存在正负2种可能解，因此该机械臂逆解具有多解性，即可以有多个位形来到达机械臂所要求的位姿，而对机械臂进行控制时，只需选择其中一个适合的解来处理。在实际应用中，一般根据最短行程原则从多组关节角中选出机械臂的最优解。最短行程原则是指选择与当前关节角差距最小的下一组解作为最优解，从而使两时刻之间关节运动距离最短，以减少机器人运动过程中能量的消耗。在关节角最优解选择过程中，一旦遇到有2个可能解，立刻应用最短行程原则进行判断，再利用新确定的最优解根据最短行程原则确定后续关节角，以此类推，每个关节只有一组关节角是合理的。最优解的确定流程如图4所示。

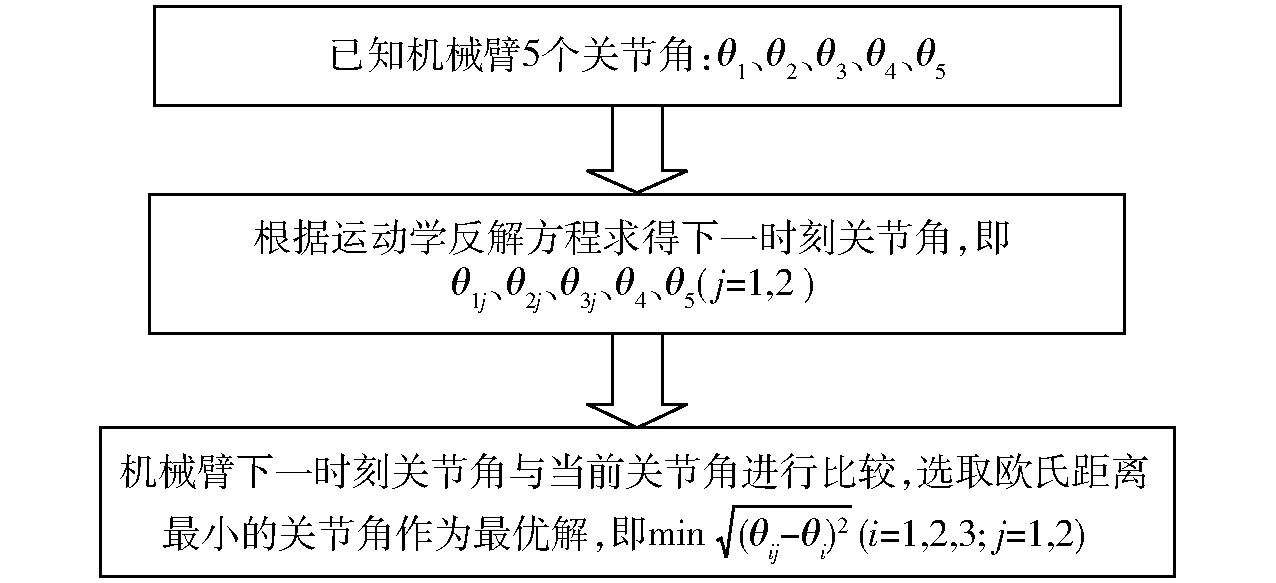
图4 机械臂逆解唯一性确定流程图Fig.4 Flow chart of inverse kinematics ascertain for robot arm

2.3 机械臂运动学正反解验证

为验证上述机械臂运动学正反解求解的正确性，设机械臂末端执行器沿一直线运动，直线的起始点、中间点和终止点坐标分别为ps=(0,-89,132)、pm=(10,-94,137)和pe=(20,-99,142)，运动过程中其末端执行器z轴姿态始终为a=(ax,ay,az)=(0,-1,0)。以机械臂在直线起始点、中间点和终止点时正反解为例，在Matlab中编写程序对正反解正确性进行验证，验证流程如图5所示。

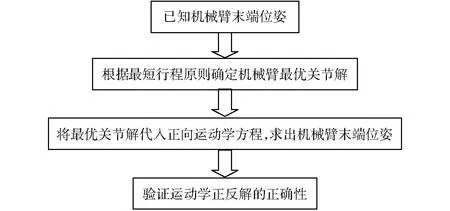
图5 机械臂运动学正反解验证流程图Fig.5 Verification flow chart of inverse/forward kinematics for robot arm

根据图4所示流程图求出机械臂在直线起始点、中间点和终止点时最优关节角，如表2所示。将表2中求得的3组机械臂最优关节角代入运动学正解方程式(1)中，求得机械臂末端位置和姿态，如表3所示。

表2 U+RRR 机械臂逆解求解Tab.2 Inverse kinematics of U+RRR series mechanism

表3 U+RRR机械臂正解求解Tab.3 Forward kinematics of U+RRR series mechanism

从表2和表3可以看出，表3中机械臂3组最优关节角对应的末端执行器位置和姿态与表2中机械臂3组关节角对应的位置和姿态完全一致，说明运动学正反解的正确性。

2.4 2SPU+U并联机构运动学分析

当求出上述U+RRR串联机械臂θ1、θ2后，通过坐标变换可求出并联机构两电动缸的长度与θ1、θ2的关系。

在静平台B0点建立固定坐标系B0X0Y0Z0与动坐标系B0uvw，X0轴与约束支链上虎克铰U的固定转动轴轴线重合，Z0轴与静平台垂直，Y0轴根据右手定则确定；u轴与X0轴重合，w轴沿B0A0方向，v轴根据右手法则确定，在A0点建立动坐标系A0x0y0z0，x0轴为从点A0指向点A1的方向，z0轴沿B0A0方向，y0轴根据右手法则确定，如图2所示。初始时刻固定坐标系B0X0Y0Z0与动坐标系B0uvw重合，机构动、静平台平行，且θ1=0，θ2=0，动坐标系A0x0y0z0在固定坐标系B0X0Y0Z0中位置为(0,0,Z)，其中，Z为动平台与固定平台的初始距离。Bi(i=0,1,2)在固定坐标系B0X0Y0Z0中坐标为

(28)

点Ai(i=0,1,2)在动坐标系A0x0y0z0中位置为

(29)

设动平台首先绕u轴旋转θ1，然后绕v轴旋转θ2，由于所有变换矩阵均相对运动坐标系B0uvw进行，根据“从左向右”计算原则，得相应的齐次变换矩阵为

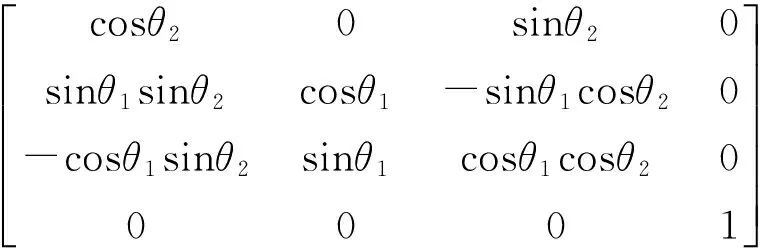
此时，动平台上Ai(i=0,1,2) 点在固定坐标系B0X0Y0Z0中的位置可表示为

(30)

式中TZ——初始时刻动平台相对于固定坐标系的齐次变换矩阵

则SPU驱动分支的长度可表示为

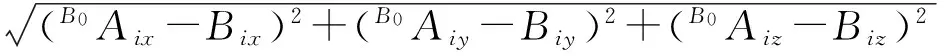
(31)

3 空间圆弧插补算法研究

提出了一种基于等弧度数据采样的空间圆弧插补算法，该方法对圆弧路径进行等弧度离散分割，再对分割后的圆弧进行粗插补，不需求解圆弧所在的平面方程，也无需坐标转换，简化了插补算法的计算量。对于圆心角θ，需考虑0<θ≤π和π<θ<2π两种情况。

图6 空间圆弧插补原理Fig.6 Interpolation principle of space arc

(1)对于圆心角0<θ≤π的情况

设给定圆弧上起始点ps=(xs,ys,zs)、终止点pe=(xe,ye,ze)以及圆弧圆心p0=(x0,y0,z0)，设圆弧半径为R，则有

lp0ps=lp0pe=R

(32)

现根据起始点ps、终止点pe以及圆心p0求取圆弧上插补点pi的位置坐标，如图6a所示。首先从起始点ps到终止点pe对圆弧进行等弧度分割，弧长的分割精度为ΔL，由于弧长与其圆心角有关，故采取对圆心角等角度细分的方法对圆弧进行等弧度细分，根据分割弧长ΔL计算完成整个圆弧轨迹所需的插补次数n，再计算圆弧上第j个插补点的坐标pj，具体计算过程如下：

通过起始点ps和终止点pe的位置坐标可计算出弦pspe的长度L，即

(33)

根据半径R及弦长L计算圆心到弦pspe的距离H，即

(34)

根据半径R以及圆心角计算圆弧pspe的长度K为

K=Rθ

(35)

根据圆弧分割精度ΔL计算圆弧插补次数n为

(36)

设第j个插补点为pj，其与圆心p0的连线与弦pspe相交于点p′j，则psp′j的长度为

(37)

点p′j的坐标为

(38)

直线p0p′j的长度为

(39)

因点p0、p′j和pj共线，进而求得插补点pj的坐标为

(40)

(2)对于圆心角π<θ<2π的情况

圆弧pspe对应圆心角π<θ<2π的情况如图6b所示，欲求圆弧pspe上的插补点pj，可延长直线psp0与圆弧交于点p′s，延长直线pep0与圆弧交于点p′e，此时，圆弧pspe被分为圆弧psp′e、圆弧p′ep′s以及圆弧p′spe，上述每段圆弧所对应的圆心角均小于π，故对每段圆弧可采用圆心角0<θ≤π对应的情况进行插补点的计算，在此不再叙述。

根据以上推导可求出每个插补点pj的位置坐标，对机器人在这些插补点的位置进行逆解计算，便可求出机器人各驱动关节所需的位移。

4 空间圆弧插补算法验证

4.1 圆弧插补算法Matlab仿真验证

(1) 对圆心角0<θ≤π的情况进行Matlab仿真：设圆弧的起始点、终止点和圆心坐标分别为ps=(0,-89,142)、pe=(10,-89,132)和p0=(10,-89,142)。设圆弧分割精度为ΔL=0.1 mm，在Matlab中编写圆弧插补算法程序，绘制的圆弧轨迹如图7a所示。

图7 空间圆弧插补轨迹图Fig.7 Track charts of space arc interpolation

(2) 对圆心角π<θ<2π的情况进行圆弧Matlab仿真：设圆弧的起始点、终止点和圆心坐标分别为ps=(10,-89,132)、pe=(0,-89,142)和p0=(10,-89,142)。直线psp0延长线与圆弧交点坐标为p′s=(10,-89,152)，直线pep0延长线与圆弧交点坐标为p′e=(20,-89,142)，在Matlab中编写圆弧插补算法程序，绘制的圆弧轨迹如图7b所示。

(3) 绘制一个整圆：取上述圆弧圆心角0<θ≤π与圆心角π<θ<2π两种情况相同的起始点、终止点和圆心坐标点，在Matlab中编写绘制整圆的圆弧插补算法程序，绘制的圆弧轨迹如图7c所示。

4.2 插补算法试验样机验证

为对上述圆弧插补算法进行验证，基于提出的2SPU+U+RRR五自由度混联机构，搭建实验样机，控制系统采用“运动控制卡(DSP28335) + PC机”的方法，以PC机作为上位机，运动控制卡 (DSP28335) 作为下位机，由DSP28335控制器完成控制信号的生成，采用毛笔在白纸上画出圆弧轨迹的方法对上述圆弧插补算法进行验证。通过TI公司提供的CCS5.5编译软件对该混联机构运动控制程序进行编译处理，实现对机构的运动控制。

通过上述圆弧插补算法可得圆弧的实时插补坐标，图8为该混联机构所画的圆弧轨迹。其中，图8a为圆弧圆心角0<θ≤π，圆弧的起始点、终止点和圆心坐标分别为ps=(0,-89,142)、pe=(10,-89,132)和p0=(10,-89,142)所对应的空间圆弧；图8b为圆弧圆心角π<θ<2π，且圆弧的起始点、终止点和圆心坐标分别为ps=(10,-89,132)、pe=(0,-89,142)和p0=(10,-89,142)所对应的空间圆弧；图8c为上述两个圆弧合并成整圆。

图8 圆弧插补实验Fig.8 Experiment pictures of space arc interpolation

由图8可以看出，所画的圆弧轨迹平滑，衔接紧密，笔画清晰，验证了上述圆弧插补算法的正确性。

5 结论

(1)提出了一种由两自由度并联机构和三自由度串联机构构成的五自由度混联机构，其中，两自由度并联机构增加机构的承载能力和刚度，三自由度串联机构增加机器人的刚度、灵活性和工作空间，相对传统混联机构，该机构具有更大工作空间和更高刚度。

(2)将五自由度混联机构等效为U+RRR串联机构，对串联机构进行运动学正反解分析，确定了逆解唯一解的选取原则，并验证了运动学正反解解析表达式的正确性。根据得到的虎克铰U两轴线转动角度θ1、θ2，通过坐标转换求得了两驱动分支SPU杆长的表达式，为机构的运动控制奠定理论基础。

(3)为满足对工件复杂曲面的加工需要，提出了一种基于等弧度数据采样的新型空间圆弧插补算法，该方法对圆弧路径进行等弧度离散分割，直接在笛卡儿坐标系中进行，无需坐标转换，简化了插补算法的计算量，通过Matlab仿真和样机实验验证了该方法的正确性。

1 MENG X D, GAO F, WU S F. Type synthesis of parallel robotic mechanisms: framework and brief review [J]. Mechanism and Machine Theory, 2014, 78: 177-186.

2 LIM H, LEE S H, SO B R, et al. Design of a new 6-DOF parallel mechanism with a suspended platform [J]. International Journal of Control, Automation, and Systems, 2015, 13(4): 942-950.

3 PLITEA N, SZILAGHYI A, PISLA D. Kinematic analysis of a new 5-DOF modular parallel robot for brachytherapy [J]. Robotics and Computer-Integrated Manufacturing, 2015, 31: 70-80．

4 耿明超, 赵铁石, 王唱, 等. 4-UPS/UPR并联机构动力学分析 [J/OL]. 农业机械学报, 2014, 45(8): 299-306.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20140848&flag=1.DOI:10.6041/j.issn.1000-1298.2014.08.048.

GENG Mingchao, ZHAO Tieshi, WANG Chang, et al. 4-UPS /UPR parallel mechanism dynamic analysis [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(8): 299-306. (in Chinese)

5 DU X D, SHAO H K, CHEN Y J, et al. An online method for serial robot self-calibration with CMAC and UKF [J]. Robotics and Computer-Integrated Manufacturing, 2016, 42: 39-48.

6 MUSTAFA A, KERIM C, SHI Z P, et al. Comparison of four different heuristic optimization algorithms for the inverse kinematics solution of a real 4-DOF serial robot manipulator [J]. Neural Computing and Applications, 2016, 27: 825-836.

7 王梦, 付铁, 丁洪生，等. 7自由度串联机器人运动学分析[J]. 机械设计与制造, 2016(8): 8-11.

WANG Meng, FU Tie, DING Hongsheng, et al. Kinematics analysis of a 7-DOF serial robot [J]. Machinery Design and Manufacture, 2016(8): 8-11. (in Chinese)

8 田海波, 马宏伟, 魏娟. 串联机器人机械臂工作空间与结构参数研究 [J/OL]. 农业机械学报, 2013, 44(4): 196-201.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130434&flag=1.DOI:10.6041/j.issn.1000-1298.2013.04.034.

TIAN Haibo, MA Hongwei, WEI Juan. Workspace and structural parameters analysis for manipulator of serial robot [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(4): 196-201. (in Chinese)

9 LU Y, DAI Z H, YE N J. Dynamics analysis of novel hybrid robotic arm with three fingers [J]. Robotica, 2016, 34(12): 2759-2775.

10 GUO W J, LI R F, CAO C Q. Kinematics, dynamics, and control system of a new 5-degree-of-freedom hybrid robot manipulator [J]. Advances in Mechanical Engineering, 2016, 8(11): 1-19.

11 ZHOU H, QIN Y, CHEN H, et al. Structural synthesis of five-degree-of-freedom hybrid kinematics mechanism [J]. Journal of Engineering Design, 2016, 27(4-6): 390-412.

12 曹毅, 秦友蕾, 陈海, 等. 基于GF集理论的五自由度混联机器人构型综合[J/OL]. 农业机械学报, 2015, 46(11): 392-398. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20151153&flag=1. DOI: 10.6041/j.issn.1000-1298.2015.11.053.

CAO Yi, QIN Youlei, CHEN Hai, et al. Structural synthesis of 5-DOF hybrid mechanisms based on GF set [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(11): 392-398. (in Chinese)

13 盛东义, 赵勇, 王皓, 等. Tricept 并联机构的弹性动力学性能[J]. 机械设计与研究, 2012, 28(6): 23-29.

SHENG Dongyi, ZHAO Yong, WANG Hao, et al. Kineto-elastic-dynamics (ked) analysis of Tricept parallel mechanism [J]. Machine Design and Research, 2012, 28(6): 23-29. (in Chinese)

14 HUANG T, LI T M, ZHAO X M, et al. Conceptual design and dimensional synthesis for a 3-DOF module of the TriVariant-a novel 5-DOF reconfigurable hybrid robot [J]. IEEE Transactions on Robotics, 2005, 21(3): 449-456．

15 LIU H T, HUANG T, ZHAO X M, et al. Optimal design of the TriVariant robot to achieve a nearly axial symmetry of kinematic performance [J]. Mechanism and Machine Theory, 2007, 42(12): 1643-1652.

16 李彬, 黄田, 张利敏, 等. 一种新型五自由度混联机械手的概念设计及尺度综合[J]. 中国机械工程, 2011, 22(16): 1900-1905.

LI Bin, HUANG Tian, ZHANG Limin, et al. Conceptual design and dimensional synthesis of a novel 5-DOF hybrid manipulator [J]. China Mechanical Engineering, 2011, 22(16): 1900-1905. (in Chinese)

17 张东胜, 许允斗, 赵永生, 等. 五自由度混联机器人逆动力学分析 [J/OL]. 农业机械学报, 2017, 48(9): 384-391.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20170949&flag=1.DOI:10.6041/j.issn.1000-1298.2017.09.049.

ZHANG Dongsheng, XU Yundou, ZHAO Yongsheng, et al. Inverse dynamic analysis of novel 5-DOF hybrid manipulator [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(9): 384-391. (in Chinese)

18 王书森, 梅瑛, 李瑞琴. 新型3T2R龙门式混联机床动力学模型[J]. 机械工程学报, 2016, 52(15): 81-90.

WANG Shusen, MEI Ying, LI Ruiqin. Solving dynamics for a novel 3T2R gantry hybrid machine tool [J]. Journal of Mechanical Engineering, 2016, 52(15): 81-90. (in Chinese)

19 高宏卿, 宾鸿赞. 空间圆弧变换插补原理与算法[J]. 组合机床与自动化加工技术,1993(3): 2-6.

GAO Hongqing, Bin Hongzan. Theory and algorithm of space circular are transformation interpolation [J]. Modular Machine Tool and Automatic Manufacturing Technique, 1993(3): 2-6. (in Chinese)

20 王忠平, 田作华. 基于矢量的DDA 空间圆弧插补算法[J]. 机械设计与制造, 2007(9): 164-165.

WANG Zhongping, TIAN Zuohua. DDA 3D circular interpolation based on vector [J]. Machinery Design and Manufacture, 2007(9): 164-165. (in Chinese)

21 李盛前, 谢小鹏. 基于旋量理论和Sylvester 结式法的6 自由度机器人逆运动学求解分析[J]. 农业工程学报, 2015, 31(20): 48-54.

LI Shengqian, XIE Xiaopeng. Analysis of inverse kinematic solution for 6R robot based on screw theory and Sylvester resultant [J]. Transactions of the CSAE, 2015, 31(20): 48-54. (in Chinese)

22 李国利, 姬长英, 顾宝兴, 等. 多末端苹果采摘机器人机械手运动学分析与试验[J/OL].农业机械学报,2016,47(12):14-29. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20161203&flag=1.DOI:10.6041/j.issn.1000-1298.2016.12.003.

LI Guoli, JI Changying, GU Baoxing, et al. Kinematics analysis and experiment of apple harvesting robot manipulator with multiple end-effectors [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(12): 14-29. (in Chinese)

23 高艺, 马国庆, 于正林, 等. 一种六自由度工业机器人运动学分析及三维可视化仿真[J].中国机械工程, 2016, 27(13): 1726-1731.

GAO Yi, MA Guoqing, YU Zhenglin, et al. Kinematics analysis of an 6-DOF industrial and 3D visualization simulation [J]. China Mechanical Engineering, 2016, 27(13): 1726-1731. (in Chinese)

24 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006.

25 熊有伦. 机器人技术基础[M]. 武汉: 华中科技大学出版社, 2011.