12-6台体型Stewart冗余并联机构正向运动学研究

尤晶晶 符周舟 吴洪涛 李成刚 周 为

(1.南京林业大学机械电子工程学院， 南京 210037； 2.南京林业大学汽车与交通工程学院， 南京 210037；3.南京航空航天大学机电学院， 南京 210016； 4.江苏省精密与微细制造技术重点实验室， 南京 210016)

引言

1965年，英国工程师STEWART[1]在进行飞行模拟器的研究中首次提出一种含6条相同支链的并联机构。与串联机构相比，并联机构具有结构紧凑、输出精度高、动态特性好、承载能力强等特点[2]，这些优点使其能够适用于光学望远镜中主镜和副镜的位姿调整[3]、主从遥操作中手控器的驱动[4]、精密仪器中六维振动的传感[5]及隔离[6]等场合。然而，在实际应用中，六自由度并联机构的实时反馈控制一般很难实现，这限制了执行器的工作精度和效率，严重影响了进一步的推广应用。究其原因，由于多输入、多输出量的强耦合性，六自由度并联机构的正向运动学问题[7]最终归结为多元非线性方程组的求解，这个过程极其复杂，是继空间6R串联机器人位移分析完成后的又一机构学难题。

Stewart机构是六自由度并联机构中最基本的构型[8]，主要包括平台型和台体型两大类，它们的正向运动学问题引起了众多学者的广泛关注。从研究方法上看，主要有数值法和解析法两种。数值法的优点是省去了对约束方程的繁琐的消元处理过程，直接运用Newton-Raphson等数值逼近的思路[9-11]求解非线性方程组；然而，这种方法不能得到全部解，且初值选取及搜索算法对收敛性、效率、精度的影响较大，同时不利于速度、加速度的分析。因此，目前以解析法为主。文献[12]针对6-6平台型Stewart机构，运用分次字典序Groebner基法消元，得到一元20次方程；文献[13]针对6-3平台型Stewart机构，运用正交补法消元并舍弃系数较小的高次项，得到一元8次方程；文献[14]针对6-6台体型Stewart机构，运用共形几何代数建立运动学方程，并运用Grobner基法消元，得到一元40次方程；文献[15]针对6-4台体型Stewart机构，构造10阶Sylvester结式，得到一元32次方程；文献[16]针对5-5台体型Stewart机构，构造8阶Dixon结式，得到一元40次方程。以上算法的基本思路是一致的，即通过各种消元法，将多元非线性方程组转换成仅含单变量的一元高次方程。然而，获得的高次方程仍需要通过数值法求解，并没有实现运动学正解的全解析化，依然存在计算耗时及失根等问题。

文献[17]研究发现，并联机构正向运动学求解难易性与机构的耦合度指标有关，并指出，耦合度越低则正向运动学的解算越简单，且通过综合低耦合度的拓扑构型可能会得到其全解析解。文献[18]设计了一种零耦合度的9-3台体型Stewart冗余并联机构，运用“三点法”推导出了正向运动学的全解析解。然而，该机构中存在3个三重复合球面副，故面临制造、装配等难题。本文在此基础上，提出一种不含三重复合球面副的12-6台体型Stewart冗余并联机构，首先，运用方位特征集理论计算基本运动链(Basic kinematic chain, BKC)及机构的耦合度；接着，在惯性系内推导并联机构正向运动学的全解析解，并对机构位姿求解的相容性条件以及角速度求解时可能出现的特殊情况进行分析；最后，通过虚拟实验对正解算法的正确性和实时性进行验证。

1 拓扑构型分析

图2 12-6台体型Stewart冗余并联机构拓扑构型Fig.2 Topological configuration of general 12-6 Stewart redundant parallel mechanism

12-6台体型Stewart冗余并联机构的结构模型及拓扑构型分别如图1、2所示。该机构由1个动平台、1个静平台以及6个完全相同的混合单开链支路(记为HSOC支路)构成。其中，HSOC支路是在传统“3S-2P”[19]空间五杆回路的顶端球面副上再串联连接1个同心的球面副形成的，6个二重复合球面副分别固结在立方体状动平台的6条棱边的中点。初始状态下，所有支链的长度相等，动平台位于静平台的几何中心处，其6个面分别与静平台的6个面平行。图2中，实心圆圈Bi、空心圆圈bi、“U型”连接件pi分别代表第i个二重复合球面副、一般球面副和移动副。

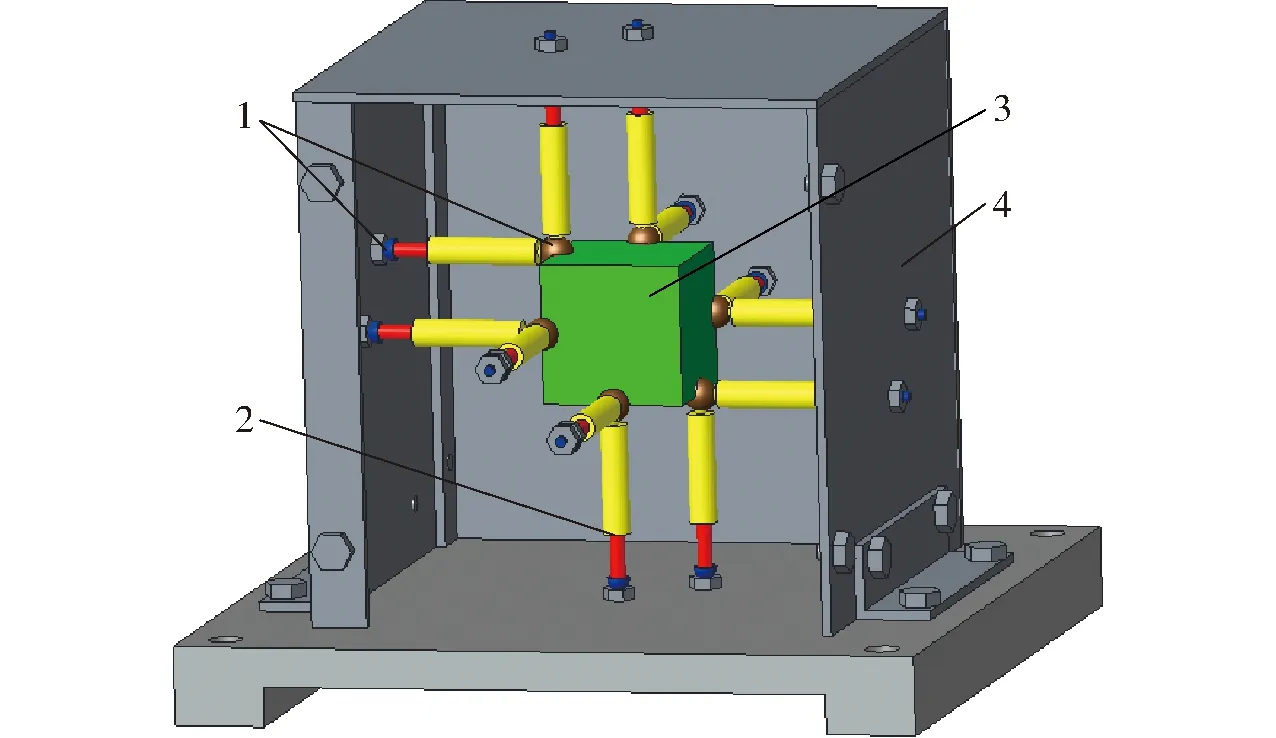
图1 12-6台体型Stewart冗余并联机构结构模型Fig.1 Structure model of general 12-6 Stewart redundant parallel mechanism1.球面副 2.移动副 3.动平台 4.静平台

以支路拓扑结构的基本类型来划分[17]，该机构本质上属于6-HSOC{-(R(3S-2P)-P(3S-2P)-P(3S-2P))-S-}型。因此，动平台的方位特征集就是6个HSOC支路末端构件的方位特征集的交集，即

(1)

式中Mp——动平台的方位特征集

Mi——第i个HSOC支路的方位特征集

t3、r3——相对于惯性参考系，构件存在的三维独立移动和三维独立转动

机构自由度为

D=dim.(Mp)=6

(2)

式中 dim.——方位特征集的维数

根据单开链(记为SOC)单元的机构组成原理[20]，11个独立回路的独立位移方程数为

ξi=6 (i=1,2,…,11)

(3)

式中ξi——第i个独立回路的位移方程数

根据机构拓扑结构的分解算法[20]，确定SOC分解路线。首先，取SOC1{-b1-p1-B1-p2-b2-},并结合式(3)，计算约束度为

(4)

式中m1——SOC1的运动副数

fi——第i个运动副的自由度(不包含局部自由度)

I1——SOC1的驱动副数

根据基本运动链的判定方法[20]，SOC1满足约束度的“最小划分”条件，对应于第1个BKC，可以计算其耦合度为

(5)

然后，取SOC2{-b3-p3-B2-p4-b4-}、SOC3{-b5-p5-B3- p6-b6-}，对应于第2、3个BKC，同理可得

k2=k3=0

(6)

分别将b1、b2连线和b3、b4连线的转轴记为R(b1-b2)、R(b3-b4)。取SOC4{-R(b1-b2)-B1-B2-R(b3-b4)-}, 其约束度为

(7)

取SOC5{-R(B1-B2)-B3-R(b5-b6)-},其约束度为

(8)

第4个BKC的耦合度为

(9)

进一步地，取SOC6{-b7-p7-B4-}、SOC7{-b8-p8- B4-}、SOC8{-b9-p9-B5-}、SOC9{-b10-p10-B5-}、SOC10{- b11-p11-B6-}、SOC11{-b12-p12-B6-},它们的约束度以及对应BKC的耦合度为

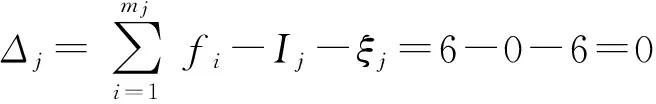
(10)

(11)

考虑到耦合度是BKC的一种拓扑不变量[21]，故在机构的工作空间中，10个BKC的耦合度均保持不变。这样，整个机构的耦合度k也是恒定值，即

k=max(k1,k2,…,k10)=1

(12)

式(12)显示，新型拓扑结构的耦合特性表现为弱耦合，表明每个回路的变量不能独立求出，需要将多个回路方程联立求解，这为构建并联机构的正向运动学模型指明了方向。

2 正向运动学模型

并联机构的“正向运动学”指的是：已知支链的输入驱动量，求解动平台的输出运动参数，包括位姿、速度等信息。

2.1 位姿正解

在静平台上固连惯性系{X-Y-Z}，如图2所示，坐标原点位于初始状态下的动平台中心处。这样，静平台上12个一般球面副的坐标可以统一成矩阵形式

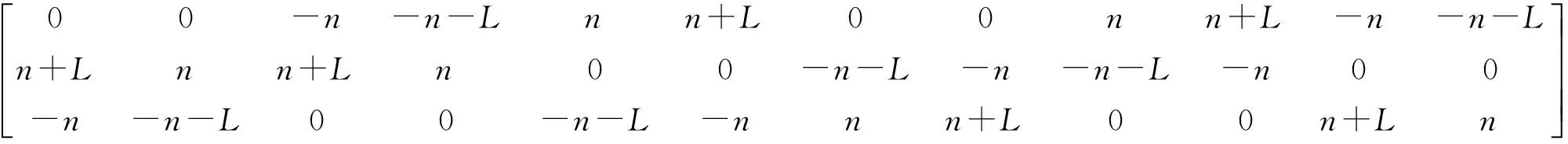
(13)

式中b1～b12——同名点的几何中心在惯性系内的笛卡尔坐标

n——动平台半边长

L——支链初始长度

将动平台的中心记作M，由机构的拓扑构型可知，M与B1～B6之间满足一定的几何关系，如图3所示。

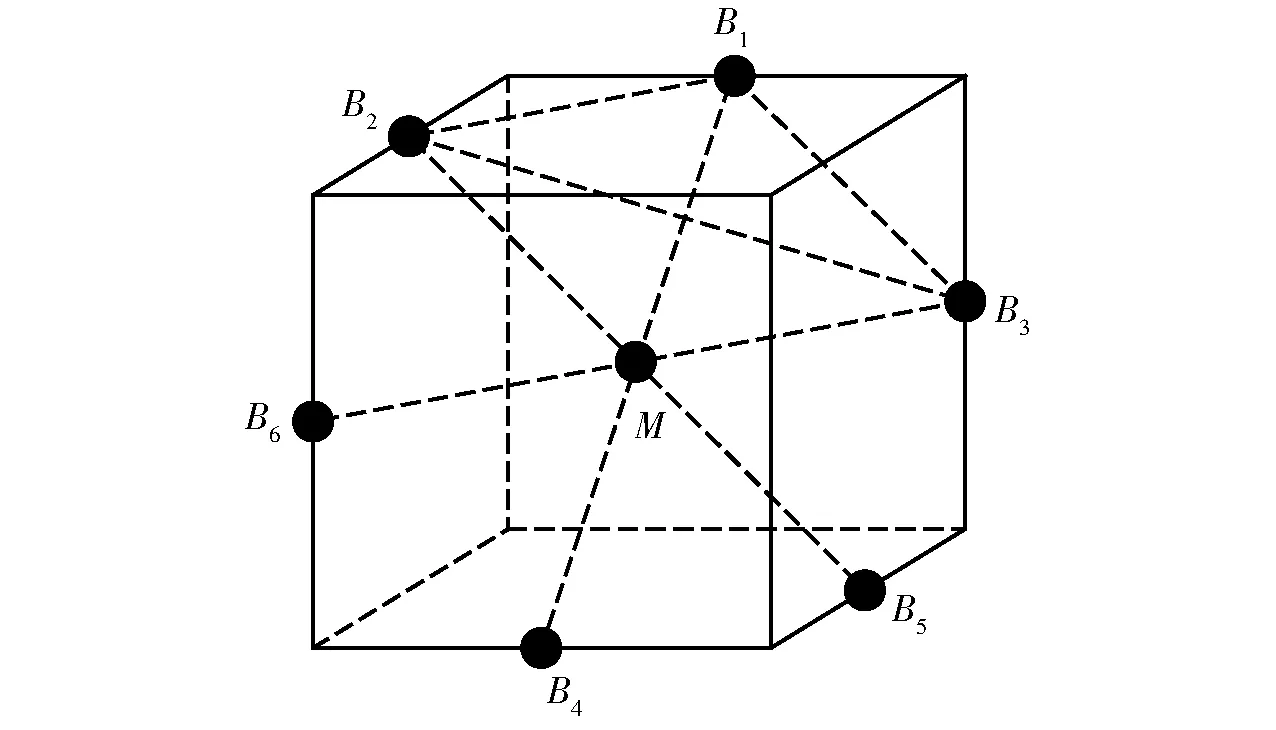
图3 动平台中心与复合球面副中心之间的几何关系Fig.3 Geometric relations between centers of moving platform and compound spherical pairs

运用立体几何知识容易证明出，3条线段B1B4、B2B5、B3B6的中点重合于点M；4个点B1、B2、M、B3位于同一平面上，且构成一个菱形。因此，这7个特征点的坐标之间满足

B1+B4=B2+B5=B3+B6=2M

(14)

B1+M=B2+B3

(15)

(16)

式中B1～B6、M——同名点的几何中心在惯性系内的笛卡尔坐标

|·|——矢量的模

动平台的位姿可以用B1、B2、B3、M点的坐标来描述，将它们视为待求量

(17)

根据12条支链的长度约束关系结合式(13)～(17)，建立并联机构输入、输出量集合中的位姿映射方程组

(18)

(19)

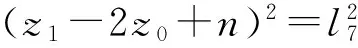
(20)

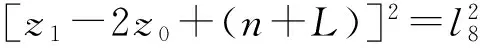
(21)

(x1-x0)2+(y1-y0)2+(z1-z0)2=2n2

(22)

(23)

(24)

(25)

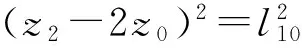
(26)

(x2-x0)2+(y2-y0)2+(z2-z0)2=2n2

(27)

(28)

(29)

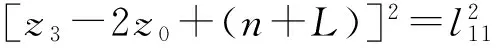
(30)

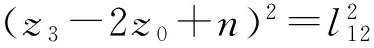
(31)

(x3-x0)2+(y3-y0)2+(z3-z0)2=2n2

(32)

式中li——第i条支链的长度，在正向运动学模型中为已知量

由式(18)～(32)可知，15个二次相容方程中存在若干对同构关系[22]；进一步分析后发现，同构方程两两相减，能够消去二次项，得到四组线性封闭方程

(33)

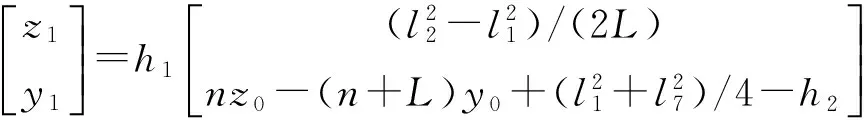
(34)

(35)

(36)

其中

再结合式(15)，得到剩余3个未知量的解析式

x1=x2+x3-x0

(37)

z2=z1-z3+z0

(38)

y3=y1-y2+y0

(39)

至此，解决了新型并联机构的位姿正解问题，具体算法流程如图4所示。其中，虚线框中的变量为已知量，实线框中的变量为待求量。

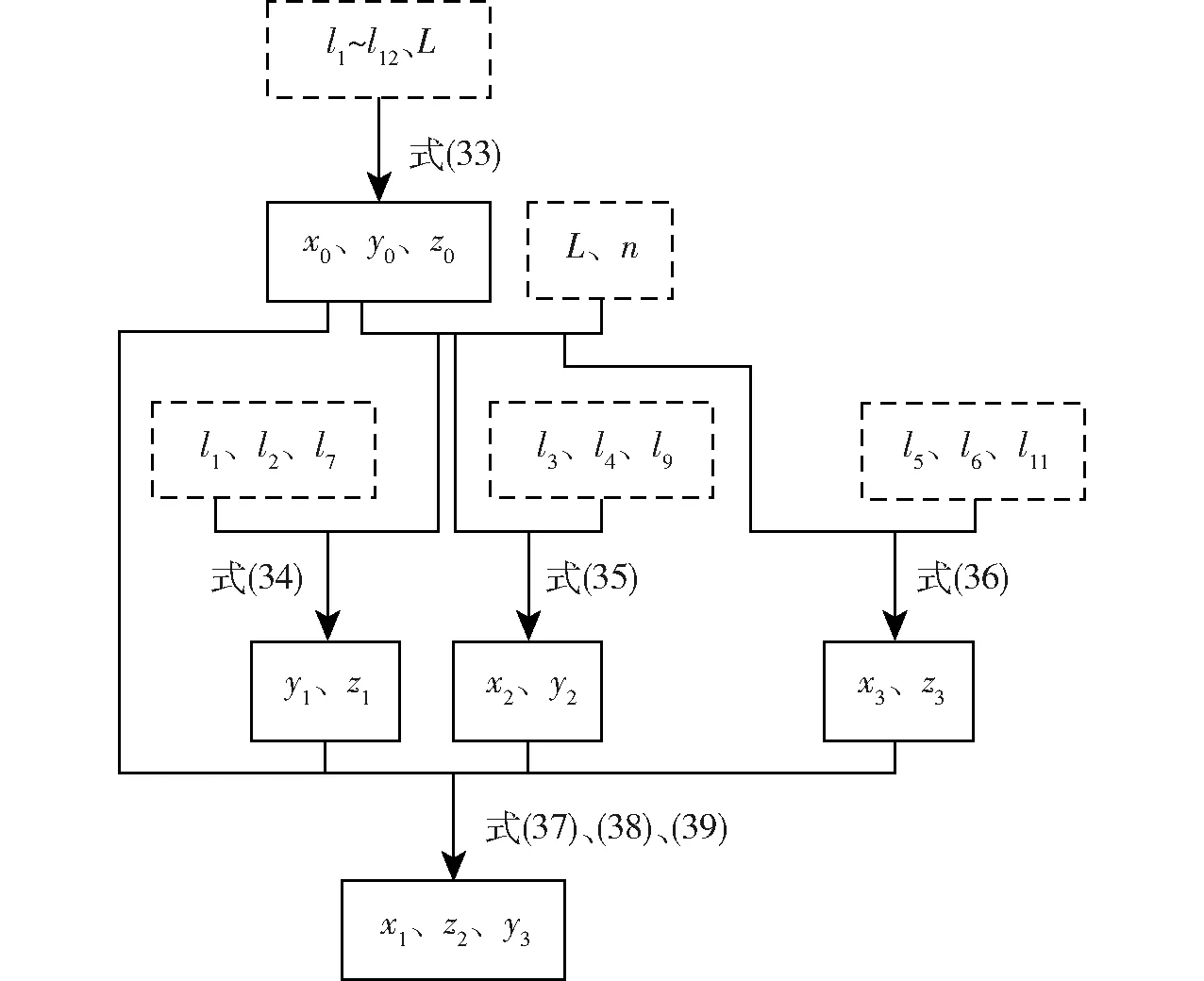
图4 位姿正解的算法流程Fig.4 Algorithm flow chart of forward displacement analysis

由图4可知：

(1)尽管本机构在结构上弱耦合，但由于其拓扑构型的冗余性和对称性，仍然存在确定的、唯一的、全解析形式的位姿正解，这为后续的实时反馈控制提供了有利条件。

(2)本机构的动平台位姿信息中，每一个特征量均与所有支链的长度有关，且关联程度高，表现为输入-输出运动的强耦合特性，故对驱动输入精度的要求较高。关于输出量对输入量的误差敏感度及误差传递模型，将另文推导。

2.2 杆长协调方程

将动平台视作刚性结构，运动过程中特征点之间的相对距离保持不变。因此，2.1小节中求解了的12个未知量之间除了满足式(22)、(27)、(32)的3个关系之外，还满足如下3个约束方程

(x1-x2)2+(y1-y2)2+(z1-z2)2=2n2

(40)

(x2-x3)2+(y2-y3)2+(z2-z3)2=6n2

(41)

(x1-x3)2+(y1-y3)2+(z1-z3)2=2n2

(42)

将式(33)～(39)的解析结果代入式(22)、(27)、(32)、(40)～(42)中并展开，得到12-6台体型Stewart冗余并联机构的杆长协调方程。一般情况下，协调方程的结构较为冗长，限于篇幅，这里不列出具体展开式。特殊地，当所有支链均采用微幅驱动时，杆长变化量的二次项可以忽略，此时，杆长协调方程可以近似展开成

(43)

可见，该并联机构的12条杆长(输入量)之间并不是完全独立的；任意给定N(6≤N≤11)条杆长，可通过解析或数值的方法计算出其他(12-N)条杆长。

容易证明出，当并联机构的12条杆长同时满足6个杆长协调方程时，其正向运动学方程组满足相容性条件。此时，方程组的解的个数至少为1，因此，按照图4算法得到的正解中一定没有增根。另一方面，四组线性封闭方程(33)～(36)是通过将15个二次相容方程(18)～(32)两两相减(求交集)获得的，即前者的解一定包含了后者的解，因此，上述正解中也一定不会出现失根的情况。

2.3 速度正解

将式(33)等号两边同时对时间求一阶导数，得到动平台中心线速度v的解析式(唯一解)

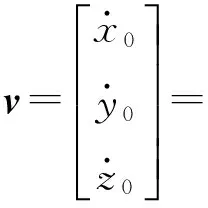
(44)

分别将式(34)～(36)的等号两边对时间求一阶导数，整理后提取出其中的3个变量解析式

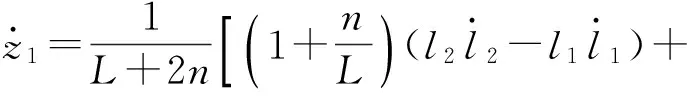
(45)

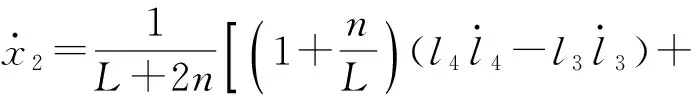
(46)

(47)

根据速度基点法，联列4个特征点速度之间的矢量关系

(48)

其中

qj=M-Bj(j=1,2,3)

式中ω——动平台角速度

上标“^”表示矢量的反对称矩阵。

分别提取式(48)中3个矢量方程的第3行、第1行和第1行，构成一组新的独立方程

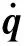
(49)

其中

式中 (·)k——矢量的第k个元素

综合式(17)、(44)～(47)、(49)，得到动平台角速度的解析解

(50)

值得一提的是，当矩阵Jω奇异时，式(50)不成立；此时，机构处于奇异位形，在下节中详细讨论。至此，解决了并联机构的速度正解问题。直接对速度正解中的v和ω求导，即得到加速度正解，这里不再赘述。

2.4 奇异曲面方程

由式(44)、(49)得到并联机构动平台速度与特征点速度之间的线性映射关系

(51)

其中

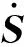
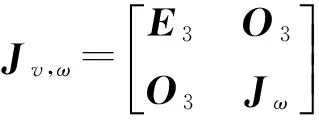
式中Jv,ω——正向雅可比矩阵

E3——三阶单位矩阵

O3——三阶零矩阵

由式(44)～(47)可得特征点速度与支链速度之间的线性映射关系

(52)

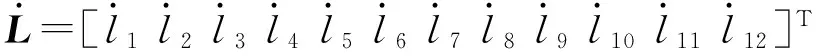
式中JL——逆向雅可比矩阵

由式(51)、(52)，得到并联机构动平台速度与支链速度之间的解析映射关系

(53)

当锁定动平台的输出时，式(53)转换为

(54)

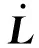
进一步地，结合矩阵理论，得到新型并联机构的第1类奇异曲面方程

(55)

特殊地，当所有支链均采用微幅驱动时，式(55)可以展开成

L2+2Ln+2n2=0

(56)

由于n、L均为正数，式(56)一定不成立，第1类奇异曲面方程无解，故机构不存在第1类奇异位形。

当锁定驱动支链的输入时，式(53)转换为

(57)

结合杆长协调方程可知，若rank(Jv，ω)<6，则v、ω的解不唯一，即存在非零解，机构学上表现为此时动平台出现了瞬时运动，这种现象对应于机构的第2类奇异[23]。

再结合矩阵理论，得到新型并联机构的第2类奇异曲面方程

det(Jω)=0

(58)

特殊地，当所有支链均采用微幅驱动时，式(58)可以展开成

3L2+Ln+2n2=0

(59)

同样，式(59)一定不成立，第2类奇异曲面方程无解，故机构也不存在第2类奇异位形。

机构的第3类奇异[23]是指同时满足1、2类奇异的情况，故新型并联机构奇异曲面方程是式(55)、(58)的组合。

综上所述，当动平台上的特征点坐标满足任意一组奇异曲面方程时，机构的运动状态不可控，对应的速度正解模型失效。

3 基于虚拟实验的算例验证

为验证正向运动学模型及其求解算法的正确性，在ADAMS虚拟实验平台上构建12-6台体型Stewart冗余并联机构的虚拟样机，如图5所示。其中，动平台的边长和支链的初始长度分别设定为30、25 mm。

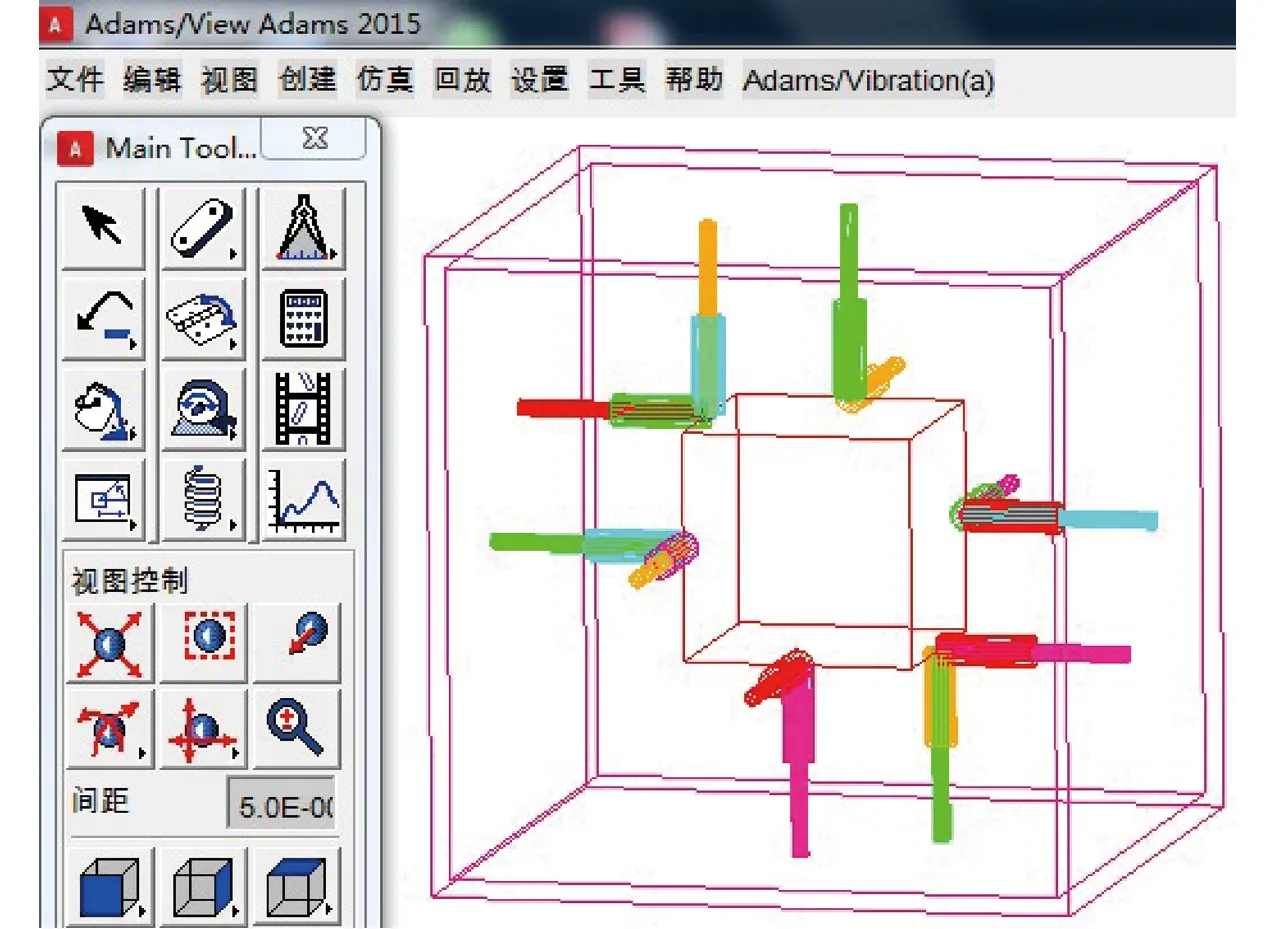
图5 12-6台体型Stewart冗余并联机构的虚拟样机Fig.5 Virtual prototype of general 12-6 Stewart redundant parallel mechanism

虚拟实验中，将动平台设定为刚体，另外，不考虑球面副、移动副的摩擦和间隙。在View模块下，对动平台同时施加线性、旋转驱动，驱动方程分别为

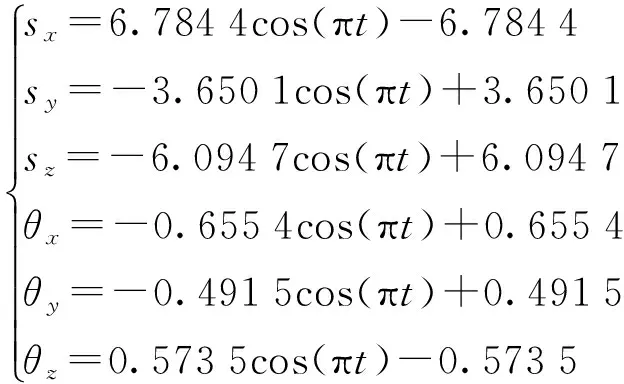
(60)

式中t——时间，s

sx、sy、sz——3个正交方向的线位移，mm

θx、θy、θz——3个正交方向的角位移，rad

将时间和步长分别设定为60、0.001 s，虚拟实验结束后，测量并导出12条杆长数据以及动平台上特征点的运动参数。将杆长数据及样机参数代入位姿正解模型中，计算6个独立未知量，并将其与测量值进行对比。经核查，所有采样节点处均未出现增根或失根的情况。列出2种典型构型下的特征项对比值，如表1所示。结果显示，位姿正解的计算值与测量值完全一致。

表1 位姿正解的精度验证Tab.1 Validation of precision of forwarddisplacement analysis mm

进一步地，将杆长数据代入速度正解模型中，并运用数值微分算法中的“三点公式”，计算动平台的线速度和角速度。同样地，将计算值与测量值进行对比，其综合误差[5]如图6所示。结果表明，两者基本吻合，且最大相对误差仅为0.08%，主要来源于数值微分中的截断误差。

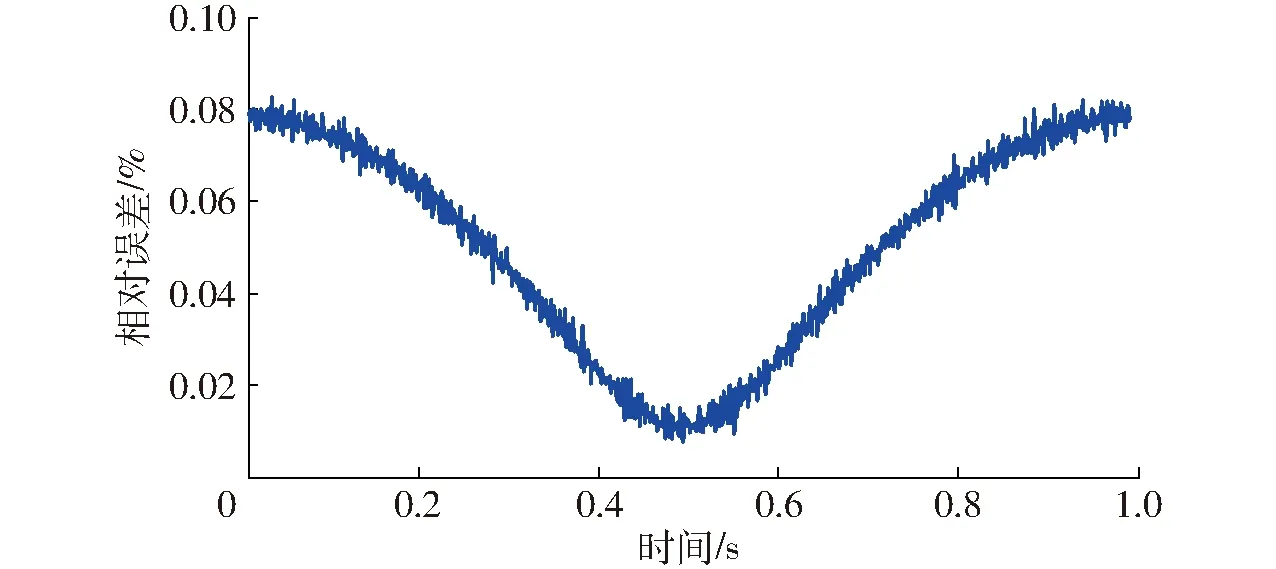
图6 速度正解的综合相对误差Fig.6 Composite relative error of forward velocities analysis

为验证正解算法的计算效率，参照文献[5]中的定义，运用Matlab中的“tic-toc”指令获得1 min内位姿正解、速度正解的效率指标值(解算时间与采样时间之比)，并将其与同一构型、同一参数的并联机构在ADAMS内核算法中的指标值作对比，如表2所示。其中，解算时间包括数据读取、计算、保存的时间。结果显示，本文的计算效率远远高于ADAMS内核，其指标值小于1，故满足实时性要求。

表2 运动学正解的效率验证Tab.2 Validation of efficiency of forward kinematics

4 结论

(1) 提出了一种变体的六自由度Stewart平台，构型冗余且对称。机构中含有6个HSOC支路，但不含三重复合铰链，故便于制造和装配；10个BKC的最大耦合度为1，故结构上表现为弱耦合。

(2)基于若干对同构关系，15个2次约束相容方程可以转换成只关于动平台上特征点坐标的1次多项式，实现了并联机构位姿正解的全解析化，结果唯一确定且无增根和失根。该方法同样适用于动平台上含3个以上二重复合球面副且耦合度小于2的台体型并联机构的正向运动学求解。

(3)以特征点的速度为中间量，运用基点法和微分法直接得到速度正解的全解析式，形式简洁、便于程式化。结果表明，动平台线速度的解一定唯一，角速度的解在机构的非奇异位形下也唯一。

(4)虚拟实验结果表明，位姿正解算法零误差，效率指标值为0.21；速度正解最大相对误差为0.08%，效率指标值为0.32。这表明，该类型并联机构及其运动学正解算法能够适用于实时反馈控制的场合。

1 STEWART D. A platform with six degrees of freedom [J]. Proceedings of the Institution of Mechanical Engineering, 1965, 180(15): 371-386.

2 WEN K, DU F Z, ZHANG X Z. Algorithm and experiments of six-dimensional force/torque dynamic measurements based on a Stewart platform [J]. Chinese Journal of Aeronautics, 2016, 29(6): 1840-1851.

3 徐刚，杨世模，龚雨兵. 大型光学望远镜副镜位姿精调机构的优化设计[J].光学 精密工程，2008，16(7): 1181-1189.

XU G，YANG S M，GONG Y B．Optimal design of pose and position fine tuning apparatus for secondary mirror in large optical telescope [J]. Optics and Precision Engineering, 2008, 16(7): 1181-1189. (in Chinese)

4 倪涛，朱厚文，张红彦，等. 基于手控器触觉共享控制的主从遥操作[J/OL].农业机械学报，2016，47(12): 367-373. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20161246&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2016.12.046.

NI T，ZHU H W，ZHANG H Y, et al. Master-slave teleoperation based on haptic device tactile shared control [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(12): 367-373. (in Chinese)

5 尤晶晶，李成刚，吴洪涛，等. 预紧式并联六维加速度传感器的解耦算法研究[J].仪器仪表学报，2017，38(5): 1216-1225.

YOU J J，LI C G，WU H T, et al. Research on the decoupling algorithm of pre-stressed parallel six-axis accelerometer [J]. Chinese Journal of Scientific Instrument, 2017, 38(5): 1216-1225. (in Chinese)

6 YANG X L, WU H T, LI Y, et al. Dynamic isotropic design and decentralized active control of a six-axis vibration isolator via Stewart platform [J]. Mechanism and Machine Theory, 2017,117: 244-252.

7 卢启鹏，李勇军，彭忠琦，等. 六杆并联机构运动学正解研究及其在同步辐射光束线中的应用[J].光学精密工程，2008，16(10):1874-1879.

LU Q P，LI Y J，PENG Z Q, et al. Forward kinematics of six-bar parallel mechanism and its applications in synchrotron radiation beam-line [J]. Optics and Precision Engineering, 2008, 16(10): 1874-1879. (in Chinese)

8 黄真，刘靖芳，李艳文. 论机构自由度——寻找了150年的自由度通用公式[M].北京：科学出版社，2011.

9 耿明超，赵铁石，王唱，等. 基于拟Newton法的并联机构位置正解[J].机械工程学报，2015，51(9): 28-36.

GENG M C，ZHAO T S，WANG C, et al. Direct position analysis of parallel mechanism based on quasi-Newton method [J]. Journal of Mechanical Engineering, 2015, 51(9): 28-36. (in Chinese)

10 ZHOU W Y, CHEN W Y, LIU H D, et al. A new forward kinematic algorithm for a general Stewart platform [J]. Mechanism and Machine Theory, 2015,87: 177-190.

11 YANG X L, WU H T, LI Y, et al. A dual quaternion solution to the forward kinematics of a class of six-DOF parallel robots with full or reductant actuation [J]. Mechanism and Machine Theory, 2017,107: 27-36.

12 黄昔光，廖启征，魏世民，等. 一般6-6型平台并联机构位置正解代数消元法[J].机械工程学报，2009，45(1): 56-61.

HUANG X G，LIAO Q Z，WEI S M, et al. Forward kinematics analysis of the general 6-6 platform parallel mechanism based on algebraic elimination [J]. Chinese Journal of Mechanical Engineering, 2009, 45(1): 56-61. (in Chinese)

13 程世利，吴洪涛，王超群，等. 基于正交补的6-3 Stewart并联机构运动学正解[J].中国机械工程，2011，22(5): 505-509.

CHENG S L，WU H T，WANG C Q, et al. Forward kinematics analysis of 6-3 Stewart parallel mechanisms based on orthogonal complement method [J]. China Mechanical Engineering, 2011, 22(5): 505-509. (in Chinese)

14 WEI F, WEI S M, ZHANG Y, et al. Algebraic solution for the forward displacement analysis of the general 6-6 Stewart mechanism [J]. Chinese Journal of Mechanical Engineering, 2016, 29(1): 56-62.

15 INNOCENTI C. Direct kinematics in analytical form of the 6-4 fully-parallel mechanism [J]. ASME Journal of Mechanical Design, 1995, 117(1): 89-95.

16 SU H J, LIAO Q Z, LIANG C G. Direct positional analysis for a kind of 5-5 platform in-parallel robotic mechanism [J]. Mechanism and Machine Theory, 1999,34: 285-301.

17 沈惠平，尹洪波，王振，等. 基于拓扑结构分析的求解6-SPS并联机构位置正解的研究[J].机械工程学报，2013，49(21): 70-80.

SHEN H P，YIN H B，WANG Z, et al. Research on forward position solutions for 6-SPS parallel mechanisms based on topology structure analysis [J]. Journal of Mechanical Engineering, 2013, 49(21): 70-80. (in Chinese)

18 尤晶晶，李成刚，吴洪涛. 基于四面体构型的冗余并联机构的运动学分析[J].中国机械工程，2013，24(8): 1097-1102.

YOU J J，LI C G，WU H T. Kinematics analysis of redundant parallel mechanism based on tetrahedral configuration [J]. China Mechanical Engineering, 2013, 24(8): 1097-1102. (in Chinese)

19 KIM J S, JEONG Y H, PARK J H. A geometric approach for forward kinematics analysis of a 3-SPS/S redundant motion manipulator with an extra sensor using conformal geometric algebra [J]. Meccanica, 2016, 51(10): 2289-2304.

20 YANG T L, LIU A X, SHEN H P, et al. On the correctness and strictness of the position and orientation characteristic equation for topological structure design of robot mechanisms [J]. Journal of Mechanisms and Robotics, 2013, 5(2):021009.

21 沈惠平，朱小蓉，尹洪波，等. 并联机构的结构降耦原理及其设计方法[J].机械工程学报，2016，52(23): 102-113.

SHEN H P，ZHU X R，YIN H B, et al. Principle and design method for structure coupling-reducing of parallel mechanisms [J]. Journal of Mechanical Engineering, 2016, 52(23): 102-113. (in Chinese)

22 尤晶晶，左飞尧，严飞，等. 台体型并联机构及其位置正解的求解方法:中国, 201610594784.4[P]. 2016-11-23.

23 GOSSELIN C, ANGELES J. Singularity analysis of closed-loop kinematic chain [J]. IEEE Transactions on Robotics and Automation, 1990, 6(3): 281-290.