基于微环境参数集的茎干水分变化规律与估算模型研究

高 超 赵 玥 赵燕东

(1.北京林业大学工学院, 北京 100083； 2.城乡生态环境北京实验室， 北京 100083)

引言

在植物生理水分调解过程中，茎流速率、蒸腾速率和茎干水分是衡量植物生理水分状况的重要参数，测量这些生理参数对研究植物生理水分的变化规律及特征具有重大意义。目前，市场上已有成熟的茎流速率和蒸腾速率传感器，但是不同类型的传感器由于检测原理不同导致测量结果差异较大，并且茎流速率和蒸腾速率传感器的生产成本较高,难以大规模应用于实际生产。因此，一些学者开始研究茎流速率、蒸腾速率与土壤温湿度、空气温湿度、光合有效辐射等微环境参数的关系，并基于微环境参数集建立相关数学模型去估算茎流速率和蒸腾速率[1-4]。植物导管束与韧皮周围的细胞组织具有水分储存与释放功能，茎干水分正是衡量这种局部水分交换的参数，也有相关学者对此展开研究[5-7]。综上，基于植物微环境参数集的模型可以很好地估算植物茎流速率和蒸腾速率，但是存在模型过于复杂且变量较多的缺点；相关学者提出了检测植物茎干水分的可靠方法，但是关于茎干水分与植物微环境参数集模型的研究并不深入，尚未提出估算植物茎干水分的具体模型。

本文以杨树为研究对象，分析茎干水分与植物微环境参数集的变化关系，提出一种基于植物微环境参数集的杨树茎干水分估算模型。

1 材料与方法

1.1 试验地点及概况

试验地点位于北京市共青林场，地理坐标为116°43′39.9792″E、 40°6′35.82″N,森林面积1 067 hm2,主要分布在潮白河两岸, 主要土壤类型为沙土，有机质含量低，一般在1%以下，仅在个别低洼地区腐殖质较厚,可达3%，土壤pH值在7～8之间。选取10株树势良好、茎干通直的杨树作为试验样本，并采用相同的栽培管理方式。试验时间为2016年，试验地点年均气温12.5℃，年降水量592 mm，年晴天数131 d。

1.2 参数测定

土壤温湿度会影响植物根系的吸水速率，空气温湿度和饱和水汽压差会影响植物叶片的蒸腾速率，光合有效辐射会影响植物叶片的光合速率，因此这6个参数均与植物的生理水分调节活动密切相关，并将其统称为微环境参数集。试验中需要直接测定的参数包括土壤温湿度、空气温湿度、光合有效辐射以及茎干水分，饱和水汽压差可由空气温湿度估算得出。试验中使用美国Decagon公司5TM型传感器(温度：-40～60℃，±1℃；湿度：0～100%，±2%)测量土壤温湿度，使用芬兰Vaisala公司的HMP50-L6型传感器(温度：-10～50℃，±0.25℃；湿度：0～100%，±2%)测量空气温湿度，使用美国Li-Cor公司的LI-190R型传感器(0～10 000 μmol/(m2·s)，±5%)测量光合有效辐射，使用北京林业大学的BD-IV型植物茎干水分传感器(0～60%，±1%)测量茎干体积含水率。土壤温湿度传感器安装于地下50 cm处，空气温湿度和光合有效辐射传感器安装于距地面30 m高的监测塔上，茎干水分传感器安装于距地面1.5 m高的杨树茎干上。

1.3 数据采集与处理

试验中采用自主设计基于AVR128的多通道数字采集器，以上所需的各种传感器均连接到采集器上。采集器每10 min采集一条数据，1 d总计采集144条数据，并采用6点均值滤波对数据进行预处理，即每天记录存储24条数据。

2 结果与分析

2.1 茎干水分与微环境参数集的相关性

以2016年8月份采集的数据为样本(N=744)，对其中4株杨树茎干水分与微环境参数集进行Pearson相关性分析，试验结果如表1所示。从表1可以看出，在6个微环境参数中，空气湿度、饱和水汽压差、光合有效辐射与杨树茎干水分的相关性较大，其中饱和水汽压差、光合有效辐射与茎干水分呈现负相关，而空气湿度与茎干水分呈现正相关。由于饱和水汽压差依据空气温湿度估算得出，且与植物蒸腾作用、光合作用等生理过程密切相关[8-10]，因此以下主要探讨茎干水分与饱和水汽压差、光合有效辐射的关系。

表1 杨树茎干水分与微环境参数集的相关性Tab.1 Correlations between poplar stem water content and micro-environment parameter set

2.2 茎干水分与饱和水汽压差的关系

图1给出了连续14 d杨树茎干水分和饱和水汽压差的变化规律，茎干水分呈现出单波峰波谷的日变化规律，饱和水汽压差呈现出单波峰的日变化规律，且茎干水分的日变化量与饱和水汽压差的日变化量正相关，茎干水分的日变化量低于2%表明茎干水分通常比较稳定，在土壤水分充足情况下，茎干水分并不作为植物生理活动的主要供水源，这也与植物生理需水主要通过根系吸收土壤水分的理论相吻合[11-12]。图2给出了8月3日当天茎干水分与饱和水汽压差的日变化关系，由图2a可以看出，茎干水分与饱和水汽压差呈现出斜椭圆的变化规律，且椭圆的长轴与X轴的正方向夹角大于90°，即表明茎干水分与饱和水汽压差呈现负相关性，箭头方向为下一时刻的观测值，顺时针的旋转方向表明当饱和水汽压差达到最大值时，茎干含水率并没有达到最小值，茎干含水率的最小值相对于饱和水汽压差的最大值存在滞后；从图2b则可以更清晰地看出，在08:00茎干含水率达到最大值，在13:00饱和水汽压差达到最大值A，但在15:00茎干含水率才达到最小值C,滞后时间TCA为2 h，这种变化趋势也符合植物生理水分的日变化规律：在清晨饱和水汽压差上升和日照增强的双重激励下植物叶片气孔逐渐张开，使得导管内的负压降低，从而对导管周围的细胞水产生较大的吸力，使得这些细胞开始失水，茎干含水率开始下降，当下午随着日照逐渐减弱，叶片气孔开始关闭，使得导管内的负压回升，周围细胞开始补水，茎干含水率开始上升, 但是由于细胞膜和细胞壁的隔离阻碍作用，使水分子的渗透过程变得缓慢，因此细胞的失/补水是一个缓慢进行的过程，也就导致茎干水分滞后于饱和水汽压差[13-16]。

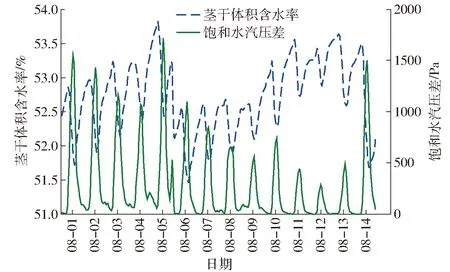
图1 茎干水分和饱和水汽压差的观测值Fig.1 Observed values for stem water content and vapor pressure deficit

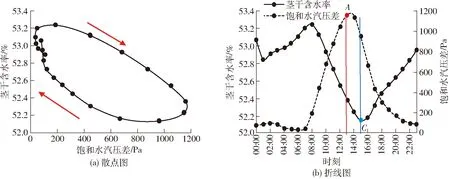
图2 茎干水分与饱和水汽压差的日变化关系Fig.2 Diurnal variation relationships between stem water content and vapor pressure deficit

2.3 茎干水分与光合有效辐射的关系

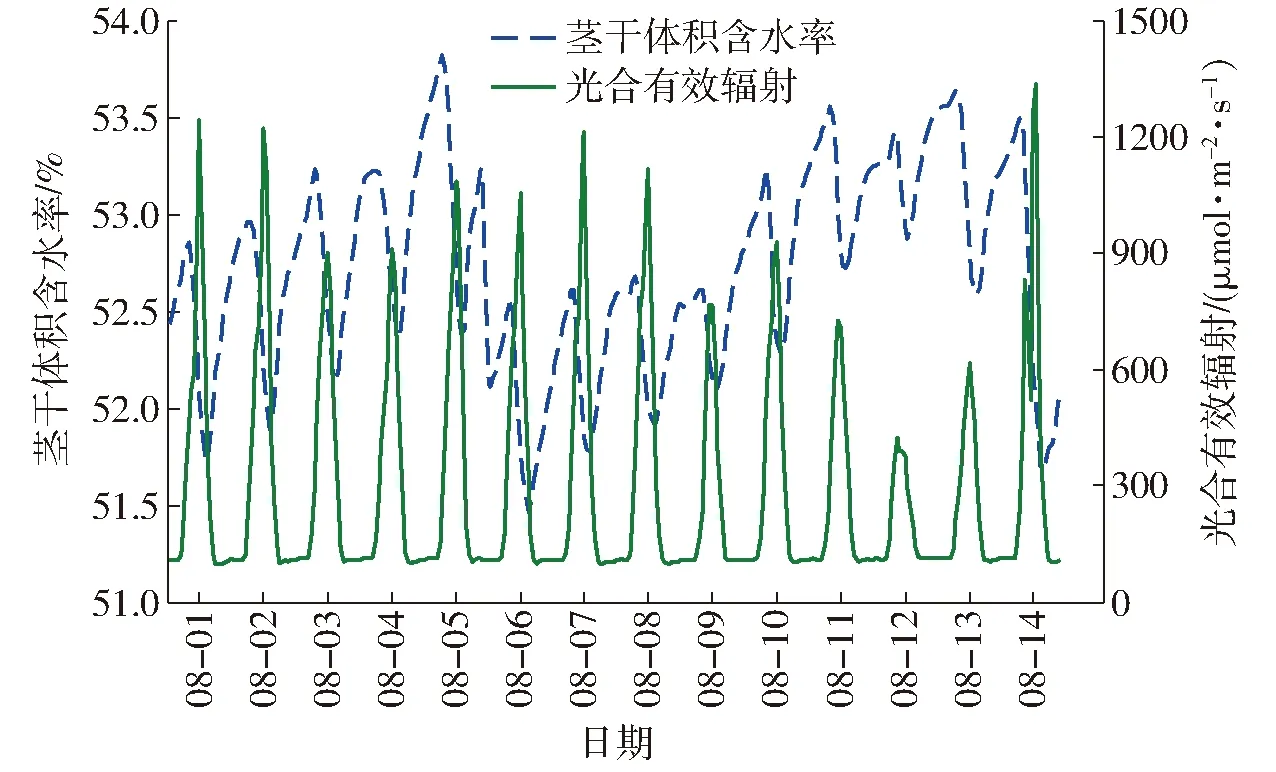
图3 杨树茎干水分和光合有效辐射的观测值Fig.3 Observed values for poplar stem water content and photosynthetic active radiation

图3给出了连续14 d杨树茎干水分和光合有效辐射的变化规律，光合有效辐射呈现出单波峰的日变化规律，且茎干水分的日变化量与光合有效辐射的日变化量正相关。图4给出了8月3日当天茎干水分与光合有效辐射的日变化关系，由图4a可以看出，茎干水分与光合有效辐射呈现出斜椭圆的变化规律，且椭圆的长轴与X轴的正方向夹角大于90°，即表明茎干水分与光合有效辐射呈现负相关性，对比图2a与图4a，可以发现前者斜椭圆的扁率大于后者，进一步表明茎干水分与光合有效辐射的相关性更弱，箭头的方向为下一时刻的观测值，顺时针的旋转方向表明当光合有效辐射达到最大值时，茎干含水率并没有达到最小值，茎干含水率的最小值相对于光合有效辐射的最大值存在滞后；从图4b则可以更清晰地看出，在08:00茎干含水率达到最大值，在12:00光合有效辐射达到最大值B，但在15:00茎干含水率才达到最小值C,滞后时间TCB为3 h，对比图2b与图4b,可以发现茎干水分滞后于饱和水汽压差的时间TCA小于茎干水分滞后于光合有效辐射的时间TCB，这是因为空气温湿度都受到日照的影响且存在滞后效应，因此饱和水汽压差也会滞后于光合有效辐射[17-18]。

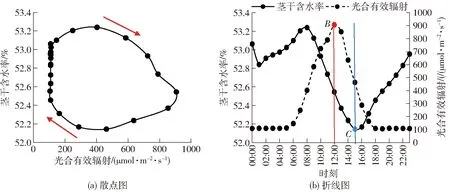
图4 茎干水分与光合有效辐射的日变化关系Fig.4 Diurnal variation relationships between stem water content and photosynthetic active radiation

3 模型描述与检验

3.1 主成分分析法选取的特征变量

微环境参数集之间不仅存在严重的共线性问题，而且有些参数对植物生理具有相反的作用。例如饱和水汽压差和光合有效辐射一般正相关，但是两者对植物叶片的气孔导度具有相反的作用。同样以2016年8月份采集的数据为样本(N=744)，对微环境参数集进行Pearson相关性分析，试验结果如表2所示。由表2可以看出，6个微环境参数之间存在共线性问题，尤其空气湿度、光合有效辐射、饱和水汽压差三者之间的相关系数大于0.8，表现为强相关。为了解决微环境参数集之间的共线性问题，本文采用主成分分析算法将微环境参数集投影变换到一系列主成分上，在保留绝大部分原始数据信息的同时，各主成分之间相互独立，并且达到数据降维的目的[19-21]。表3给出了微环境参数集3个主成分的特征值和贡献率，表4给出微环境参数集在这3个主成分上投影系数，由表3和表4可以看出，PC1对微环境参数集的贡献率达到98.89%，可以保证原始数据信息的相对完整性，并且光合有效辐射、饱和水汽压差在PC1上的投影系数较大，表明这两者对PC1起到主导作用。图5给出了8月3日当天茎干水分和PC1的日变化关系，从图5可以看出，茎干水分与PC1同样呈现出斜椭圆的变化规律，且椭圆的长轴与X轴的正方向夹角小于90°，即表明茎干水分与PC1呈现正相关性，箭头方向为下一时刻的观测值，逆时针的旋转方向表明茎干水分相对于PC1存在滞后。

3.2 模型描述

椭圆的标准方程经过平移和旋转变换之后可以得到斜椭圆的标准方程，其数学解析式为

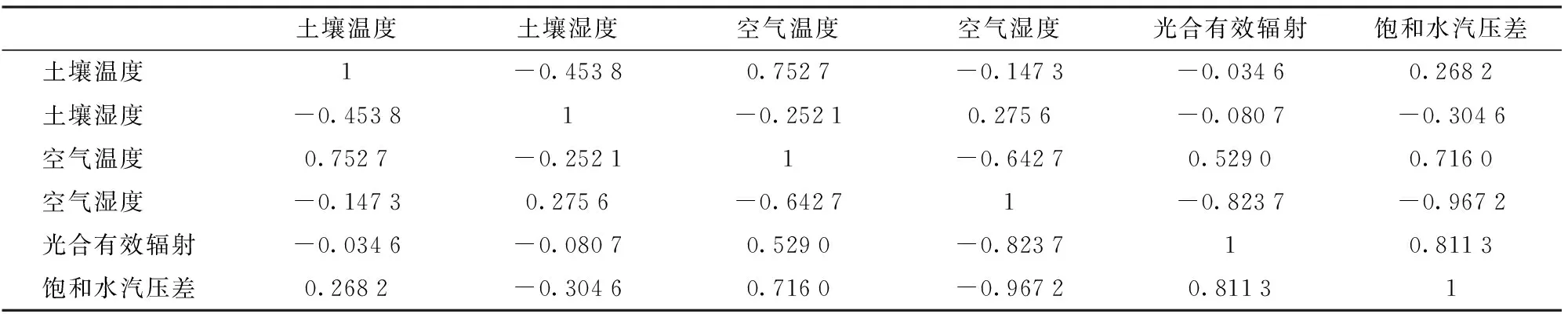
表2 微环境参数集之间的相关系数Tab.2 Correlations between micro-environment parameter set

表3 不同主成分下的特征值和贡献率Tab.3 Eigenvalues and contribution rates using different numbers of principal component

表4 不同主成分下的投影系数Tab.4 Projection coefficients using different numbers of principal component

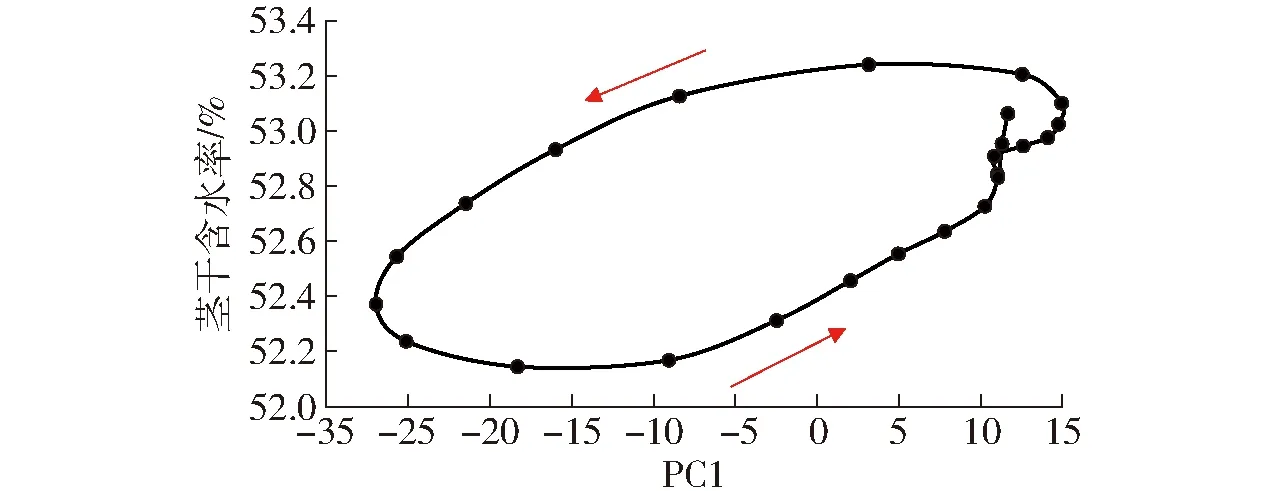
图5 茎干水分与PC1的日变化关系Fig.5 Diurnal variation relationship between stem water content and PC1

(1)

式中A——斜椭圆的长半轴

B——斜椭圆的短半轴

S——斜椭圆中心点的横坐标

T——斜椭圆中心点的纵坐标

θ——斜椭圆长轴按顺时针旋转与X轴正方向的夹角，(°)(θ<90°)

X——微环境参数集的最大主成分PC1

Y——茎干含水率，%

图6 茎干水分与PC1的斜椭圆模型Fig.6 Oblique ellipse models between stem water content and PC1

该模型中A、B、S、T、θ均为预估参数,可由数值稳定的直接最小二乘法估算得出[22-25]，其中S表示日平均最大主成分，T表示日平均茎干含水率。tanθ表示斜椭圆长轴的斜率，可定义tanθ为茎干含水率相对于微环境参数集最大主成分的灵敏度，扁率e=(A-B)/A表示斜椭圆的扁平程度，可定义e为茎干含水率相对于微环境参数集最大主成分的相关度。X为唯一的输入变量，Y为输出变量，因此在估算出预估参数之后，即可得到关于茎干含水率Y的一元二次方程，再结合(X,Y)按时间序列随斜椭圆逆时针的变化规律，便可求解唯一的茎干含水率Y。

3.3 模型检验

以2016年8月份采集的数据为样本,选取其中微环境状况极为相近的6个晴天作为模型的检验集。图6给出了这6 d两株杨树的茎干水分与微环境参数集最大主成分PC1的斜椭圆模型，表5给出了斜椭圆模型的预估参数，表6给出了斜椭圆模型的性能指标。从表6可以看出，杨树1斜椭圆模型tanθ值接近杨树2的2倍，表明杨树1对微环境参数的变化更加敏感，而两者的扁率e近乎相等，进一步表明杨树1和杨树2所处的微环境状况相同。与此同时，这两个斜椭圆模型的平均误差均小于0.05%，均方根误差均小于0.06%，决定系数均大于0.94，表明在微环境状况相近的情况下，该模型能够较好地依据微环境参数集估算出实时的茎干含水率，但是2个模型的预估参数存在一定差异，表明在微环境状况相同的情况下，茎干水分还与其他参数相关。由于植株胸径、冠幅以及叶面积指数等形态指标与蒸腾速率、茎流速率密切相关[26-28]，因此茎干水分与植株形态指标也存在一定关联，这也在试验中得到了验证。对比2个模型的预估参数T，可以发现杨树1的日平均茎干含水率小于杨树2，这是因为杨树1的胸径比杨树2大4 cm，这种现象也符合杨树的生理结构变化规律：对于成年杨树而言，随着胸径的增大，边材体积比较稳定，而心材体积逐渐增大，茎干的总体含水量增加，但是增速小于茎干体积的增速，因此茎干体积含水率呈减小趋势。

不同季节具有不同的气候特征，同一季节晴天和阴天的气象环境也相差较大，因此针对不同季节和气象环境需要分别建立典型的茎干水分估算模型。

表5 斜椭圆模型的预估参数Tab.5 Estimated parameters of oblique ellipse models

表6 斜椭圆模型的性能指标Tab.6 Performance indexes of oblique ellipse models

4 结论

(1)杨树茎干水分与微环境参数集密切相关，尤其与饱和水汽压差、光合有效辐射具有较强的负相关性，茎干水分呈现出单波峰波谷的日变化规律，且日变化量不超过2%，茎干水分的最小值分别滞后于饱和水汽压差的最大值和光合有效辐射的最大值，且滞后于前者的程度小于后者。

(2)采用主成分分析法选取微环境参数集的最大主成分PC1作为特征变量，解决了微环境参数集之间的共线性问题，并在保留98.89%的原始数据信息的同时，达到了数据降维的目的，从而降低了模型的复杂度。

(3)以PC1作为输入变量，茎干水分作为输出变量，基于两者的周期性变化规律建立了茎干水分与PC1的斜椭圆模型。在微环境状况相近的情况下，该模型的平均误差小于0.05%，均方根误差小于0.06%，决定系数大于0.94，能够较好地依据微环境参数集估算出实时的茎干含水率。但是由于植株个体存在形态指标上的差异，不同植株茎干水分与PC1的斜椭圆模型的预估参数也会存在差异，针对不同季节和气象环境需要分别建立茎干水分的估算模型。

1 贾文杰,马璐琳,丁鲲,等. 百合生长期茎流特征及其与环境因子的关系[J]. 西北植物学报,2012,32(12):2498-2505.

JIA Wenjie, MA Lulin, DING Kun, et al. Characters of sap flow of lilium and its relations with environment factors[J]. Acta Botanica Boreali-Occidentalia Sinica, 2012,32(12):2498-2505.(in Chinese)

2 O’BRIEN J J, OBERBAUER S F, CLARK D B. Whole tree xylem sap flow responses to multiple environmental variables in a wet tropical forest[J]. Plant, Cell & Environment, 2004, 27(5): 551-567.

3 张中典,李建明,利继东,等. 温室番茄营养生长期叶片蒸腾速率的模拟模型研究[J]. 上海交通大学学报:农业科学版,2015,33(5):40-47.

ZHANG Zhongdian, LI Jianming, LI Jidong, et al. Study on the simulation model for leaves transpiration rate of greenhouse tomato in its vegetative growth period[J]. Journal of Shanghai Jiaotong University:Agricultural Science,2015,33(5):40-47.(in Chinese)

4 BOULARD T, WANG S. Greenhouse crop transpiration simulation from external climate conditions[J]. Agricultural and Forest Meteorology, 2000, 100(1): 25-34.

5 赵燕东,高超,张新,等. 基于驻波率原理的植物茎体水分无损检测方法研究[J/OL]. 农业机械学报,2016,47(1):310-316. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160142&flag=1.DOI:10.6041/j.issn.1000-1298.2016.01.042.

ZHAO Yandong, GAO Chao, ZHANG Xin, et al. Non-destructive measurement of plant stem water content based on standing wave ratio[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(1):310-316.(in Chinese)

6 周海洋,孙宇瑞, SCHULZE Lammers P,等. 基于内边缘场电容效应的树干/枝水分传感器研究[J/OL]. 农业机械学报,2016,47(1):317-323. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160143&flag=1.DOI:10.6041/j.issn.1000-1298.2016.01.043.

ZHOU Haiyang, SUN Yurui, SCHULZE Lammers P, et al. Inner fringing-filed capacitance sensor for measurement of stem water content[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(1):317-323.(in Chinese)

7 ZHOU H, SUN Y, TYREE M T, et al. An improved sensor for precision detection of in situ stem water content using a frequency domain fringing capacitor[J]. New Phytologist, 2015, 206(1): 471-481.

8 RAWSON H M, BEGG J E, WOODWARD R G. The effect of atmospheric humidity on photosynthesis, transpiration and water use efficiency of leaves of several plant species[J]. Planta, 1977, 134(1): 5-10.

10 SHIRKE P A, PATHRE U V. Influence of leaf-to-air vapour pressure deficit (VPD) on the biochemistry and physiology of photosynthesis inProsopisjuliflora[J]. Journal of Experimental Botany, 2004, 55(405): 2111-2120.

11 梁宗锁,康绍忠. 作物水分代谢及其调节[J]. 西北植物学报,1996,16(6):73-78.

LIANG Zongsuo, KANG Shaozhong. Water metabolism and regulation of crop[J]. Acta Botanica Boreali-Occidentalia Sinica, 1996,16(6):73-78.(in Chinese)

12 KOZLOWSKI T T. Water metabolism in plants[J]. Soil Science, 1964, 98(2): 143.

13 KIM Y X, STEUDLE E. Light and turgor affect the water permeability (aquaporins) of parenchyma cells in the midrib of leaves ofZeamays[J]. Journal of Experimental Botany, 2007, 58(15-16): 4119-4129.

14 KIM Y X, STEUDLE E. Gating of aquaporins by light and reactive oxygen species in leaf parenchyma cells of the midrib ofZeamays[J]. Journal of Experimental Botany, 2009, 60(2): 547-556.

15 李吉跃,高丽洪.内聚力-张力学说的新证据[J].北京林业大学学报,2002,24(4):135-138.

LI Jiyue, GAO Lihong. New evidence for cohesion-tension theory[J]. Journal of Beijing Forestry University, 2002,24(4):135-138.(in Chinese)

16 POCKMAN W T, SPERRY J S, LEARY J W O. Sustained and significant negative water pressure in xylem[J]. Nature, 1995, 378(6558): 715-716.

17 BRISTOW K L, CAMPBELL G S. On the relationship between incoming solar radiation and daily maximum and minimum temperature[J]. Agricultural and Forest Meteorology, 1984, 31(2): 159-166.

18 ABRAHA M G, SAVAGE M J. Comparison of estimates of daily solar radiation from air temperature range for application in crop simulations[J]. Agricultural and Forest Meteorology, 2008, 148(3): 401-416.

19 BALLABIO D. A Matlab toolbox for principal component analysis and unsupervised exploration of data structure[J]. Chemometrics and Intelligent Laboratory Systems, 2015, 149(12): 1-9.

20 ABDI H, WILLIAMS L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 2(4): 433-459.

21 BRO R, SMILDE A K. Principal component analysis[J]. Analytical Methods, 2014, 6(9): 2812-2831.

22 MULLETI S, SEELAMANTULA C S. Ellipse fitting using the finite rate of innovation sampling principle[J]. IEEE Transactions on Image Processing, 2016, 25(3): 1451-1464.

23 PANAGIOTAKIS C, ARGYROS A. Parameter-free modelling of 2D shapes with ellipses[J]. Pattern Recognition, 2016, 53(5): 259-275.

24 MAINI E S. Enhanced direct least square fitting of ellipses[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2006, 20(6): 939-953.

25 O’LEARY P, ZSOMBOR-MURRAY P. Direct and specific least-square fitting of hyperbol and ellipses[J]. Journal of Electronic Imaging, 2004, 13(3): 492-503.

26 AYYOUB A, ER-RAKI S, KHABBA S, et al. A simple and alternative approach based on reference evapotranspiration and leaf area index for estimating tree transpiration in semi-arid regions[J]. Agricultural Water Management, 2017, 188(7): 61-68.

27 CHEN Y J, BONGERS F, TOMLINSON K, et al. Time lags between crown and basal sap flows in tropical lianas and co-occurring trees[J]. Tree Physiology, 2016, 36(6): 736-747.

28 MOTZER T, MUNZ N, KUPPERS M, et al. Stomatal conductance, transpiration and sap flow of tropical montane rain forest trees in the southern Ecuadorian Andes[J].Tree Physiology, 2005, 25(10): 1283-1293.