基于Matlab常微分方程数值解的分析与比较

马泽涛

[摘 要]本文借助Matlab常微分方程求解工具箱，从时间与精度两个方面对刚性和非刚性方程的数值求解进行分析与比较，进而对常微分方程的求解给出一般的建议。

[关键词]常微分方程；时间；精度； 刚性方程；非刚性方程

[中图分类号] G642 [文献标识码] A [文章编号] 2095-3437（2017）12-0050-03

常微分方程现代数学的一个重要组成部分，是研究自然科学、社会科学中事物运动变化规律最基本的数学理论和方法，是各种应用型学科和数学理论研究都不可缺少的工具。但绝大多数常微分方程都不能求得解析解。因此，要分析与比较不同数值解法[1][2][3][4]，面对用户不同层次的要求，找到最优解法是急需解决的问题。根据常微分方程理论，一阶常微分方程初值问题

上述的方法在求解刚性方程和非刚性方程时，有各自的优点，又都存在着一定的局限性。例如：一般情况下，若采用函数ode45求解刚性方程时，结果会很糟糕甚至是死机。即使求得了相应的数值解，所得的结果也会和精确解相差较大。因此，在将常微分方程分为刚性方程和非刚性方程后，针对它们各自的特殊性，从求得数值解所用的时间和精度这两个方面，来对比总结出较好的方法。

一、基于时间的比较

上述ode系列函数所基于的数学思想方法不同，主要是步长取法上的差异，而步长的选取对数值计算有很大的影响。步长选取较大虽然会减少方程求解在计算机中的运行时间，但保证不了求解精度；步长选取过小，虽然保证了求解的精度，却会引起计算机中的多次舍入误差的积累及运行时间的增加。因此，产生了变步长的算法，它能很好地平衡这两方面。然而，有的用户仅需要了解方程解的大概分布情况，对精度的要求不太高，因此针对时间方面，我们做了如下的比较。

对于刚性方程（2）来说，首先，基于ode15s，ode23s，ode23t和ode23tb这四个函数都只能求得低精度的数值解情况下，又从上表的各函数运行所需时间可以看出，函数ode15s和ode23t所需时间明显少于ode23tb和ode23s，并且函数ode23tb又明显优于ode23s。

其次，在这4个函数都是隐格式情况下，函数ode15s采用的是多步长法，而ode23s，ode23t和ode23tb采用的都是单步长法。从上表可以看出，多步长法在运行时间方面具有较大的优势。在单步法中，函数ode23t的运行时间又少于其他函数。因此，在求解这类刚性方程且求解精度相差不大的四种函数中，函数ode15s是最佳的求解办法，ode23t次之。

而对于非刚性方程（3），从上表中可以看到，函数ode113运行时间最少，ode23次之，ode45最多。

这是因为，这三个函数中，函数ode45与ode23采用的都是变步长的单步法，而ode113采用的是多步法。变步长法即在解变化大的地方采用小步长，解变化小的地方采用大步长。但许多理论和研究都表明，在解变化小的地方仍然不能采用大步长，否则会导致误差的急剧增加。于是，為了保证函数ode45和ode23的求解精度，并没有在解变化小的地方采用大步长，从而导致了其运算次数的增加。相应的，和多步法的函数ode113相比，运算时间上也不占优势。因此，求解非刚性方程时，函数ode113运行时间最少，是最佳的求解办法，ode23次之，ode45最慢。

二、基于精度的比较

其次，单纯地要求运行时间少并不利于更好的研究解的性质。在精度方面，我们可以发现，多步法提出了一种新的逼近，但是许多必需的计算将被求解过程中已经算得的值的插值所代替。且采用多步长算法的函数的求解精度往往比采用单步长算法的函数的求解精度要高。于是，在不考虑时间因素的情况下，作了如下比较。

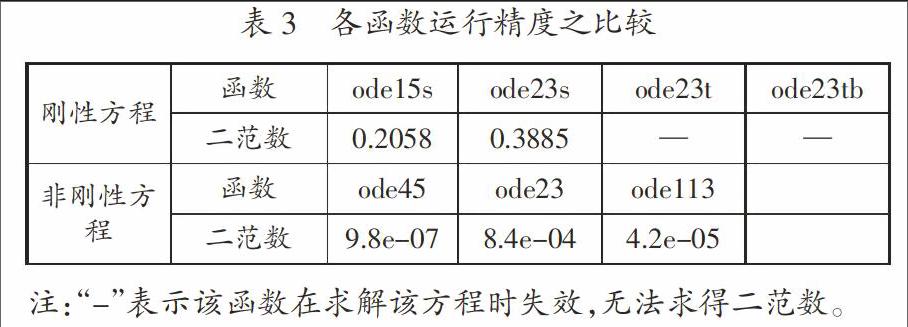
对于刚性方程（4）来说，首先，可以知道函数ode23t和ode23tb在求解该方程时失效。因此，在求解刚性方程时，在四个求解刚性方程的函数中，函数ode23t和ode23tb不是首要选择。

再讨论函数ode15s和ode23s的精度。函数ode15s采用的是多步法，而ode23s采用的是单步法。多步法利用前面若干个节点得到下一点的近似值，相比只利用了前一个节点得到下一点的单步法得到的数据更具说服力与科学性。再比较二者的二范数，由于0.2058<0.3885，所以函数ode15s是求解这个微分方程的最佳方法，ode23s次之。

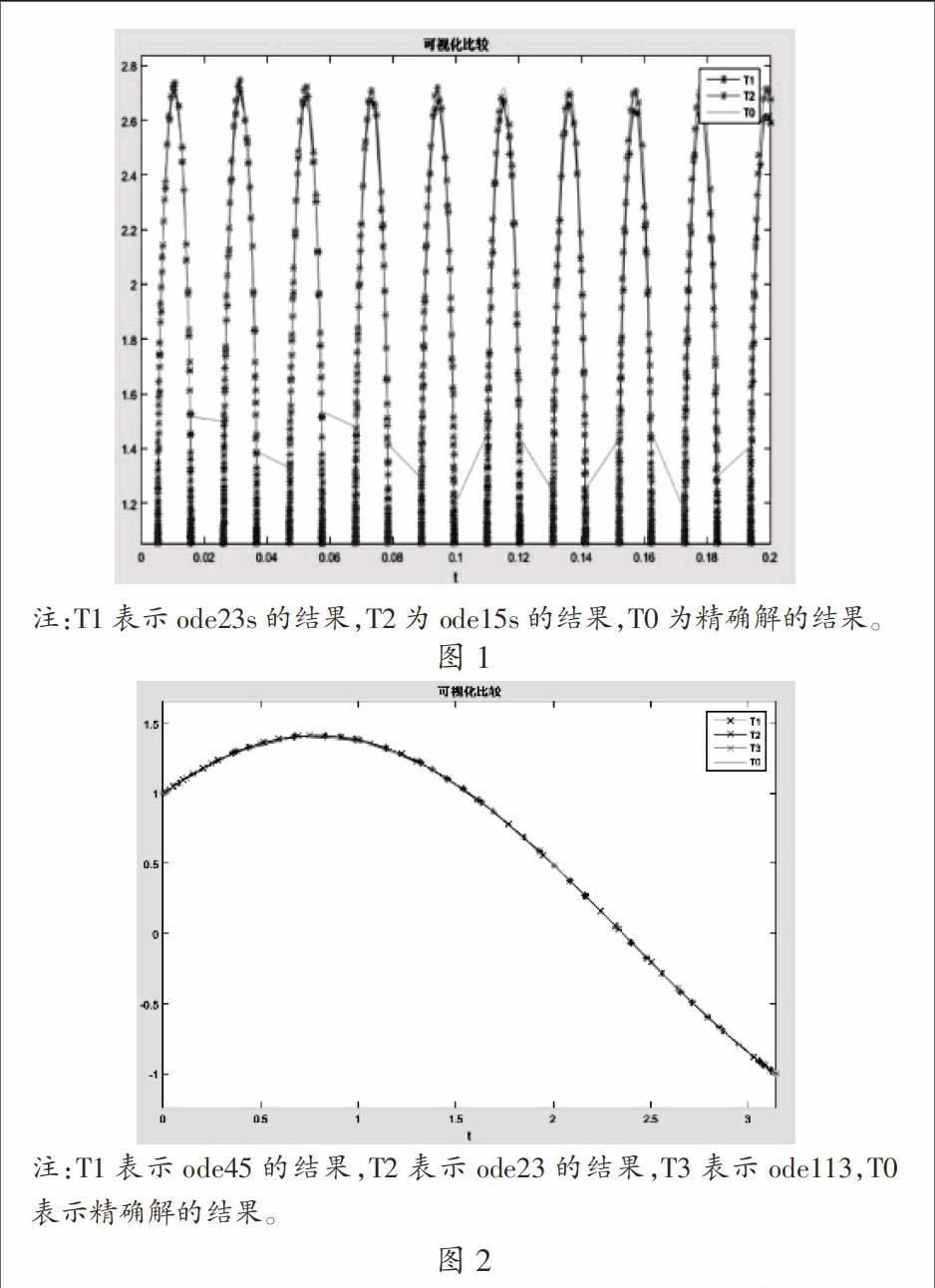
而对于非刚性方程（5），首先可以发现这三个函数都能求得相应的二范数，故函数ode45，ode23，ode113都可用来求解此方程。其次，根据二范数的比较可知，函数ode45所求精度最高，ode113其次，ode23最差。

由于这三个函数都是显格式，我们进行其他算法上的综合比较。函数ode45和ode23都是单步法，其中函数ode45采用的是Runge-Kutta法的四、五阶算法，函数ode23是Runge-Kutta法的二、三阶算法，函数ode45阶数更高，则所求精度也越高；而函数ode113是多步法，故函数ode113优于ode23。然而，函数ode113是变精度变阶次的算法，在这里它所求阶次比函数ode45要低，故此例中函数ode45更优。这从另外一个方面也可以说明，可能会有函数ode113所求精度比ode45高的情况出现。

三、基于实际应用的分析

应用1：导弹追踪问题

从上表的运行时间上可以看出，函数ode45，ode23与ode113所需时间和我们之前所得结论相吻合。然而，从二范数的比较中可以发现函数ode23所求精度高于函数ode113，与之前所得结果有一点出入，这是由于函数ode113是变精度变阶次的算法，在求解该方程时，比Runge-Kutta法的二、三阶算法所求精度更低。因此，在面对非刚性方程时，在精度方面要对函数ode113格外注意，在条件允许的情况下，可以尝试其他函数取更优法。endprint

应用2：化学反应问题

从上表的所需时间看出，这四个函数均与方程（2）所得结论相吻合。然而，在精度方面由于方程（4）我们所选方程的特殊性，函数ode23t和ode23tb不能用于求解该方程，而在此化学反应中，这四个函数都可用于求解此方程，并且函数ode15s所求精度最高，其次分别是函数ode23t，ode23s及ode23tb。究其原因，也是由于函数ode15s采用的是多步长算法，而函数ode23t，ode23s及ode23tb采用的是单步长算法。所以，在选用函数ode23t和ode23tb时，也应该格外注意其使用其局限性，实际上这就需要我们关注方程的求解区间。

四、结语

通过以上几个例子及应用，我们可以发现：在已知方程刚性与否的情况下，在运用Matlab中ode系列函数求常微分方程数值解时，对于大多数刚性方程，若只要求运行时间少但对精度要求不高，多步法与单步法相比占有很大的优势，因此函数ode15s是首选，ode23t次之；而在对精度有一定要求但不考虑时间的情况下，多步法同样优于单步法，从而函数ode15s是首选，ode23s次之。对于一般的非刚性方程，若只考虑时间，采用变精度变阶次的Adams？鄄Bashforth？鄄Moulton校正法的函数ode113是首选；若只考虑精度，采用自动变步长的R？鄄K方法的函数ode45是首选，ode113次之。

因此，综合考虑求解精度和运行时间这两方面，对于非刚性方程来说，函数ode113在某些方程中都是最佳选择，其次考虑尝试用函数ode45；而对于刚性方程来说，函数ode15s是最佳选择。当然，考虑到还有众多常微分方程在未能准确判断其刚性与否的情况下，可以优先尝试函数ode45，而ode45失效时再尝试ode15s。

[ 参 考 文 献 ]

[1] 李庆扬，王能超，易大义.数值分析（第五版）[M].北京：清华大学出版社，2008.

[2] 魏明强.一阶常微分方程数值解中四种算法的实例比较[J].中国传媒大学报（自然科学版），2016（2）：41-44.

[3] 孙美玲.常微分方程数值解法的Matlab计算与可视比较[J].高教学刊，2016（19）：60-61.

[4] 胡庆婉.常微分方程初值问题的数值求解及MATLAB实现[J].SCIENCE & TECHNOLOGY INFORMATION，2012（7）：34-35.

[5] 王高雄，等.常微分方程[M].北京：高等教育出版社，2006（7）：120-121.

[6] Richard L.Burden，J.Douglas Faires.Numberical Analysis[J].Higher Education Press Thomson Learning，Inc，2001（3）：348-353.

[7] 宋叶志，等.MATLAB数值分析与应用[M].北京：机械工业出版社，2014（2）：384-393.

[8] 张晓.Matlab微分方程高效解法：譜方法原理与实现[M].北京：机械工业出版社，2015（9）：9-12.

[9] 袁东锦.数值分析=Numberical Analysis[M].南京：东南大学出版社，2005（8）：158-166.

[10] 李庆扬，等.数值计算原理[M].北京：清华大学出版社，2000（9）：372-376.

[责任编辑：林志恒]endprint