单锚点与多锚点抗滑桩抗震性能数值计算研究

陈晋波　吴红刚　艾挥

摘要：锚索抗滑桩作为一种常用的高边坡支挡结构，目前对单锚点与多锚点锚索抗滑桩在高烈震区的抗震性能研究较少。为了进一步分析单锚点与多锚点的抗震表现，本文以ABQUSE软件分别建立单锚点与多锚点加固边坡的三维数值模型。研究了不同向加载工况下，不同动峰值的EL-Centro波加速度作用下，边坡的位移变形规律以及桩的山侧动土压力、弯矩、剪力分布规律。并得出以下结论：①从坡体的位移变形来看，输入相同的EL-Centro波动峰值加速度，X加载时的坡体水平位移比z向加载时位移变化明显，不利于坡面稳定，且XZ双向加载时的坡体位移比单向加载要大。②从锚索抗滑桩土压力分布曲线来看：多锚点滑面处动土压力相对较小，抗震性能较好。③相同动峰值加速度作用下，多锚点锚索抗滑桩加固的坡体产生的位移相对较小，有利于控制坡体的变形，且多锚点锚索抗滑桩桩身弯矩、剪力值相对较小，支挡效果较好。

关键词：锚索抗滑桩；地震；数值模拟

中图分类号：TU473.1 文献标识码：A 文章编号：1006-431l（2017）30-0107-06

0引言

预应力锚索抗滑桩是在抗滑桩的基础上发展起来的。由于在工程中的大量应用，对于预应力锚索抗滑桩的研究，相比国外对横向桩的研究，我国在这一方面处于世界的前列。目前，国内外对于预应力锚索抗滑桩的研究主要集中在静力方面：谢庆华通过对预应力锚索抗滑桩治理广西某二级公路滑坡进行了现场测试，研究了桩身应力与桩深的关系。曾云华等通过室内预应力锚索抗滑桩模型试验，分析了滑坡推力对抗滑桩的作用分布形式，认为桩前滑体抗力可作为安全储备来考虑。张玉芳等通过深圳市黄贝岭滑坡治理工程的预应力锚索桩的现场监测结果，分析了锚索拉力随时间的变化的关系。对于预应力锚索抗滑桩的加固机理以及加固效果方面的研究，国内外基本上还处于起步研究阶段，公开报道的成果较少。总体而言，相对于其工程应用，锚索抗滑桩的理论研究明显滞后。至于单锚点与多锚点抗滑桩的动力特性方面的研究，目前相关报道极少。仅有艾挥和吴红刚等H通过振动台对比试验初步对单锚点与多锚点锚索抗滑桩加固边坡的变形与受力规律进行了初步探讨。大量统计结果表明7度及以上烈度区发生地震都会诱发滑坡发生，并且随着烈度的增高，产生滑坡的概率也相应增大。可见，有必要通过数值模拟对高烈震区单锚点与多锚点锚索抗滑桩抗震性能进行分析研究。

1基本假定与计算模型

1.1基本假定本次计算模型未考略锚索对土体影Ⅱ向，并且在模型计算时，设定锚索只产生弹性阶段变形，且变形量不超过锚索自由段长度的3%：考虑到土体本构关系及其变形对应力的影响，计算模型计算采用Mohr-Coulonb模型。

1.2计算模型为了更好地反映在地震作用下，单锚点与多锚点锚索的动力特性，采用ABQUSE软件分别建立单锚点与多锚点锚索抗滑桩加固边坡的计算模型，其几何尺寸的长、宽、高分为3.0m×1.5m×1.14m，桩长70cm，其中悬臂段35cm，锚固段35cm。

为了提高计算结果的精度，将几何模型进行划分为规则体连接。计算模型如图1所示。模型计算时，采用EL-Centro波进行模型计算，选用的EL-Centro波加速度时程曲线如图2所示。

模型材料基本力学参数见表1、表2。模型计算时，单锚点锚索抗滑桩单根锚索拉力设为24N，多锚点锚索抗滑桩设置锚索2根，拉力各为12N。

2数值模型结果分析

本节主要分析地震烈度不超过Ⅸ时，单锚点与多锚点锚索抗滑桩加固边坡的位移变形规律和动土压力分布形式。并以X向加载为例，分析了单锚点与多锚点锚索抗滑桩弯矩、剪力随输入EL-Centro波动峰值加速度的变化分布规律。

2.1单锚点锚索抗滑桩加固边坡位移变形图

图3为在0.1g的Z向EL-Centro波作用下，单锚点锚索抗滑桩加固边坡的位移变形图。从图（a）中可以看出，模型后缘浅表层土体在Z向发生的位移值最大，值为1.020E-03m，坡體后缘率先出现微小裂缝。随着模型高度的降低，土体的位移依次减小，表明振动作用下，高程效应明显。从图（b）中可以看出，在0.1g的Z向EL-Centro波作用下，桩后土体在滑面及以下部位位移较大，最大值为8.041E-05m。从坡面水平位移变化来看，从顶端到底部，水平位移依次增大。

图4为在0.1g的X向EL-Centro波作用下，单锚点锚索抗滑桩加固边坡的位移变形图。从图（a）中可以看出，模型后缘浅表层土体在Z向发生的位移值最大，值为4.863E-04m振动作用下，高程效应明显。从图（b）中可以看出，在0.1g的x向EL-Centro波作用下，桩后土体在滑面处及以下部位位移较大，最大值为6.381E-04m，水平位移依次增大。

图5为在0.1g的XZ向EL-Centro波作用下，单锚点锚索抗滑桩加固边坡的位移变形图。从图（a）中可以看出，模型后缘浅表层土体在z向发生的位移值最大，值为1.091E-03m。随着模型高度的降低，土体的位移依次减小，表明振动作用下，高程效应明显。从图（b）中可以看出，在0.1g的XZ向EL-Centro波作用下，桩后土体在滑面处及以下位移较大，最大值为6.384E-04m。从坡面水平位移变化来看，从顶端到底部，水平位移依次增大，且比单向加载时位移要大。

2.2多锚点锚索抗滑桩加固边坡位移变形图

图6为在0.1g的Z向EL-Centro波作用下，多锚点锚索抗滑桩加固边坡的位移变形图。从图（a）中可以看出，模型后缘浅表层土体在Z向发生的位移值最大，值为1.020E-03m。随着模型高度的降低，土体的位移依次减小，表明振动作用下，高程效应明显。从图（b）中可以看出，在0.1g的X向EL-Centro波作用下，桩后土体在滑面处及以下位移较大，最大值为7.352E-05m。从坡面水平位移变化来看，从顶端到底部，水平位移依次增大。endprint

图7为在0.1g的x向EL-Centro波作用下，多锚点锚索抗滑桩加固边坡的位移变形图。从图（a）中可以看出，模型后缘浅表层土体在z向发生的位移值最大。值为0.487E-04m。随着模型高度的降低，土体的位移依次减小，表明振动作用下，高程效应明显。从图（b）中可以看出，在0.1g的X向EL-Centro波作用下，桩后土体在滑面处及以下位移较大，最大值为6.363E-04m。从坡面水平位移变化来看，从顶端到底部，水平位移依次增大。

图8为在0.1g的XZ向EL-Centro波作用下，多锚点锚索抗滑桩加固边坡的位移变形图。从图（a）中可以看出，模型后缘浅表层土体在z向发生的位移值最大，值为1.092e-03m。随着模型高度的降低，土体的位移依次减小，高程效应明显。从图（b）中可以看出，在0.1g的XZ向EL-Centro波作用下，桩后土体在滑面处及以下部位位移较大，最大值为6.365E-04m。从坡面水平位移变化来看，从顶端到底部，水平位移依次增大。

2.3动力压力计算结果分析

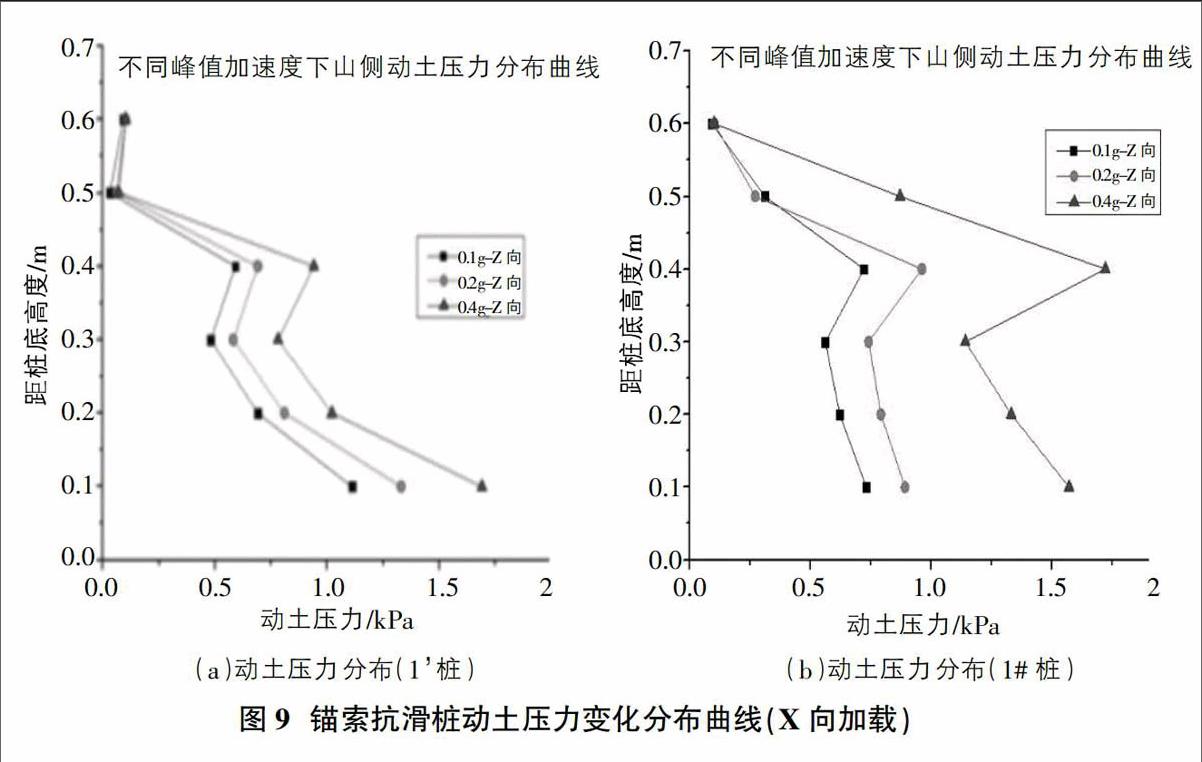
从图9可以看出：Z向单独加载时，当输入的动峰值加速度为0.4g时，单锚点与多锚点锚索抗滑桩动土压力都有了显著的增加，多锚点锚索抗滑桩最大值靠近桩底，值为1.72kPa：单锚点锚索最大值位于滑面处，值为1.67kPa。

同时，从图中可以看出，随着输入的EL-Centro波动峰值加速度的增大，单锚点与多锚点锚索抗滑桩山侧动土压力均不断增加，且动土压力分布规律略有不同。单锚点锚索抗滑桩，滑面以上，靠近桩顶部分动土压力较小，滑面附近动土压力值最大，且动土压力增幅较大：滑面以下，靠近桩底动土压力值最大。而多锚点锚索抗滑桩，滑面以上，动土压力值在滑面处最大：滑面以下，靠近桩底动土压力值最大，动土压力最大值位于桩底。

从图10可以看出：X向单独加载时，当输入的动峰值加速度为0.4g时，单锚点与多锚点锚索抗滑桩动土压力都有了显著的增加，多锚点锚索抗滑桩最大值靠近桩底，值为2.98kPa：单锚点锚索最大值位于滑面处，值为6.38kPa。

同时，从图中可以看出，随着输入的EL-Centro波动峰值加速度的增大，单锚点与多锚点锚索抗滑桩山侧动土压力均不断增加，且动土压力分布规律略有不同。单锚点锚索抗滑桩，滑面以上，靠近桩顶部分动土压力较小，滑面附近动土压力值最大：滑面以下，靠近桩底动土压力值最大。当输入的动峰值加速度为0.4g时，单锚点锚索抗滑桩动土压力有了显著的增加，最大值位于滑面处，值为6.38kPa。多锚点锚索抗滑桩，滑面以上，靠近滑面附近动土压力值最大；滑面以下，靠近桩底动土压力值最大，动土压力最大值则位于桩底。

从图11可以看出：XZ向单独加载时，随着输入的EL-Centro波动峰值加速度的增大，单锚点与多锚点锚索抗滑桩山侧动土压力均不断增加，动土压力分布规律略有不同。单锚点锚索抗滑桩，滑面以上，靠近桩顶部分动土压力较小，滑面附近动土压力值最大：滑面以下，靠近桩底动土压力值最大。当输入的动峰值加速度为0.4g时，动土压力有了显著的增加。多锚点锚索抗滑桩，滑面以上滑面附近动土压力值最大：滑面以下，靠近桩底动土压力值最大，动土压力最大值则位于桩底。

综上所述，当动峰值加速度不大于0.4g时，多錨点锚索抗滑桩的抗震效果较好。由于本次计算模型尺寸较小，滑体体积相对较小，使得滑坡推力较小，当多锚点锚索抗滑桩单根锚索的锚索拉力满足其工程条件时，多锚点锚索抗滑桩相当于给抗滑桩施加了多个可靠约束，能有效地控制坡体变形，使得抗滑桩变形较小。

2.4剪力计算结果分析

当输入的动峰值加速度不大于0.4g时，水平向振动效应要比垂直向显著。由于桩身剪力分布基本相同，因此本文以X向加载时，剪力随输入EL-Centro波动峰值加速度的分布变化进行分析。

图12为x向加载时，随着输入EL-Centro波动峰值加速的增大，锚索抗滑桩桩剪力的变化分布曲线图。图（a）可以看出：X向单独加载时，随着输入EL-Centro波动峰值加速度的增大，单锚点锚索抗滑桩在滑面处剪力不断增大，且在嵌固段出现负剪力。在设置锚索位置，随着输入的EL-Centro波动峰值加速度的增大，振动作用加剧，该处剪力略有减小，其分布规律基本相同。

图（b）可以看出：X向单独加载时，随着输入EL-Centro波动峰值加速度的增大，多锚点锚索抗滑桩在滑面处剪力亦不断增大，并且在抗滑桩的嵌固段局部出现负剪力，并随着输入的EI-Centro波动峰值加速度的增大，不断增加。由于多锚点锚索抗滑桩设有2排锚索，该处剪力较小，分布规律基本相同。总体而言，多锚点抗滑桩桩身弯矩相对较小。

2.5弯矩计算结果分析

由于，不同向加载时，单锚点与多锚点抗滑桩弯矩分布规律基本相似，同样以X向加载时，弯矩随输入EL-Centro波动峰值加速度的分布形式变化进行分析。

图13为X向加载时，随着输入EL-Centro波动峰值加速的增大，锚索抗滑桩桩弯矩的变化分布曲线图。图（a）可以看出：X向单独加载时，随着输入的EL-Centro波动峰值加速度的增大，单锚点锚索桩身弯矩不断增大，尤其在滑面处较快增大。并且在桩头部位出现反弯，其弯矩分布规律基本相同。

图（b）可以看出：X向单独加载时，随着输入EL-Centro波动峰值加速度的增大，多锚点锚索抗滑桩在滑面处弯矩亦不断增大，并随着输入的EL-Centro波动峰值加速度的增大，不断增加。但由于多锚点锚索抗滑桩设有2排锚索，桩头设置锚索部位弯矩较小，分布规律基本相同。总体而言，多锚点抗滑桩桩身弯矩相对较小。

3结论

本文运用ABAQUS有限元数值软件，建立单锚点与多锚点锚索抗滑桩加固边坡的三维有限元模型，进一步研究了在不同EL-Centro波动峰值加速度作用下，单锚点与多锚点锚索抗滑桩的抗震性能，并得出以下结论：

①从坡体的位移变形来看，输入相同的EL-Centro波动峰值加速度，X加载时的坡体水平位移比Z向加载时位移变化更明显，不利于边坡的稳定，且XZ双向加载时的坡体位移比单向加载要大。

②相同动峰值加速度作用下，多锚点锚索抗滑桩加固的坡体，其产生的位移相对较小，有利于控制坡体的变形，而且多锚点锚索抗滑桩桩身弯矩、剪力值相对较小。

③从锚索抗滑桩土压力分布曲线来看：多锚点滑面处动土压力相对较小，抗震性能较好。endprint