软土地区中庭式地铁车站动土正应力分布规律*

张志明 郭宗程 袁 勇

(1.贵州大学土木工程学院， 550025， 贵阳； 2.贵州省岩土力学与工程安全重点实验室， 550025， 贵阳；3.同济大学土木工程防灾国家重点实验室， 200092， 上海∥第一作者， 讲师)

车站侧墙动土正应力为地铁车站抗震研究中的重要指标。而当前的地铁车站动土正应力研究或仅描述其时程变化[1-2]，或仅给出其峰值动土正应力分布[3-6]，未能深入研究地铁车站侧墙动土正应力的实时分布及周期性变化。对此，本文以上海软土地区某中庭式地铁车站及场地为原型，搭建实体的土-地铁车站模型，在5 Hz谐波工况及Loma Prieta地震波工况下开展振动台试验，测试车站左右侧墙的动土正应力，研究地铁车站侧墙动土正应力的时程，以及周期内实时分布与峰值分布等响应规律。

1 振动台试验概况

1.1 原型车站及场地

原型场地自上而下依次为①1层填土、②1层粉质黏土、②3层砂质粉土、③1层淤泥质粉质黏土、⑤1层黏土和⑤3层黏土(土层序号参考DGJ 08-37—2012《岩土工程勘察规范》)。原型中庭式车站为地下两层岛式车站，宽21.3 m、高17.7 m，底板埋深与车站高度几乎相同。

1.2 试验设备和相似比

试验所用振动台的台面长4.0 m、宽4.0 m，可实现三向地震动输入。试验采用圆筒形柔性模型箱，其直径为3.0 m、高度为1.8 m。振动台和模型箱如图1所示[7]。人工模型土由砂与锯末混合制成[8-9]，其动力特性和原型场地土相似。原型车站为现浇钢筋混凝土结构，采用C35混凝土和HRB400钢筋。试验采用镀锌钢丝和微粒混凝土分别模拟原型钢筋和混凝土。

a) 振动台

基于实验室设备的承载能力，依据量纲分析进行振动台试验的相似比设计。本试验中，长度相似比取1/30、线位移相似比取1/30、加速度相似比取1.000、动剪切模量相似比取0.033、持时相似比取0.183、频率相似比取5.480、动应变相似比取1.000、模型结构和模型土的弹性模量相似比分别取0.420和0.033。通过对比动剪切模量比随剪应变变化曲线、阻尼比随剪应变变化曲线，可以看出模型土能较好的反应出原状土的动力特性。其他物理量的相似比、试验设计细节等详见文献[7,10]。

通过对比目标输入地震波和实际测得的振动台台面地震波，发现两者吻合较好，验证了振动台设备具有较好的工作性能[11]；通过对比自由场模型地表离模型箱侧壁不同距离测点的加速度、分析模型箱侧壁的位移，验证了柔性模型箱的剪切位移模式，模型箱的边界效应基本可以忽略[10,12]。

1.3 土压力计布置

土压力计测点布置于车站左、右侧墙上(如图2所示)，用于探测侧墙动土正应力的幅值和分布。

1.4 地震动输入

本研究采用谐波及地震波来研究地铁车站侧墙动土正应力的幅值和分布特征。谐波频率取5 Hz,地震波选用1989年10月18日美国加利福尼亚州Loma Prieta地震波。谐波与地震波的峰值均调整为0.1g(g为重力加速度)。谐波加速度时程见图3，地震波加速度时程和反应谱见图4。其中目标反应谱为依据GB 50011—2010(2016年版)《建筑抗震设计规范》针对原型场地(Ⅳ类场地、7度设防、设计基本加速度0.1g)获得的加速度反应谱。

图2 模型车站侧墙土压力计测点布置[7]Fig.2 Layout of soil pressure gauges on model stationside wall

图3 5 Hz谐波加速度时程曲线Fig.3 Acceleration time-history curve of harmonic waveinput of 5 Hz

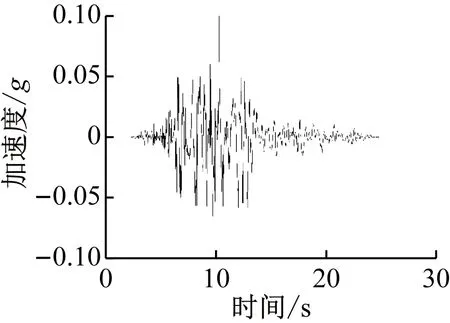
a) Loma Prieta波加速度时程曲线

2 动土正应力试验结果

2.1 动土正应力时程曲线

动土正应力定义为任一时刻车站侧墙的总应力与静土压力的差值：动土正应力为正值，说明该时刻的总应力大于地震动输入前的初始静土压力；动土正应力为负值，说明该时刻的总应力小于地震动输入前的初始静土压力。左右侧墙的受力情况类似，本文以左侧墙为例进行分析。

2.1.1 5 Hz谐波工况

在5 Hz谐波激励作用下，11个测点在振动持续时间tc为7.00～8.20 s时的动土正应力时程曲线见图5。由图5可知：最大动土正应力发生在PL1处 (侧墙底部)；与其他位置相比，PL3～PL6处(中板至底层中部)的动土正应力要小得多；所有动土

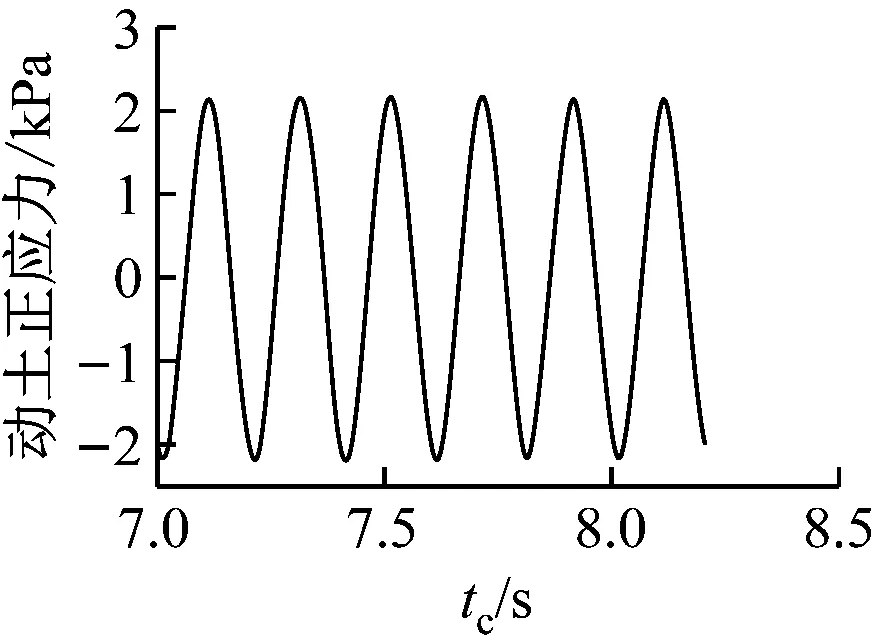
a) PL1测点

e) PL5测点

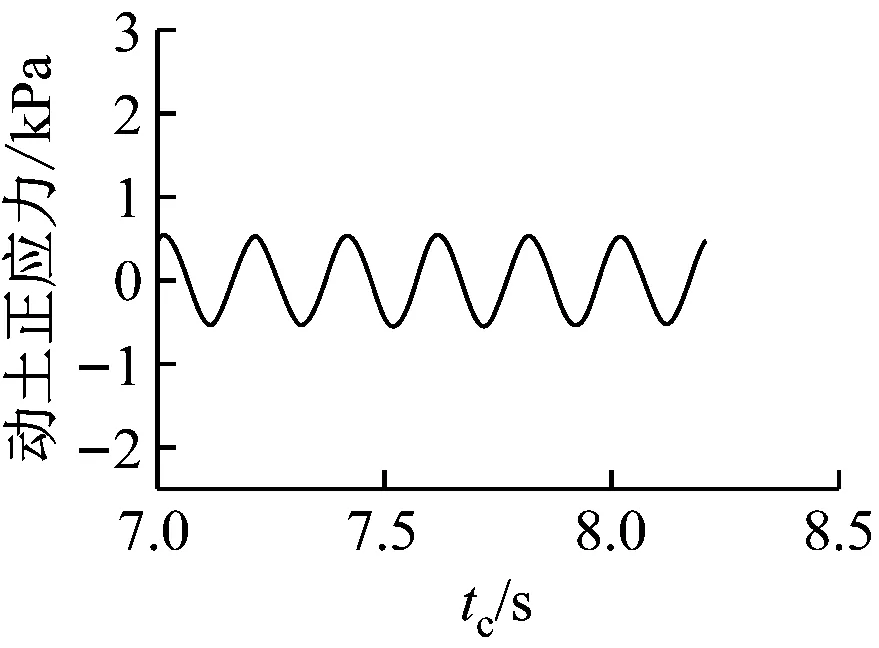
i) PL9测点

正应力的变化频率均为5 Hz，与输入谐波的频率一致。

2.1.2 Loma Prieta地震波工况

在Loma Prieta地震波激励作用下，11个测点在tc为4.00～6.00 s时的动土正应力时程曲线见图6。由图6可知：最大动土正应力也发生PL1处(侧墙底部)；PL3～PL6处(中板至底层中部)的动土正应力明显较小；动土正应力时程曲线与输入地震波形状相似。该现象印证了以加速度形式输入的地震动激励可以转换为应力波[13]。

2.2 周期内的动土正应力分布

2.2.1 5 Hz谐波工况

在5 Hz谐波工况下，为研究1个完整周期(0.20 s)内的侧墙动土正应力实时分布，本文以动土正应力最大的PL1测点为目标测点，以PL1测点的动土正应力峰值时刻tpk=7.52 s为基准，选取周期(T=0.20 s)内tpk-T/2=7.41 s、tpk- T/4=7.46 s、tpk=7.52 s、tpk+T/4=7.57 s、tpk+T/2=7.62 s等5个代表性时刻进行研究。图7为5个代表性时刻的侧墙动土正应力分布。

从图7可见左右侧墙的动土正应力分布规律：

1) 动土正应力具有显著的周期性。当t=7.41 s与t=7.62 s时，动土正应力几乎完全一样，分布曲线几乎重合。与之相比，t=7.52 s时的动土正应力绝对值相等，拉压方向相反。当t=7.46 s和t=7.57 s时，侧墙的动土正应力近似为零，侧墙受力处于平衡状态。

2) 当车站侧墙受力未处于平衡状态(t=7.41 s、t=7.52 s和t=7.62 s)时，动土正应力沿侧墙总体呈近似弧形分布；最大正应力发生在侧墙底。

3) 对比左、右侧墙的结果可以发现，在同一埋深处，左、右侧墙动土正应力绝对值相差很小;呈一拉一压状态。这与结构剪切变形(或称Racking)的状态相呼应，也与文献[14]的发现吻合。

2.2.2 Loma Prieta地震波工况

根据文献[10]，土-中庭式地铁车站系统的基频与自由场场地的基频一致，均为6.89 Hz。本文分析地震波工况下的动土正应力试验结果发现，动土正应力时程具有明显的周期性，所有测点动土正应力时程的一阶卓越频率均为6.89 Hz，与土-中庭式地铁车站系统的基本频率一致，则周期T1=1/6.89=0.14 s。

a) PL1测点

e) PL5测点

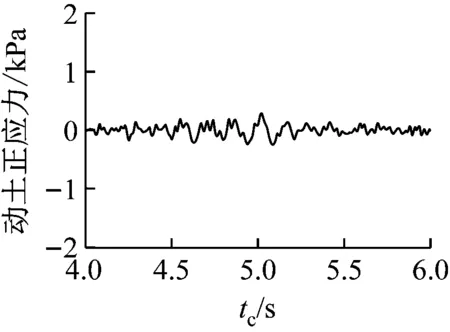
i) PL9测点

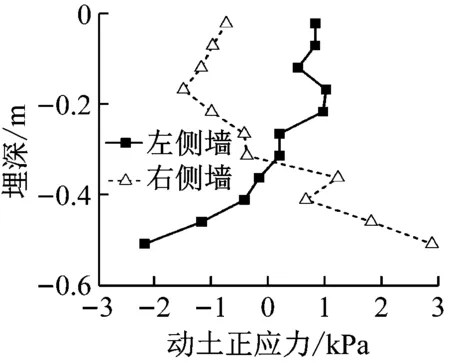
a) t=7.41 s

d) t=7.57 s

以动土正应力峰值时刻tpk=4.94 s为基准，则以1个完整周期T内t=4.87 s、t=4.91 s、t=4.94 s、t=4.98 s、t=5.01 s为代表性时刻的左、右侧墙动土正应力分布见图8。从图8可以看出：

1) 在Loma Prieta地震波激励下，左、右侧墙动土正应力分布表现出明显的周期性。t=4.87 s和t=5.01 s时的动土正应力分布曲线十分相似。与之相比，t=4.94 s时的动土正应力绝对值相等、拉压方向相反。t=4.91 s、t=4.98 s时动土正应力的数值很小，从地震波的周期角度可认为在这两个时刻车站侧墙处于平衡状态。这些规律也佐证了动土正应力时程的周期性。

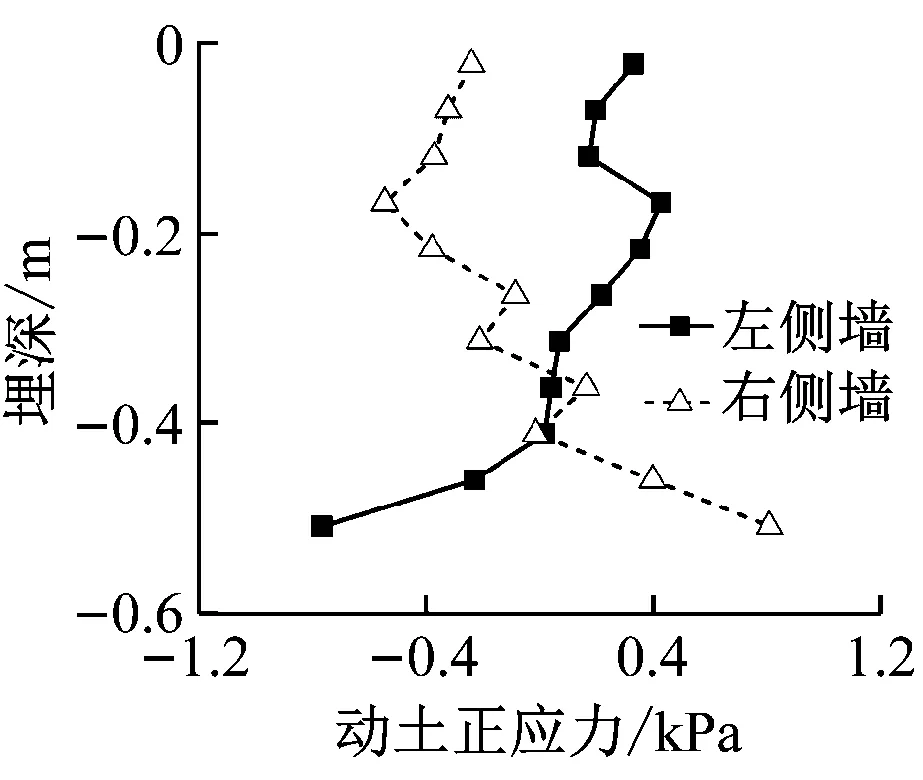
a) t=4.87 s

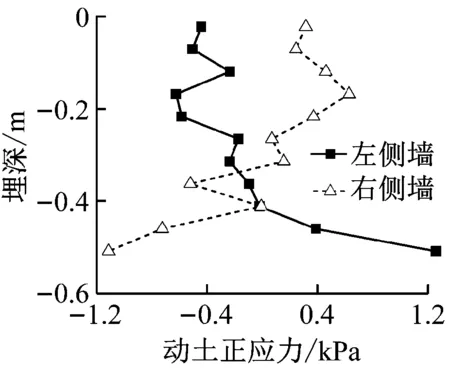
c) t=4.94 s

e) t=5.01 s图8 代表性时刻的动土正应力分布(Loma Prieta波)Fig.8 Dynamic soil normal stress distribution at fiverepresentative moments (Loma Prieta wave)

2) 与5 Hz谐波工况结果类似，当车站侧墙未处于平衡状态时(t=4.87 s、t=4.94 s和t=5.01 s)，动土正应力沿侧墙呈近似弧形分布。最大动土正应力同样发生在侧墙底。

3) 在同一时刻、同一埋深情况下，左、右侧墙的动土正应力大小近乎相等、方向相反，即同样呈现一拉一压的状态。

2.3 动土正应力峰值

2.3.1 5 Hz谐波工况

5 Hz谐波工况下，各测点动土正应力峰值的绝对值如图9所示。由图9可以看出：①整体上，左右侧墙的动土正应力峰值沿侧墙均呈近似“L”形分布；②最大动土正应力峰值发生在侧墙底；③在5 Hz谐波工况下，左、右侧墙的峰值动土正应力大小存在差异。

图9 5 Hz谐波峰值动土正应力

2.3.2 Loma Prieta地震波工况

图10为Loma Prieta地震波工况下的车站侧墙峰值正应力分布。与5 Hz谐波工况类似，在Loma Prieta地震波激励下，峰值动土正应力沿侧墙仍呈近似L形分布，最大动土正应力峰值仍发生在侧墙底,左、右侧墙动土正应力峰值几乎完全相同。

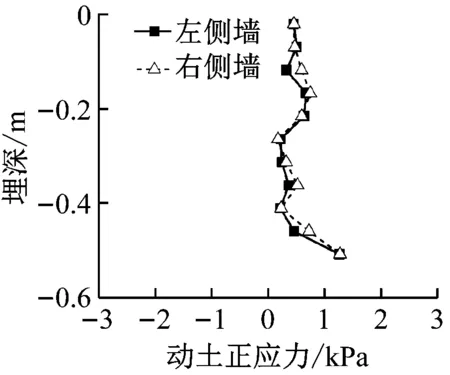
图10 Loma Prieta地震波峰值动土正应力Fig.10 Peak dynamic soil normal stress under LomaPrieta wave

2.3.3 动土正应力峰值与静止土压力比较

本文以右侧墙为例，分析动土正应力峰值与初始静止土压力的关系。表1为右侧墙静止土压力理论值和动土正应力峰值试验结果。

由表1可以看出，无论是谐波还是地震波工况，两者比值整体呈现侧墙顶部和底部较大，中间较小的趋势；在侧墙顶部，动土正应力增量相比初始静止土压力极其显著，谐波和地震波工况下两者比值甚至达到8倍和5倍。试验结果表明，地铁车站抗震设计中有必要考虑地震动输入对侧墙土正应力的放大效应。

3 结论

1) 在谐波激励及地震波激励下，侧墙动土正应力时程均具有典型的周期性。在5 Hz谐波工况下，侧墙动土正应力时程频率也为5 Hz；在Loma Prieta地震波工况下，侧墙动土正应力时程的一阶卓越频率与场地的一阶卓越频率一致。

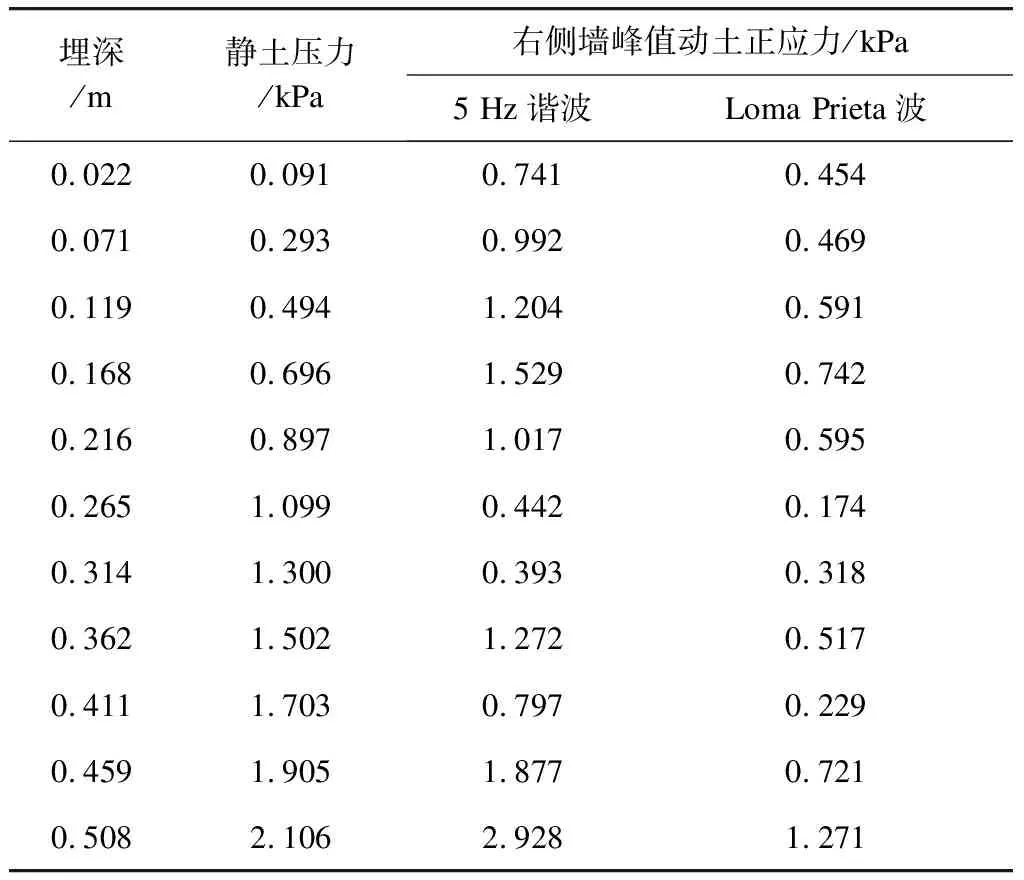
表1 动土正应力试验结果对比静止土正应力理论解

2) 无论是在谐波激励下还是地震波激励下，沿车站侧墙动土正应力峰值均整体呈近似L形分布；最大动土正应力均发生在侧墙底，且中板与底层层高中央范围的动土正应力要小得多。

3) 无论是在谐波激励下还是地震波激励下，在同一时刻、同一埋深处，中庭式地铁车站左、右侧墙的动土正应力绝对值相差很小,呈一拉一压状态。