基于PCA-MLR的公共建筑能耗报警阈值计算

林跃东，许巧玲，严哲钦

(福州大学节能技术研究中心，福建 福州 350116)

0 引言

建筑能耗监测系统被视为公共建筑的节能管理平台. 监测系统大都设置能耗越限报警功能，即当某一能耗测量值超过报警阈值时，系统报警，提醒操作人员观察(或调整)报警涉及设备的运行状态，以避免设备的异常运行导致不必要的能源消耗. 通常能耗阈值依据经验或理论计算得到，根据经验设定能耗阈值的方法在监测系统建设初期使用较广，但存在不足，有时设定的阈值与建筑用能系统的实际情况有偏差，影响报警功能的正常应用.

近年来，国内外学者对建筑能耗预测进行了大量的研究，采用的方法主要有：多元线性回归分析法、人工神经网络法、灰色理论法、支持向量机法等. 1980年，Parti等[1]率先将线性回归分析方法引入建筑能耗预测领域，采用线性回归法建立了建筑能耗预测模型，并使用该模型对圣地亚哥地区的建筑能耗进行了预测. Escrivá-Escrivá等[2]分析西班牙哥伦比亚大学的建筑能耗数据，以最高温度、最低温度、日均温度为输入建立了高校建筑能耗的神经网络预测模型. 徐聪麒[3]采用基于粒子群优化训练的RBF网络计算28栋办公建筑的日能耗报警阈值，并将结果用于能耗监管平台，该方法的应用减少了能耗监管平台的误报警情况； 王彦端[4]采用DeST模拟分析，选定外窗传热系数、室温、室内相对湿度、通风次数、建筑面积和竣工时间6个参数，以此为输入建立SPSO-BP高校用能定额计算模型，该方法的计算结果比统计学方法计算出的能耗结果误差更小. 以上方法都在实践中得到了验证，具有一定的应用价值. 但是，这些方法对所有样本数据采取统一分析，未考虑建筑物不同运行状况下用能数据间的差异，将其用于能耗报警阈值计算时精度不足.

本研究提出一种基于PCA-MLR的公共建筑能耗报警阈值计算方法，按照建筑的实际运行状况，对能耗进行分类处理，然后通过主成分分析，去除信息冗余，消除变量之间的相关性，提取主元，以简化建模过程. 在此基础上，建立不同类型能耗的多元线性回归模型，用于建筑能耗报警阈值的计算.

1 预备知识

1.1 主成分分析

建筑能耗的影响因素众多，且各变量之间存在一定的相关性，个别信息互有重叠，导致建模过程错综复杂. 研究采用主成分分析法(PCA)，构造几个互不相关的综合变量(主成分)，用以代替初始变量，力求减少自变量之间的多重共线性问题[5].

主成分表达式如下：

式(1)中：yi为主成分;x为随机变量矩阵;u为特征向量矩阵.

主成分表征信息的能力用方差贡献率表示：

方差贡献率越大，主成分表征信息的能力也越强.

1.2 多元线性回归

建筑能耗与影响因素的关系体现为一个因变量与多个自变量的关系. 回归分析法在分析多因素模型时，相比于其它分析方法更加简单和方便. 研究采用多元线性回归分析(MLR)，解释建筑能耗与众多影响因子之间的关系. 多元线性回归方程如下：

式中：β0为常数项(也称回归常数)，β1，β2，…，βp为回归系数；ε为随机误差；y为因变量；x1，x2，…，xp为自变量；p为自变量个数.

为获取最优的β0,β1, …,βp,σ2等未知参数，需对变量进行n次观测，则线性回归模型可表示为：

2 模型建立

2.1 总体流程

图1 基于PCA-MLR的能耗报警阈值计算模型流程图Fig.1 Flow chart of energy consumption alarm threshold calculation based on PCA-MLR

图1为建立基于PCA-MLR的能耗报警阈值计算模型的总体流程图. 具体过程为：首先对能耗样本数据进行预处理，消除数量级的差别，并依据建筑的运行状况，对能耗进行分类(一般办公建筑可分为工作日和节假日两类，商场建筑可分为营业时间和非营业时间两类，等). 通过主成分分析法处理输入变量，以去除信息冗余，消除变量之间的相关性，提取主元. 然后再采用多元线性回归方法，建立不同类型能耗的阈值计算模型.

通常能耗阈值每天更新一次. 采用同类别前一天相应计量点的能耗数据，按该类别模型计算得到报警阈值. 研究以一栋办公建筑为例，阐述基于PCA-MLR的公共建筑能耗报警阈值计算方法及应用.

2.2 模型建立

以该办公建筑空调季(2013年6月15日至8月31日)共78组的日能耗数据作为样本数据，其中前47个数据(6月15日至7月31日)作为训练样本，其余31个数据(8月1日至8月31日)作为检验样本. 建筑能耗数据量大，数值波动范围广，为减小预测误差，采用z-score规范法[6]对样本数据进行预处理. 然后将能耗数据分为工作日能耗和节假日能耗两类，分别对其进行分析.

影响建筑能耗的因素可分为3个方面：外部气候条件、建筑结构、工作状态[7]. 对于某一具体建筑来说，其建筑类型、建筑面积、建筑层数、窗墙比、建筑朝向等建筑本体因素固定不变，其对建筑能耗的影响相对固定； 建筑的工作状态、使用人数等条件也相对固定. 文献[8]指出建筑能耗随天气条件的变化波动较大，研究主要考虑天气条件对建筑能耗波动的影响，选取温度(x1)、露点温度(x2)、含湿量(x3)、气压(x4)、能见度(x5)、风速(x6)、降雨量(x7)、天气情况(x8)等8个天气指标作为输入参数. 其中天气情况采用天气特征值来表征[9].

图2 主成分碎石图Fig.2 Scree plot of principal component

以上8个天气因素之间存在一定的相关性，经z-score规范化处理后，8个变量之间的相关系数矩阵见表1，从表1中可以看出，每个变量至少与另一个变量的相关系数绝对值大于0.30，变量之间存在较强的相关性，适合使用主成分分析法.

主成分分析得到的碎石图见图2. 由图2可以得到，第1个主成分的特征值为3.295，其方差贡献率最大，达41.187%； 当主成分个数为5时，累计方差贡献率达91.501%(>90%)，主成分已经能代表样本的大部分信息. 因此，研究选取前5个主成分作为多元线性回归模型的自变量.

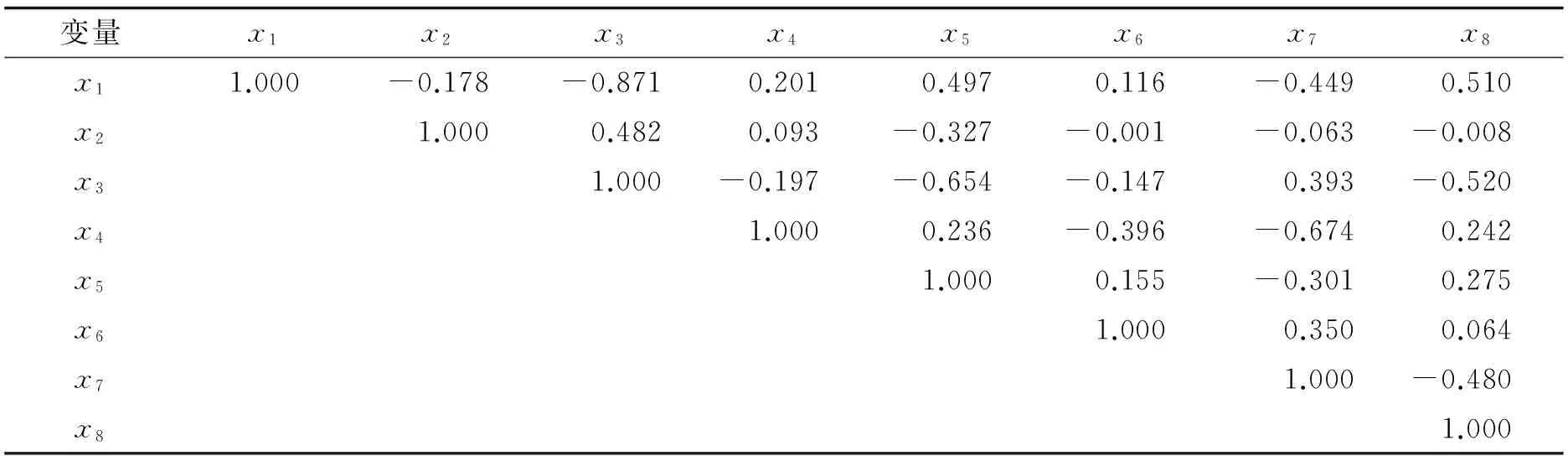
表1 相关系数矩阵

将上述5个主元作为自变量，建筑日耗电量作为因变量y，采用前文样本，建立了基于PCA-MLR的该办公建筑能耗报警阈值计算的模型. 其工作日模型为：

节假日模型为：

3 模型检验

首先采用F检验法对以上两个模型分别进行显著性验证，结果如表2所示，工作日模型的F统计量值为6.140，其第一自由度为5，第二自由度为27，置信度为95%时，查“F分布表”[10]得：F0.05(5, 27)=2.728 335. 故F=6.140﹥F0.05(5, 27)=2.728 335，即认为在α=0.05的显著性水平上线性回归方程显著； 同理，节假日模型检验结果为：F=3.785﹥F0.05(5, 8)=3.687 499，同样表明在α=0.05的显著性水平上回归方程具有显著的线性关系.

表2 回归方程检验统计量

该建筑能耗的单一MLR工作日模型如式(8)、节假日模型如式(9)所示.

ycluster1= 267.812x1+25.580x2+9.815x3+51.254x4+3.252x5+18.536x6-

ycluster2= -322.954x1+142.454x2-173.644x3-110.892x4-108.370x5+60.287x6-

以2013年8月份的31个日耗电量作为检验样本，其中工作日能耗22个，节假日能耗9个. 分别采用该建筑的PCA-MLR模型和单一MLR模型，进行2013年8月份日能耗预测，预测结果与实际能耗对比如图3所示.

图3 能耗预测对比图Fig.3 Comparison of prediction results

对于工作日能耗，PCA-MLR模型的相对误差为7.43%，单一的MLR模型为15.27%. 而节假日能耗的PCA-MLR模型的相对误差为8.69%，单一的MLR模型为16.58%. 相对误差的计算结果表明，PCA-MLR模型的预测精度优于单一的线性回归模型.

4 方法应用

图4 阈值设置界面Fig.4 Threshold setting interface

将方法用于上述办公建筑能耗监测系统，该系统可对计量点能耗、分项能耗、日能耗等进行阈值设置，图4为日能耗阈值设置界面截图. 根据预测值的95%预测区间设置能耗报警阈值的上下限，每日8时能耗阈值自动更新.

在一个月的观察期中，系统产生过一次报警，为上限超出. 报警日期为2015年9月6日(周日), 当天预测值为5 787.4 kW·h，其95%的置信区间为(5 343.6, 6 231.3)，所以其上限为6 231.3 kW·h.而实际能耗6 862.0 kW·h，超过阈值9.19%. 当天下午部分员工加班，照明灯具大范围开启，集中供冷系统整体处于运行状态，与通常休息日相比，能耗大大超限.

5 结语

基于PCA-MLR的公共建筑能耗报警阈值计算方法，首先根据建筑的使用情况对能耗进行分类，针对不同类别建立相应的能耗阈值计算模型，以期提高模型的拟合精度. 在建筑本体因素固定，使用情况不变的前提下，以8个天气指标作为初始变量，通过主成分分析，得到5个主元，以此为输入，分别建立该建筑各类别能耗的多元线性回归模型.

方法通用性强，准确性较高，可用于建筑能耗监测系统的阈值计算. 实例表明，采用本方法计算公共建筑能耗监测系统的能耗报警阈值，系统误报警少. 该方法的应用，强化了建筑能耗监测系统的报警性能.

[1] PARTI M, PARTI C. The total and appliance-specific conditional demand for electricity in the household sector[J]. Bell Journal of Economics, 1980, 11(1): 309-321.

[3] 徐聪麒. 基于粒子群优化的RBF网络在节约型校园能耗监管平台中的应用研究[D]. 南宁: 广西大学, 2012.

[4] 王彦端. 福建省高校建筑用能定能研究[D]. 福州: 福州大学, 2014.

[5] 许巧玲, 陈晓彦, 赵超, 等. 基于多元统计方法的酒店建筑能耗分析研究[J]. 福州大学学报(自然科学版), 2011，39(2): 249-253.

[6] 蔡维玲, 陈东震. 数据规范化方法对K近邻分类器的影响[J]. 计算机工程, 2010, 36(22): 175-177.

[7] 刘长军. 基于遗传BP神经网络技术的大型公建能耗分析模型的研究和应用[D]. 南宁: 广西大学, 2012.

[8] 张甫仁. 基于气象热舒适度的建筑能耗灰色神经网络预测[J]. 建筑科学, 2007, 23(10): 49-52.

[9] 张宝平. 基于遗传BP神经网络电力系统短期负荷预测[D]. 西安: 西安理工大学，2003.

[10] 梁飞豹, 吕书龙, 薛美玉, 等. 应用统计方法[M]. 北京：北京大学出版社，2010.