基于Spectral Tetris的单位模紧框架构造的新算法
2018-01-16燕亚娟朱玉灿
燕亚娟,朱玉灿
(福州大学数学与计算机科学学院,福建 福州 350116)
0 引言
1952年, Duffin等[1]在研究非调和Fourier级数的问题时,首次引入了Hilbert空间中的框架概念,并且初步讨论了框架的一些性质. Daubechies等[2]于1986年再次提出框架概念. 目前框架在信号处理、信号去噪[3]、数据压缩、采样原理、函数空间理论、通讯[4]等领域有许多重要的应用.
在实际应用中需要构造出具体的框架. 特别地,构造满足给定条件下的框架显得尤为重要. 近年来,有限维空间上的框架已经引起越来越多学者的重视. Casazza等[5]基于Schur-Horn定理,给出了满足特定条件下框架的存在性定理,该定理的证明方法提供了一种重要的框架构造思路. Rolli等[6]利用奇异值分解,给出了满足特定条件下框架的存在性定理,该定理从奇异值分解的角度,也提供了一种重要的构造框架的思路. 这些结论仅涉及框架的存在性的证明,并没有涉及如何系统地构造出具体的框架.
然而,对于给定性质的框架的构造仍然缺乏一些算法. Cahill等[7]提供了从已知框架算子的谱和向量的长度,构造出满足特定条件的框架的新方法,但是这种方法构造出的框架并不具有良好的稀疏性. Casazza等[8]第一次提出了一种用Spectral Tetris(谱块)来构造单位模紧框架的新的方法,基于谱块的思想构造出的算法是一个系统构造单位模紧框架的算法,使单位模紧框架的构造变得更容易. 另外由于用谱块构造出的框架具有很好的稀疏性,使其应用更有前景. 并且,自文献[8]发表后,基于Spectral Tetris构造框架方法的相关文献相继发表[9-13]. 文献[9]给出了基于Spectral Tetris的优先一阶谱块STC算法,其能构造N维空间中个数为M的单位模紧框架的充要条件.
文献[9]中构造单位模紧框架的算法思想是优先应用一阶谱块,当一阶谱块无法满足条件继续运行时就用二阶谱块. 但是,当N 本研究寻找构造N维空间的单位模紧框架的新算法,优先运用二阶谱块进行框架的构造,并且给出基于谱块的新算法(优先二阶谱块STC算法). 结果表明,优先二阶谱块STC算法能构造的单位模紧框架,优先一阶谱块STC算法却不能构造; 优先一阶谱块STC算法能构造的单位模紧框架,优先二阶谱块STC算法也能够构造. 首先简要介绍有限维Hilbert空间中框架的一些概念. Casazza等[8]为构造单位模紧框架引入了二阶谱块的概念.具体的定义和性质见文献[8]. 由于二阶谱块构造的框架具有很好的稀疏性,本研究考虑能否应用二阶谱块找到其他的算法来构造RN的单位模紧框架. 在构造单位模紧框架时,如果M,N不互素,则令(M,N)=P,即P表示M,N的最大公因数. 其中,M=PM1,N=PN1, (M1,N1)=1,P,M1,N1∈. 如果可以用M1,N1构造出单位模紧框架,且构造出的单位模紧框架的合成算子对应的矩阵记为F. 那么,N维空间上由M个单位向量也能构造出单位模紧框架,且构造出的单位模紧框架的合成算子对应的矩阵以P个F块构成. 即具有如下形式: 所以,对于单位模紧框架的构造只需考虑当M,N互素即(M,N)=1的情况.下面给出新算法. 注1实现优先二阶谱块STC算法的代码中,算法进行编码时,首先需要给定一个N×M的全零矩阵,用来存储最终输出的框架的合成算子对应的矩阵. 上述优先二阶谱块STC算法是关于谱不小于2时框架构造对应的新算法. 当算法的编码5, 6中en+1前边的系数的平方和不大于所给定的框架算子的特征值λn+1的值,以及满足框架的存在性定理时,则当N 为方便下述定理的证明,首先给出M≥2N时的相关结论. 在用优先二阶谱块STC算法来构造单位模紧框架时,优先二阶谱块STC算法中的每次循环后生成的矩阵就是一个推广预单位模紧框架的合成算子对应的矩阵. 所以为证明当M≥2N时,优先二阶谱块STC算法能构造单位模紧框架. 现给出关于推广预单位模紧框架的相关结论,即如下的定理1. 2) 若λ-2<ω<λ. 3) 若ω=λ. 1) 当ω≤λ-2,有m0=(n0-1)λ+ω≤(n0-1)λ+λ-2≤(N-1)λ+λ-2=M-2. 所以m0 2) 当m0=(n0-1)λ+ω,有ω=m0-n0·λ+λ; 当λ-2<ω<λ,有λ-2 ① 若n0 ② 若n0=N,则0 当ω=λ,n0 为方便下述定理2的证明,引入如下引理. 引理1[9]实矩阵T=T(x,a1,a2)满足二阶谱块的概念Ⅰ)、Ⅱ)、Ⅲ)的充要条件为: 其中:a1,a2≥0,分别为插入的二阶谱块的列的元素的平方和,且x为插入的二阶谱块的第一行的元素的平方和. 下面就给出优先二阶谱块的STC算法能够构造当N Ⅱ)M≥2(N-1). 再证Ⅱ)⟹Ⅰ).由于M≥2(N-1),且N 综上所述,定理成立. 证毕. Ⅱ)M≥2(N-1). 现证Ⅰ)⟹Ⅱ). 因为优先二阶谱块STC算法能够构造单位模紧框架. 假若算法首次运行时,插入的是一个二阶谱块,则1≤λ<2,即N≤M<2N. 由定理2的必要性可知M≥2(N-1). 假若算法首次运行时,插入的是一个一阶谱块,则λ≥2,即M≥2N. 因此,优先二阶谱块STC算法能够构造单位模紧框架,则M≥2(N-1). 即定理得证. 推论2已知M,N∈,且λ=,(M,N)=P(M1,N1),(M1,N1)=1, 则下面两个叙述等价. Ⅱ)M≥2(N-P). 注2优先二阶谱块STC算法所得的结论改进了优先一阶谱块STC算法的相关结论. 关于冗余度不小于2的框架的构造,由优先二阶谱块STC算法和优先一阶谱块STC算法验证都成立. 冗余度小于2的框架的构造,由于优先一阶谱块STC算法能构造单位模紧框架,则优先二阶谱块STC算法也一定能构造. 接下来用实例分别说明:优先二阶谱块STC算法能构造的单位模紧框架,却不能被优先一阶谱块STC算法所构造. 例1优先二阶谱块STC算法构造6维空间、向量个数为8的单位模紧框架的合成算子对应的矩阵. 由于(8, 6)= 2(4, 3),所以先考虑维数为3、向量个数为4时的单位模紧框架的合成算子对应的矩阵情况. 由优先二阶谱块STC算法可知, 此时得到的合成算子对应的矩阵为 又因为不存在L∈使得λ==,所以由命题知:优先一阶谱块STC算法不能构造维数为6、向量个数为8的单位模紧框架. [1] DUFFIN R J, SCHAEFFER A C. A class of nonharmonic Fourier series[J]. Transactions of the American Mathematical Society, 1952, 72(2): 341-366. [2] DAUBECHIES I, GROSSMANN A, MEYER Y. Painless nonorthogonal expansions[J]. Journal of Mathematical Physics, 1986, 27(5): 1 271-1 283. [3] BODMANN B G, LIPSHITZ S P. Randomly dithered quantization and sigma-delta noise shaping for finite frames[J]. Applied and Computational Harmonic Analysis, 2008, 25(3): 367-380. [4] STROHMER T, HEATH R W. Grassmannian frames with applications to coding and communications[J]. Applied and Computational Harmonic Analysis, 2003, 13(3): 257-275. [5] ANTEZANA J, MASSEY P, RUIZE M,etal. The Schur-Horn theorem for operators and frames with prescribed norms and frame operator[J]. Illinois Journal of Mathematics, 2007, 51(2): 537-560. [6] ROLLI W J. Constructing frames for finite dimensional Hilbert spaces[J]. Journal of Mathematical Analysis and Applications, 2006, 321(1): 388-395. [7] CAHILL J, FICKUS M, Mixon D G,etal. Constructing finite frames of a given spectrum and set of lengths[J]. Applied and Computational Harmonic Analysis, 2013, 35(1): 52-73. [8] CASAZZA P G, FICKUS M, MIXON D,etal. Constructing tight fusion frames[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 175-187. [9] CASAZZA P G, HEINECKE A, KORNELSON K. Necessary and sufficient conditions to perform Spectral Tetris[J]. Linear Algebra and Its Applications,2013, 438(5): 2 239-2 255. [10] CASAZZA P G, FICKUS M, HEINECKE A,etal. Spectral Tetris fusion frame constructions[J]. Journal of Fourier Analysis and Applications,2012,18(4):828-851. [11] LEMVIG J, MILLER C, OKOUDJOU K A. Prime tight frames[J]. Advances in Computational Mathematics, 2014, 40(2): 315-334. [12] 李登峰, 刘子胜. 基于Spectral Tetris算法的框架的最佳稀疏性[J]. 中国科学(数学), 2014, 44(10): 1 091-1 098. [13] CASAZZA P G, JESSE P. Weighted fusion frame construction via Spectral Tetris[J]. Advances in Computational Mathematics, 2014, 40(2): 335-351.1 预备知识




2 主要结果及其证明



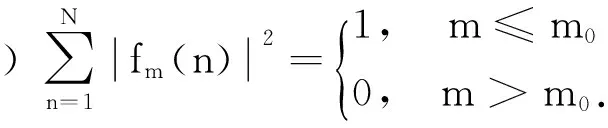

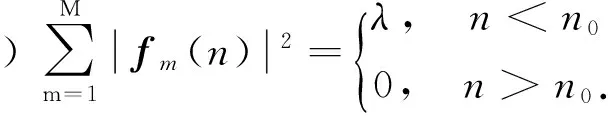









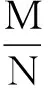

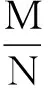
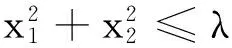


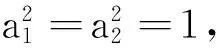
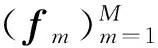
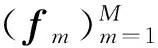
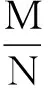
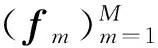
3 实例
