函数型数据下条件分位数的经验似然推断

熊贤祝, 周培钦

(福州大学数学与计算机科学学院, 福建 福州 350116)

0 引言

函数型数据分析的基本思想, 是把观测到的数据看成一个整体也就是将数据看作无穷维函数空间中的元素来进行处理和分析. 随着测量技术的发展, 在诸如医学诊断、气象预报、心理学、经济学以及生命科学等领域中都出现了函数型数据的统计问题, 函数型数据的分析方法在科学研究中显得越来越重要. 关于函数型数据的分析方法和最新进展可参考文献[1-3], 本研究主要考虑条件分位数. 众所周知, 对于重尾的误差分布以及异常值而言, 条件分位数是稳健的. 当数据是有限维时, 条件分位数的统计问题已经被很多文献所研究, 而在函数型数据下却较少研究. Ferraty 等[4]考虑了条件分布函数的NW估计, 建立了估计的完全收敛性并将结果应用到条件分位数.在独立和相依函数型数据下, 文献[5-6]均得到了条件分位数的核估计的渐近正态性并构造了正态逼近的置信区间.

就构造置信区间而言, 经验似然方法得到了很多的应用, 该方法由文献[7-8]提出, 与正态逼近方法相比有许多的优点(见文献[9]). 比如, 由数据来决定置信区间的形状, 而用正态逼近方法时, 其置信区间是对称的, 需要特别指出的是, 该方法不用估计渐近方差. 所以经验似然方法被广泛地用来构造各种未知参数的置信区间(见文献[10]). 在有限维数据下, 秦永松等[11]在有附加信息及没有附加信息时应用经验似然方法分别研究了条件分位数置信区间的构造, 随后Liang[12]把文献[11]的结果延伸到左截断模型.

本研究将文献[11]的结果延伸到函数型数据情形即在函数型数据下应用经验似然方法来考虑条件分位数的置信区间. 在适当的条件下得到了经验似然比统计量渐近服从χ2(1).

1 方法和主要结果

∀y∈,

对固定的p∈(0, 1), 给定X1=x条件下Y1的p分位数θp(x)为

如果F(y|x)关于y连续, 那么F(θp(x)|x)=p.

在后面的条件A1)、A2)和A3)下, 由文献[5]的引理2可知

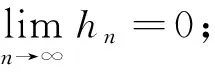
由此可设经验似然的得分函数

经验似然比定义为

经验似然比统计量为

其中:λ(θp(x))满足

A1) 存在三个函数g(·)、φ(·)(设单调不降, 且φ(hn)→0)和ζ0(·)使得

Ⅰ)Fx(hn)=g(x)φ(hn)+o(φ(hn)), 其中g(x)>0.

A2) 核函数K是一密度函数, 其紧支撑为[0, 1]且在[0, 1)上一阶导数连续. 其中，K(0)>0,K(1)>0, 且对∀t∈[0, 1],K′(t)存在且K′(t)<0.

A3) Ⅰ) 存在两个正数β和ν使得, ∀(y1,y2)∈2, ∀(x1,x2)∈U(x)×U(x), 有其中U(x)是x的某个领域,Cx是与x有关的一个正常数.

Ⅱ) ∀t∈,H′(t)存在且有界,∞.

注1这里的条件A1)～A4)与文[5]中的A1)～A4)完全一样. 条件A1)中 I)反映了函数型随机变量Xi分布的集中程度, 在函数型数据下的非参数回归分析中起着重要的作用. 另外, 文献[13]列举了一些满足条件A1)的例子. 条件A2)和A4)是关于核函数和窗宽的条件, 在函数型数据下的非参数回归分析是常见的.文献[4]用到了条件A3)的 I), 另外由常见的核函数所得到的分布函数会满足条件A3)的II).

主要结果如下.

定理1如果条件A1)～A4)成立. 那么

注2设zα满足P(χ2(1)≤zα)=1-α, 0<α<1. 由式子(9)可知θp(x)的名义置信水平为1-α的渐近经验似然置信区间：

2 定理的证明

首先引进一些引理.

引理11) 设条件A1)～A4)成立. 则对∀y∈, 有

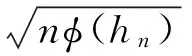
其中

及

2) 设条件A1)～A4)成立. 则

注3式(11)成立可由文献[5]中定理1推得, 而式(12)成立则由文献[5]中的引理2和引理3推得.

引理2设条件A1)～A4)成立. 则

证明 1) 由式子(11)和F(θp(x)|x)=p可推得

由式子 (12)、(16)和Slutsky定理可得

即式子(13)成立.

2) 分解式子(14)的左边项

设对∀u∈,Q(u)=, 其中则(u)du=1. 因此函数Q(·)也是核函数, 且Q满足核函数K的条件A2), 所以由引理2可得:

即

同理由引理1中1)可得

其中

又H2也是分布函数且满足分布函数H的条件A3)中的Ⅱ), 所以由引理1可得

由式子(19)～(20)可得

也就是

由条件A4)中I)可推出nφ(hn)→∞, 所以,

再由式子 (17)～(22)可得

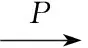
最后由式子(17)、(23)可推得式子(14)成立.

3) 对∀ε>0,

类似于文献[5]中引理1的证明可得

1) 先证

那么

由式子(13)可得

由式子 (14)～(15)以及式子(27)～(28)可得

2) 证明

由式子 (8)可得

设Ui=λ(θp(x))ωni(θp(x)), 1≤i≤n. 由式子(15)和(26)可得

由式子 (14)、(15)、(26)和(31)可推出式子(30)右边第三项的上界为

因此, 由式子(14)、(30)和(32)可推得式子(29)成立.

3) 由式子(31)可得

这里ηi满足: 存在C>0使得

由式子 (14)、(15)和(26)可得

注意到Ui=λ(θp(x))ωni(θp(x)), 1≤i≤n, 由式子(7)、 (26)、 (28)、 (29)以及式子(33)～(35)有

最后, 由式子 (13)、(14)和(36)推得定理1.

[1] RAMSAY J, SILVERMAN B W. Functional data analysis[M]. New York: Springer -Verlag, 2005.

[2] FERRATY F, VIEU P. Nonparametric functional data analysis: theory and practice[M]. New York: Springer-Verlag, 2006.

[3] FERRATY F, ROMAIN Y. The Oxford handbook of functional data analysis[M]. New York: Oxford University Press, 2011.

[4] FERRATY F, LAKSACI A, VIEU P. Estimating some characteristics of the conditional distribution in nonparametric functional models[J]. Statistical Inference for Stochastic Processes, 2006, 9(1): 47-76.

[5] EZZAHRIOUI M, OULD-SAID E. Asymptotic normality of the kernel estimators of the conditional quantile in the normed space[J]. Far East Journal of Theoretical Statistics, 2008, 25(1): 15-38.

[6] EZZAHRIOUI M, OULD-SAID E. Asymptotic results of a nonparametric conditional quantile estimator for functional time series[J]. Communications in Statistics-Theory and Methods, 2008, 37(17): 2 735-2 759.

[7] OWEN A B. Empirical likelihood ratio confidence intervals for a single functional[J]. Biometrika, 1988, 75(2): 237-249.

[8] OWEN A B. Empirical likelihood ratio confidence regions[J]. Annals of Statistics, 1990, 18(1): 90-120.

[9] HALL P, LASCALA B. Methodology and algorithms of empirical likelihood[J]. The International Statistical Review, 1990, 58(2): 109-127.

[10] CHEN S X, KEILEGOM I V. A review on empirical likelihood methods for regression[J]. Test, 2009, 18(3): 415-447.

[11] 秦永松, 苏淳. 条件分位数的经验似然置信区间[J]. 数学年刊, 2000, 21(2): 231-240.

[12] LIANG H Y, UNA-ALVAREZ J D. Empirical likelihood for conditional quantile with left-truncated and dependent data[J]. Annals of the Institute of Statistical Mathematics, 2011, 63(2): 267-289.

[13] FERRATY F, MAS A, VIEU P. Nonparametric regression of functional data: nference and practical aspects[J]. Australian and New Zealand Journal of Statistics, 2007, 49(3): 267-286.