序列一阶自相关对MK突变检验影响的探讨

王建新,王 健(山东理工大学 数学与统计学院,山东 淄博 255049)

时间序列的突变检验在生活中很多领域有着重要的应用，例如水文气象序列的突变时间研究.随着全球气候的变化威胁着人类的生活环境，关于水文气象序列的研究越来越重要.非参数统计方法要求的假定条件较少，运算比较简单，更容易使研究者理解应用推广.因此，研究非参数统计检验方法有重要的意义.目前关于突变检验的非参数统计方法有很多，如Mann-Kendall法，pettitt 法，Reverse Spearman’s rho test ,pettitt 法，WMW法等. 众所周知，非参数秩检验受原始数据是否存在自相关的先验假设条件限制，但高阶自相关远远小于一阶自相关带来的误差可以忽略.许多学者也认识到非参数统计法方法会受到一些序列自身性质的影响，而倾向研究小波理论等引入的新方法.[1-3]本文将通过蒙特卡洛模拟的方法验证剖析不同一阶自相关系数的存在对Mann-Kendall突变检验产生的具体差异影响，从而对其进行修正,并探讨不同样本空间所带来的的突变次数的改变.为检验相关问题提供更加简单可行的分析方法及运算步骤.

1 Mann-Kendall 突变检验

设时间序列{Xt},观察值序列{xt,t=1,2,...,n}.构造秩序列

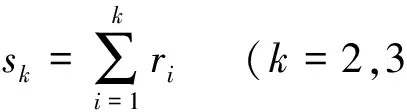
其中

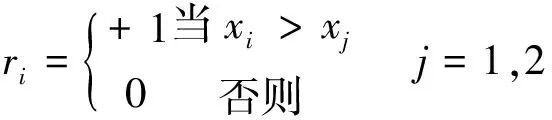
在时间序列随机独立的假定下，定义统计量：

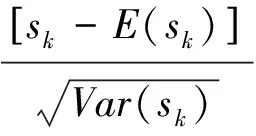
(k=1,2,...,n)

其中UF1=0，当x1,x2,...,xn相互独立，且连续同分布，

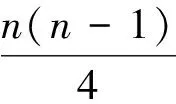
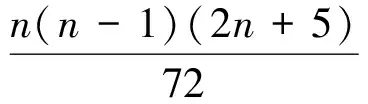
UFk是按时间序列x顺序x1,x2,...,xn计算出来的统计量序列.按时间序列x逆序xn,xn-1,...,x1,再重复上述过程，然后使计算值乘上-1，即可得到UBk序列.分别绘制UFk和UBk曲线图，如果UFk和UBk曲线交点在置信线之间，那么交点对应的时刻便是突变开始的时间.

2 AR(1)过程的影响

2.1 模拟条件

为了验证存在一阶自相关对于Mann-Kendall 突变检验方法产生的影响，将利用蒙特卡洛模拟实验对于不同一阶自相关系数ρ1的序列进行分析[4-5].设

Xt=μX+ρ1(Xt-1-μX)+εt

(1)

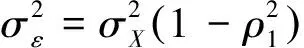
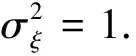
(2)

2.2 模拟结果及分析

蒙特卡洛模拟如图1、图2所示.

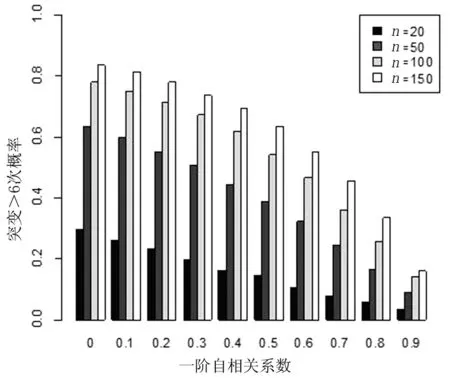
图1 正相关AR(1)影响结果Fig. 1 Effect of positive serial correlation

图2 负相关AR(1)影响结果Fig. 2 Effect of negative serial correlation

通过图1和图2可以看出，当时间序列存在正相关AR(1)过程时，随着正相关系数的不断增加，检验出突变次数呈明显的逐渐下降趋势.另外，随着样本空间的增大，检验出突变点的概率均随着增高，这符合现实的认知.当时间序列存在负相关AR(1)过程时，随着负相关强度的增加，检验出突变次数和正相关情况相反呈逐渐上升的趋势.通过对比不难发现，存在负相关AR(1)过程的样本要比存在正相关AR(1)过程的样本检验出突变的次数的概率均有所增加.因此，通过模拟实验不难发现如果时间序列存在自相关性对Mann-Kendall 突变检验方法将产生较大的影响，消除时间序列的自相关性在进行突变检验可能会产生更加精确的结果.

下面利用Pre-whitening法对蒙特卡洛模拟产生的时间序列进行预处理，然后再进行模拟实验.

3 Pre-whitening 处理

Pre-whitening法[6]是von Storch 提出，并被Yue S等人用于减少AR(1)过程对于MK检验趋势分析产生的影响中，下面验证其在处理突变检验中的效果.样本序列可以通过公式进行Pre-whitening处理：

Yt=Xt-ρ1Xt-1

然后对新的时间序列{Yt}进行蒙特卡洛模拟.

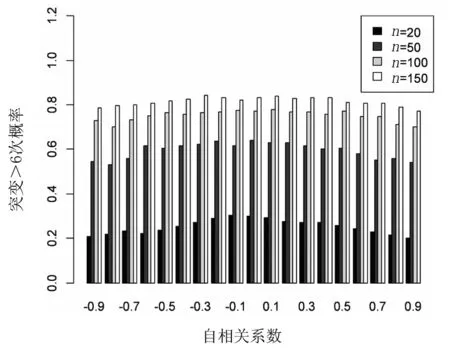
图3 Pre-whitening 修正Fig. 3 Modified by Pre-whitening

从图3可以看出，运用Pre-whitening 处理后的时间序列再进行蒙特卡洛模拟的Mann-Kendall突变检验已经去除了不同自相关系数对于突变检验的影响，各个样本空间的模拟实验结果均和自相关系数等于0时保持在几乎同一水平.说明Pre-whitening 处理对于Mann-Kendall突变检验也是一种有效的方法.

4 实例分析

以全国1949-2008年洪灾数据为例，利用非参数统计检验方法Mann-Kendall突变检验进行修正前后分析结果的分析对比.首先，判断洪灾数据是否存在一阶自相关性.

表1 一阶自相关系数显著性检验
Tab.1 The test of significance of lag-1 serial correlation coefficient

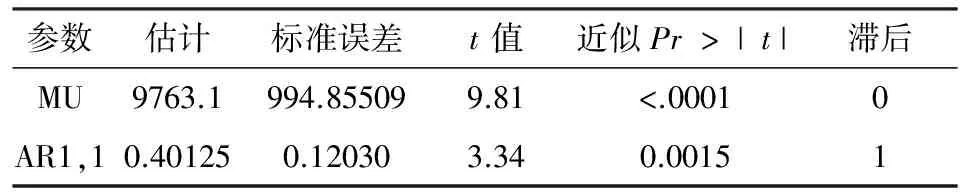
参数估计标准误差t值近似Pr>|t|滞后MU9763．1994．855099．81<．00010AR1，10．401250．120303．340．00151

通过利用SAS软件进行条件最小二乘估计(见表1).可以看出一阶自相关系数0.40125，并且系数的t检验p值小于0.01，说明该序列具有较强的一阶自相关性，系数显著非零，该数据具有一定的讨论意义.利用Pre-whitening 处理洪灾数据，消除一阶自相关对数据检验的影响.

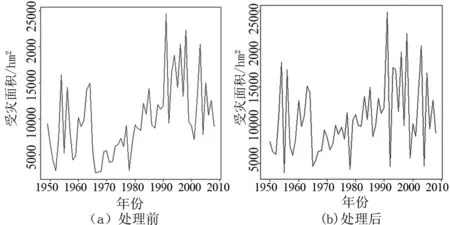
图4 全国1949—2008年洪灾数据Pre-whitening 处理前、后折线对比图Fig. 4 Line chart of flood data before and after Pre-whitenhg from 1949 to 2008 in China

利用pre-whitening 处理全国洪灾数据后，消除了数据本身存在的一阶自相关性.通过图4的折线图对比可以看出，数据处理前后波动起伏变化非常小，没有改变原始数据的核心信息.同时更好的满足了利用非参数秩检验方法所受到原始数据是否存在自相关的先验假设条件.

图5 全国1949-2008洪灾数据Pre-whitening 处理前、后MK突变检验对比图Fig. 5 Line chart of the MK test based on the flood data before and after Pre-whitenhg from 1949 to 2008 in China

Mann-Kendall突变检验，如果UFk和UBk曲线交点在置信线之间，那么交点对应的时刻便是突变开始的时间.从图5可以看出全国1949-2008洪灾数据Pre-whitening 处理前后的Mann-Kendall突变检验结果有所差异.因已算出原始数据一阶自相关系数ρ1=0.401 25，观察第三节中所做的不同一阶自相关系数在不同样本空间下对Mann-Kendall突变检验产生影响的分析结果，可以看出存在ρ1=0.4的不同样本空间下均会产生突变次数少许降低的影响. 对图5分析可以看出数据处理前Mann-Kendall突变检验只检验出1980年左右一次明显的突变，但数据处理后发现在原有的突变点外还有较小的波动，这对分析数据即会产生影响.同时将随着一阶自相关系数的增加以及样本量的变化产生更大的影响，更对剖析突变的成因，突变开始的时间点及突变的发展趋势等产生干扰，因而不容忽视. 通过修正的Mann-Kendall突变检验可以看出1980年前后发生了2次突变，其中1980年左右发生的突变最为显著，使全国洪灾受灾面积呈上升的趋势.不难发现靠前的一次突变可能是1980年突变产生的根源所在，值得引起我们的深入分析. 因此通过Pre-whitening 处理后的Mann-Kendall突变检验方法对进一步分析全国洪水灾害变化的趋势以及产生的原因可以做出更加精确的解释.

5 结束语

通过蒙特卡洛模拟实验可以看出，存在AR(1)过程的时间序列，在进行Mann-Kendall突变检验时会对检验的结果产生影响.并且不同的自相关系数对分析结果影响程度不同，可以分别从正负自相关系数来解释.因此，在利用Mann-Kendall突变检验方法检验时间序列的实际应用中，应先判断时间序列是否存在自相关性.本文利用蒙特卡洛模拟实验验证了Pre-whitening 处理方法在Mann-Kendall突变检验时间序列中修正的可行性.另外，通过实验不难看出，当一阶自相关系数ρ1≥0.2时，即将对Mann-Kendall突变检验结果产生不可忽视的误差.同时，当样本量n≥100，一阶自相关系数-0.1<ρ1<0.1时，为了计算简便可以忽略其误差.当一阶自相关系数ρ1≤-0.2时，Mann-Kendall突变检验结果也产生不可忽视的误差. Mann-Kendall突变检验方法适用于多类时间序列的突变检验，可以推广到其他水文气象领域或金融等领域的应用问题中，具有重要的研究及应用价值.

[1] 魏凤英. 现代气候统计诊断与预测技术[M]. 北京：气象出版社, 1999.

[2] 张应华, 宋献方. 水文气象序列趋势分析与变异诊断的方法及其对比[J]. 干旱区地理, 2015, 38(4): 652-665.

[3] 王振龙, 陈玺, 郝振纯, 等. 淮北平原水文气象要素长期变化趋势和突变特征分析[J]. 灌溉排水学报, 2010, 29(5): 52-56.

[4] YUE S, PILON P, PHINNEY B.et al. The influence of autocorrelation on the ability to detect trend in hydrological series[J]. Hydrol Processes, 2002,16：1 807-1 829.

[5] YUE S, WANG C Y. The Mann-Kendall test modified by effective sample size to detect trend in serially Correlated Hydrological Series[J]. Water Resour Manage, 2004,18：201-218.

[6] YUE S, WANG C Y. The applicability of pre-whitening to eliminate the influence of serial correlation on the Mann-Kendall test[J]. Water Res,2002, 38(6), 10.1029/2001WR000861, 4-1-7.

[7] 姚欣明, 陈元芳, 顾圣华, 等. EEMD-NNBR模型在降水预测中的应用[J]. 水电能源科学, 2014, 32(12): 11-13,16.