一种加8项余弦窗FFT的谐波检测方法

周爱华，姜雪菲(.哈尔滨理工大学 电气与电子工程学院，黑龙江 哈尔滨 50000；.青岛大学 自动化与电气工程学院， 山东 青岛 6607)

在电力系统中，由于大量非线性负荷的广泛应用，电网中产生了大量的各次谐波，从而使电能质量下降，不利于电力系统的安全和经济运行.为了能够更加有效地降低电网谐波对电网的影响[1]，提高电能质量，准确检测电网中的谐波成分是至关重要的.

在实际工程应用中，加余弦窗插值FFT算法[1-5]是用于电网谐波检测的较为广泛的方法之一.由于电网信号频率存在波动，往往很难实现对电网信号的同步采样.传统的FFT谐波检测算法对于谐波信号的检测精度低，存在着较大的误差.在这种情况下，应用传统的FFT算法检测谐波往往会导致频谱的泄露，从而使检测到的信号参数(频率、幅值、相位)存在较大误差，无法满足精确地检测谐波要求.由于采用硬件电路很难实现同步采样的局限性，加余弦窗FFT插值谐波检测算法采用旁瓣性能优良的窗函数有效地避免了传统的FFT谐波检测算法因频谱泄露带来的测量误差，极大的提高了谐波的检测精度，有助于电网中谐波的治理.采用具有不同旁瓣特性的余弦窗函数对频谱泄露有不同的抑制效果，比较常见的窗函数有Hanning窗、Hamming窗、Blackman窗、Blackman-Harris窗[6-9]等.一般常用的插值方法有双谱线插值法、三谱线插值法，它们在一定程度上有效地提高了谐波检测精度.本文充分考虑谐波频点附近的四根谱线包含大量的幅值信息的特点并对其进行加权处理， 能够进一步提高了谐波检测精度.

一般而言，改善窗函数的特性有助于进一步提高加窗插值算法的计算精度,同时又要考虑到算法的实时性.采用的项数少的窗函数虽然计算量小算法的实时性高，但不能够有效地抑制频谱泄露，提高谐波的检测精度；采用的项数较高的窗函数虽然可以有效提高检测精度，但是会导致谐波检测算法的实时性差.因此，本文在分析了不同余弦窗函数的特性后，利用MATLAB软件对加余弦窗插值FFT算法进行仿真，通过仿真数据的对比分析提出了一种性能优良的加8项余弦窗窗的谐波检测方法.本文在分析8项余弦窗函数特性的基础上，推导了基于8项余弦窗插值公式，并且利用MATLAB软件对该算法进行仿真.仿真结果表明，该算法能够有效地减小测量误差，提高信号参数(频率、幅值、相位)的检测精度，有利于电网谐波信号分析.

1 余弦窗函数及其特性

余弦窗的表达式为

(1)

式中n=0,1,...,N-1

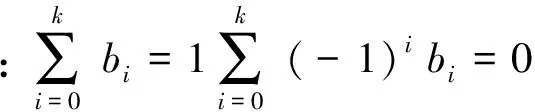
图1 窗函数及其归一化对数频谱Fig.1 Windows and normalized logarithm spectrum

一般而言，窗函数的旁瓣峰值电平和渐进衰减速率对提高谐波信号的检测精度起着至关重要的作用[10-11]为了抑制频谱的泄漏往往需要旁瓣电平低的窗函数.由图1可知，8项余弦窗的主瓣宽度比其他余弦窗宽(12π/N),但是其旁瓣峰值电平最低且旁瓣衰减速率最快.因此本文选用8项余弦窗对信号进行加权处理.

表1 窗函数系数表
Tab.1 Parameters of window coefficients

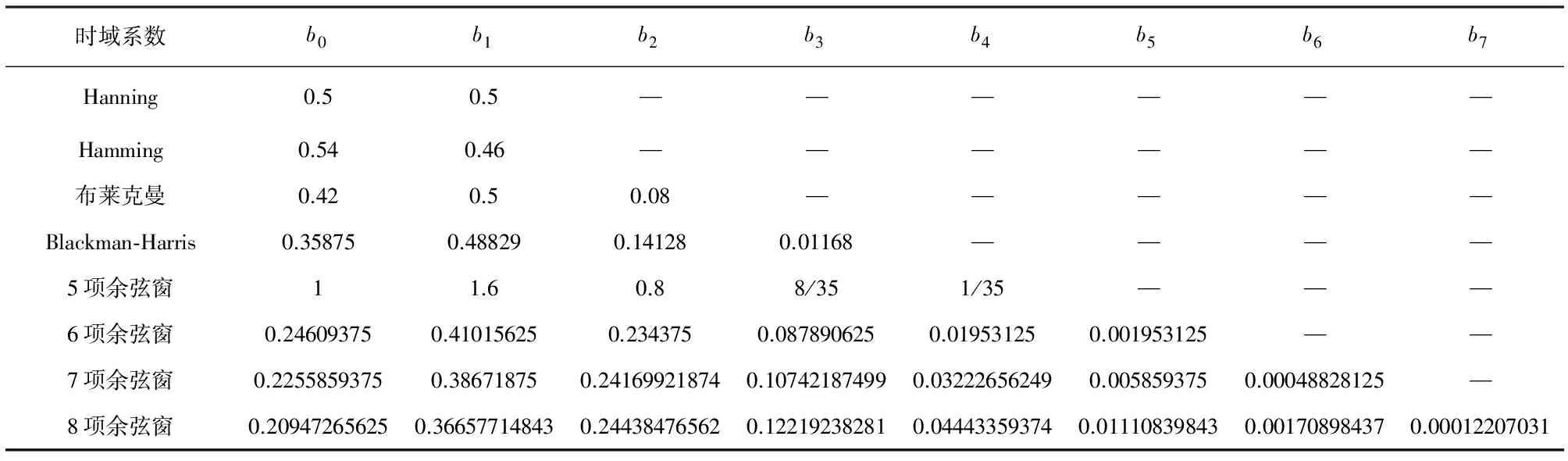
时域系数b0b1b2b3b4b5b6b7Hanning0．50．5——————Hamming0．540．46——————布莱克曼0．420．50．08—————Blackman⁃Harris0．358750．488290．141280．01168————5项余弦窗11．60．88/351/35———6项余弦窗0．246093750．410156250．2343750．0878906250．019531250．001953125——7项余弦窗0．22558593750．386718750．241699218740．107421874990．032226562490．0058593750．00048828125—8项余弦窗0．209472656250．366577148430．244384765620．122192382810．044433593740．011108398430．001708984370．00012207031

2 四谱线插值算法的原理

以fs为采样频率对含有多次谐波的信号进行N点采样，得到离散信号的表达式为

(2)

式中：h表示谐波次数，Ah、fh、φh表示h次谐波的幅值、频率、相位.对离散信号加窗处理，即xw(n)=x(n)w(n)，并进行傅里叶变换，得

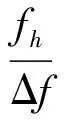
(3)

忽略负频点峰值的旁瓣影响得

(k=0,1,...,N-1)

(4)

式中，W(k)为相应窗函数离散傅里叶变换，可以表示为

(5)

当N>>1时，可以表示为

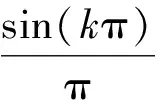
(6)

对第h次的谐波参数进行分析，而忽略其次谐波对第h次谐波的影响，得到相应的谱线表达式为

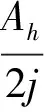
(7)

在信号检测过程中，由于非同步采样的影响，检测第h次谐波的频率khΔf很难落到离散谱线的整数频点上.设第h次谐波的准确频点kh附近的四条谱线分别为kh1、kh2、kh3、kh4、kh2、kh3两条谱线蕴含了第h次谐波的幅值信息量最大，其次是kh1、kh4两两条谱线也蕴含着第h次谐波有用信息，且有kh1=kh2-1，kh2=kh3-1,kh3=kh4-1,δ=kh-kh2-0.5，-0.5≤δ≤0.5.充分利用频点左右四条谱线[12-14]的对称性，获得实际信号参数.令这四条谱线的幅值分别为y1=│X(kh1)│、y2=│X(kh2)│、y3=│X(kh3)│、y4=│X(kh4)│.

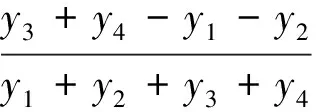
(8)

将式(7)带入式(8)，化简可得：

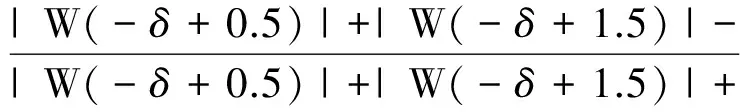
(9)

则可以得到α与δ之间的函数关系α=h(δ)，在[-0.5,0.5]内取一组数δ，求得与之对应的α，且δ由逼近多项式的奇数项构成，可知α与β呈奇函数关系.利用MATLAB中的polyfit(α，δ，7)函数进行多项式拟合δ=h-1(α).由此可得，第h次的信号频率修正公式为

fh=khΔf=(kh2+δ+0.5)

(10)

由于kh2、kh3两条谱线包含大量的幅值信息，所以在谐波幅值计算时应该给这两条谱线更大的加权值，四条谱线的加权值分别为1、2.5、2.5、1.则幅值的估计公式为

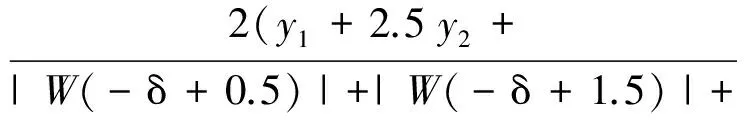
(11)

令

g(δ)= 2/[|W(-β+0.5)|+|W(-β+1.5)|+

|W(-β-1.5)|+|W(-β-0.5)|

(12)

同理，将式(6)带入式(12)中，在[-0.5,0.5]内取一组数δ，求出与之对应的g(δ)，把获得的数据利用polyfit(δ，g(δ)，6)函数进行曲线拟合[15-17].由此得到幅值修正公式为

Ah=2N-1(y1+2.5y2+

2.5y3+y4)g(δ)

(13)

由式(7)可知，相位的修正公式为

arg[(W(-δ-0.5)]

(14)

当N>>1时，arg[W(-K)]=πK.那么相位的修正公式为

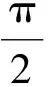
(15)

各种窗函数的修正公式

本文对δ进行多项式拟合时拟合次数取7次,幅值的数据拟合时采用修正项幂次选为6次.利用MATLAB软件中的polyfit函数拟合得到对应的窗函数修正公式.窗函数修正公式为：

(1) Hanning窗函数

δ=0.083506670343413α7+

0.099217837866653α5+

0.219943541561816α3+

0.937496738556471α

U=0.003153822600128δ6+

0.022229168004020δ4+

0.121623658436418δ2+

0.368155385160077

(2) Hamming窗函数

δ=0.100496085398161α7+

0.101897443601928α5+

0.217846619862153α3+

0.851218993653637α

U=0.003486364666952δ6+

0.023749847515743δ4+

0.124900735560296δ2+

0.360936651511512

(3) Blackman窗函数

δ=0.129901255735445α7+

0.161476128964892α5+

0.317503828311633α3+

1.208943283350772α

U=0.001943321525962δ6+

0.017233120172110δ4+

0.113890627291849δ2+

0.405202470388241

(4) Blackman-Harris窗函数

δ=0.191153143824769α7+

0.240737867783245α5

+0.435285503533033α3+

1.547158446062135α

U=0.001181004084057δ6+

0.013134789931189δ4+

0.105236495920637δ2+

0.443778779151877

(5) 5项余弦窗

δ=0.197279974426130α7+

0.302988042173697α5+

0.612564490124994α3+

2.474999995459783α

U=1.335654659178952×10-4δ6+

0.002119650787261δ4+

0.024167588490127δ2+

0.145338687467616

(6) 6项余弦窗

δ=0.236006162444184α7+

0.367108650653804α5+

0.739620297143259α3+

2.979166665411265α

U=3.254090617978365×10-4δ6+

0.006132203426704δ4+

0.082120830995647δ2+

0.575818038105339

(7) 7项余弦窗

δ=0.274831341030455α7+

0.430754070955065α5+

0.866094571629454α3+

3.482142856531179α

U=2.293750007995112e×10-4δ6+

0.005006315270912δ4+

0.077018630321852δ2+

0.616947898039491

(8) 8项余弦窗

δ=0.313717189979371α7+

0.494107524257485α5+

0.992202948039989α3+

3.984374999634126α

U=1.687424914138081×10-4δ6+

0.004186748276859δ4+

0.072759525148811δ2+

0.655507141710313

3 信号的仿真实验分析

表2 基波及谐波信号的幅值及相位
Tab.2 The amplitude and phase of the fundamental wave and harmonic signal

谐波次数123456789幅值/V3802060153020171610相位/(°)1501209060304020105

为了验证提出的算法的有效性，本文仿真所用的基波及谐波的幅值及相位，见表2.采用的基波频率为50.1Hz，采样频率为5120Hz，采样点数为1024点.本文利用MATLAB软件对含有不同频率的电网谐波信号进行加不同窗函数的算法仿真.加不同余弦窗插值FFT算法的幅值、相位的仿真测量结果分别见表3和表4，不同加窗插值算法的幅值及相位相对误差的仿真结果分别见表5和表6.

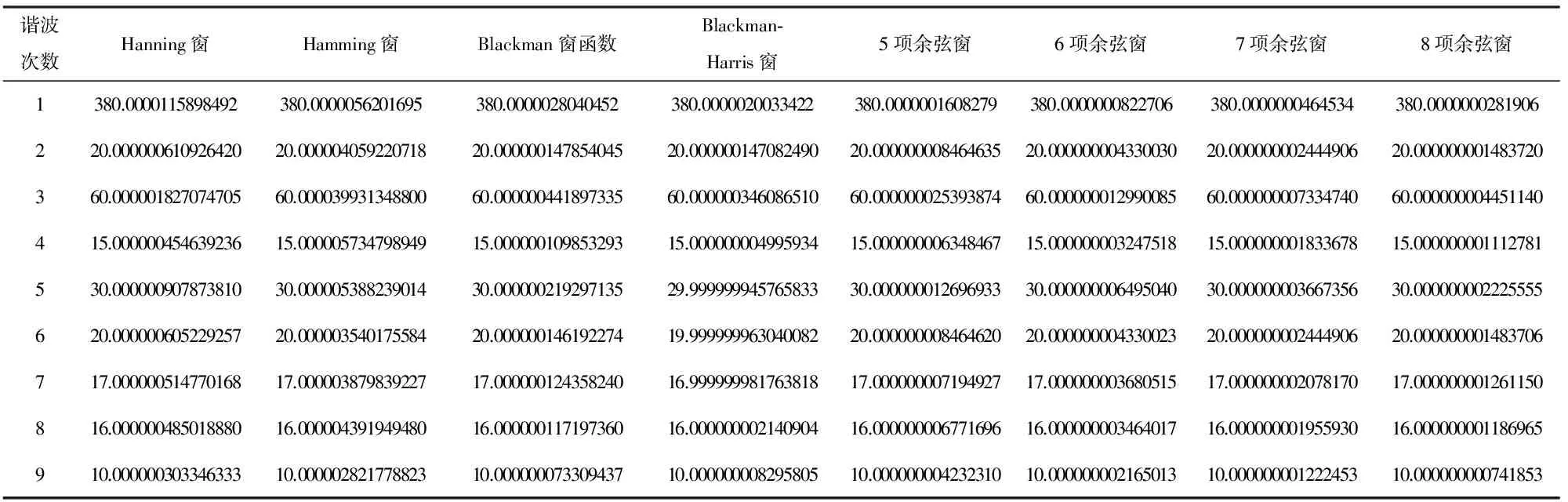
表3 不同加窗插值FFT算法的幅值的测量结果
Tab.3 Amplitude of measured results corresponding to different window interpolation FFT algorithms

谐波次数Hanning窗Hamming窗Blackman窗函数Blackman⁃Harris窗5项余弦窗6项余弦窗7项余弦窗8项余弦窗1380．0000115898492380．0000056201695380．0000028040452380．0000020033422380．0000001608279380．0000000822706380．0000000464534380．0000000281906220．00000061092642020．00000405922071820．00000014785404520．00000014708249020．00000000846463520．00000000433003020．00000000244490620．000000001483720360．00000182707470560．00003993134880060．00000044189733560．00000034608651060．00000002539387460．00000001299008560．00000000733474060．000000004451140415．00000045463923615．00000573479894915．00000010985329315．00000000499593415．00000000634846715．00000000324751815．00000000183367815．000000001112781530．00000090787381030．00000538823901430．00000021929713529．99999994576583330．00000001269693330．00000000649504030．00000000366735630．000000002225555620．00000060522925720．00000354017558420．00000014619227419．99999996304008220．00000000846462020．00000000433002320．00000000244490620．000000001483706717．00000051477016817．00000387983922717．00000012435824016．99999998176381817．00000000719492717．00000000368051517．00000000207817017．000000001261150816．00000048501888016．00000439194948016．00000011719736016．00000000214090416．00000000677169616．00000000346401716．00000000195593016．000000001186965910．00000030334633310．00000282177882310．00000007330943710．00000000829580510．00000000423231010．00000000216501310．00000000122245310．000000000741853

表4 不同加窗插值FFT算法的相位的测量结果
Tab.4 Phase of measured results corresponding to different window interpolation FFT algorithms

谐波次数Hanning窗函数Hamming窗函数Blackman窗函数Blackman⁃Harris窗函数5项余弦窗函数6项余弦窗函数7项余弦窗函数8项余弦窗函数1150．0000185893350150．0047781706550150．0000009522580149．9995643713359150．0000000153427150．0000000035204150．0000000010162150．00000000034782120．0000325598955119．9811590830788120．0000068525453120．0017218505611120．0000000153424120．0000000035203120．0000000010227120．0000000003478390．00004349365656089．96905390813967090．00001148461948090．00282322846435090．00000001534254090．00000000352028090．00000000102600090．000000000347700460．00004045690534659．98077391511049060．00001021640926560．00176728777829060．00000001534293060．00000000352068060．00000000102315060．000000000348130530．00002648636847330．00437865851673530．00000431612241429．99960966903164230．00000001534294530．00000000352074330．00000000101649230．000000000347956640．00003158725359039．99667910125114040．00000647238196040．00031695520855040．00000001534231040．00000000352009040．00000000101817040．000000000347484720．00002175175588820．01066295846106020．00000231282711719．99902976134120020．00000001534323220．00000000352097720．00000000101489320．000000000348140810．00001795448168010．01479057152726410．0000007041226029．99864719719642610．00000001534236710．00000000352016910．00000000101298910．00000000034753595．0000165565279755．0158827515515425．0000001109301794．9985454477174325．0000000153422335．0000000035200735．0000000010126645．000000000347527

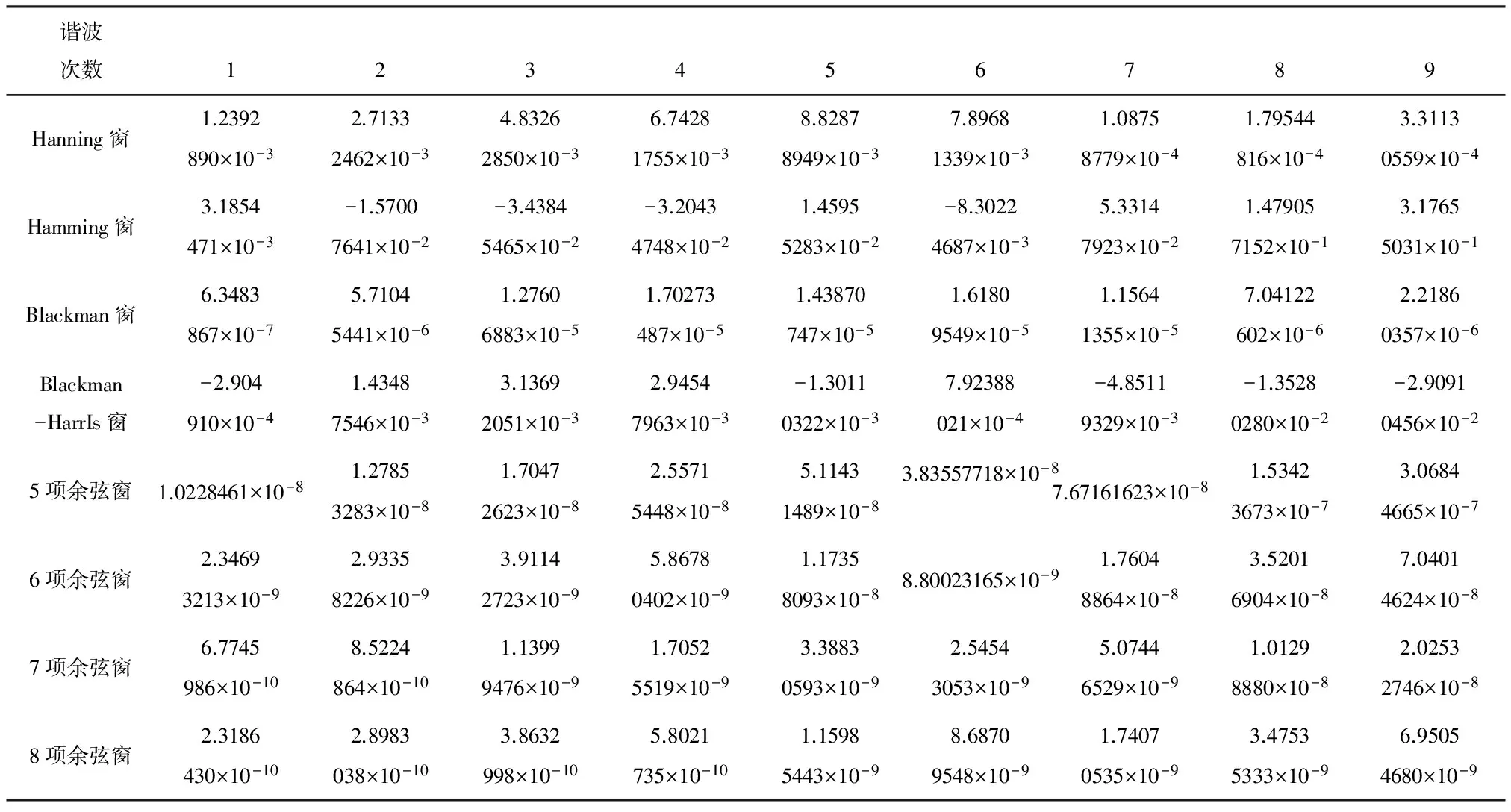
通过仿真，由表3至表6可知，加8项余弦窗算法得到的频率、幅值、相位结果比加其他窗函数得到的结果精度高.加8项余弦窗的算法与加7项余弦窗的算法相比，加8项余弦窗的加窗插值算法的幅值精度比加7项余弦窗算法精度提高了1个数量级；对于相位精度而言，加8项余弦窗插值算法的精度比加7项的算法精度提高了1个数量级.加8项余弦窗的算法与加6项余弦窗的算法相比，加8项余弦窗的加窗插值算法的幅值精度比加6项余弦窗的算法的精度提高了1个数量级；对于相位精度而言，加8项余弦窗插值算法的精度比加6项的检测精度高.加8项余弦窗的算法与加5项余弦窗的算法相比，加8项余弦窗的加窗插值算法的幅值精度比加5项余弦窗的算法提高了2个数量级；对于相位精度而言，加8项余弦窗插值算法的精度比加5项余弦窗算法的精度提高了2个数量级.加8项余弦窗的算法与加Hanning窗、Hamming窗、Blackman窗、Blackman-Harris窗的算法相比，加8项余弦窗的加窗插值算法的幅值精度比加这些余弦窗的算法精度至少提高了3个数量级；对于相位精度而言，加8项余弦窗插值算法的精度比加Hanning窗、Hamming窗、Blackman窗、Blackman-Harris窗检测精度至少提高了3个数量级.这表明加8项余弦窗插值算法能够有效地减小栅栏效应带来的电网谐波检测的误差，提高信号参数(频率 幅值 相位)的检测精度，适于电网谐波高精度检测.

4 结束语

本文通过分析不同余弦窗函数的旁瓣特性，结合四谱线插值算法对电网谐波进行了分析处理，导出了加8项余弦窗的四谱线插值的频率、相位、幅值的修正公式.本文利用MATLAB软件进行仿真，并与加其他窗函数的算法相对比，采用本文算法得到的谐波信号参数的结果的精度更高而且计算量小，具有较快的计算速度.

表5 不同加窗插值算法的幅值相对误差比较
Tab.5 Relative errors comparison of amplitude using different window interpolation algorithms

谐波次数123456789Hanning窗1．85893350×10-33．25598955×10-34．34936565×10-34．04569053×10-32．64863684×10-33．15872535×10-32．17517558×10-31．79544816×10-31．65565279×10-3Hamming窗4．77817065×10-1-1．88409169-3．09460918-1．92260844．37865851-3．320898741．066295841．479057151．58827515Blackman窗9．52258005×10-56．85254529×10-41．14846194×10-51．02164092×10-34．31612241×10-46．47238196×10-42．31282711×10-47．04122602×10-51．10930178×10-5Blackman-HarrIs-4．35628664×10-21．72185056×10-12．82322846×10-11．76728777×10-1-3．90330968×10-23．16955208×10-2-9．70238658×10-2-1．35280280×10-1-1．45455228×10-15项余弦窗1．53426924×10-61．53423940×10-61．53425361×10-61．53429269×10-61．53429446×10-61．53423087×10-61．53432324×10-61．53423673×10-61．53422332×10-66项余弦窗3．52039819×10-73．52029871×10-73．52028450×10-73．52068241×10-73．52074280×10-73．52009266×10-73．52097728×10-73．52016904×10-73．52007312×10-77项余弦窗1．01618979×10-71．02269837×10-71．02599528×10-71．02315311×10-71．01649177×10-71．01817221×10-71．01489305×10-71．01298880×10-71．01266373×10-78项余弦窗3．47796458×10-83．47796458×10-83．47696982×10-83．48130413×10-83．47956330×10-83．47483819×10-83．48141071×10-83．47535333×10-83．47527340×10-8

表6 不同加窗插值算法的相位相对误差比较
Tab.6 Relative errors comparison of phase using different window interpolation algorithms

谐波次数123456789Hanning窗1．2392890×10-32．71332462×10-34．83262850×10-36．74281755×10-38．82878949×10-37．89681339×10-31．08758779×10-41．79544816×10-43．31130559×10-4Hamming窗3．1854471×10-3-1．57007641×10-2-3．43845465×10-2-3．20434748×10-21．45955283×10-2-8．30224687×10-35．33147923×10-21．479057152×10-13．17655031×10-1Blackman窗6．3483867×10-75．71045441×10-61．27606883×10-51．70273487×10-51．43870747×10-51．61809549×10-51．15641355×10-57．04122602×10-62．21860357×10-6Blackman-HarrIs窗-2．904910×10-41．43487546×10-33．13692051×10-32．94547963×10-3-1．30110322×10-37．92388021×10-4-4．85119329×10-3-1．35280280×10-2-2．90910456×10-25项余弦窗1．0228461×10-81．27853283×10-81．70472623×10-82．55715448×10-85．11431489×10-83．83557718×10-87．67161623×10-81．53423673×10-73．06844665×10-76项余弦窗2．34693213×10-92．93358226×10-93．91142723×10-95．86780402×10-91．17358093×10-88．80023165×10-91．76048864×10-83．52016904×10-87．04014624×10-87项余弦窗6．7745986×10-108．5224864×10-101．13999476×10-91．70525519×10-93．38830593×10-92．54543053×10-95．07446529×10-91．01298880×10-82．02532746×10-88项余弦窗2．3186430×10-102．8983038×10-103．8632998×10-105．8021735×10-101．15985443×10-98．68709548×10-91．74070535×10-93．47535333×10-96．95054680×10-9

[1]杨帆,李晓明,郑秀玉.电力系统分数次谐波的产生机理、危害与特征[J].高电压技术, 2007, 33(12): 153-156.

[2]温和, 腾召胜,王永,等. 改进加窗插值 FFT 动态谐波分析算法及应用[J].电工技术学报, 2012, 27(12): 270-273.

[3]彭祥华,周群,曹晓燕.一种高精度的电网谐波/间谐波检测的组合优化算法[J].电力系统保护与控制, 2014, 42(23): 95-101.

[4〗郝柱,顾伟,褚建新,等.基于四谱线插值 FFT 的电网谐波检测方法[J].电力系统保护与控制,2014,42(19): 107-112.

[5]张伏生 ,耿中行, 葛耀中.电力系统谐波分析的高精度 FFT 算法[J].中国电机工程学报,1999,19(3)：63-66.

[6]许珉,张鸿博. 基于Blackman-harris窗的加窗 FFT插值修正算法[J].郑州大学学报(工学版),2005,26(4): 99-101.

[7]周俊,王小海，祁才君. 基于Blackman窗函数的插值FFT在电网谐波信号分析中的应用[J.浙江大学学报(理学版)，2006，33(6)：650-653.

[8]丁文浩,袁志民. Hanning窗在插值FFT算法中应用的研究[J]. 电测与仪表, 2008, 45(12): 15-19.

[9]熊杰锋,王柏林,孙艳.电力系统间谐波和谐波分析的海宁窗插值算法[J]．自动化仪表，2010，31(4)：25-26，33．

[10]李绍铭,纪萍,彭玉龙.基于加窗插值 FFT 和动态频率的谐波检测算法[J].自动化与仪器仪表,2009(3): 93-95.

[11]黄纯,江亚群.谐波分析的加窗插值改进算法[J]．中国电机工程学报，2005，25(15)：26-31．

[12]罗蛟,江亚群,黄纯,等. 基于DRSC窗递推DFT算法的电力谐波检测[J]. 电工技术学报, 2013, 28(9): 47-53.

[13]薛蕙,杨仁刚.基于FFT的高精度谐波检测算法[J].中国电机工程学报, 2002,22(12): 106-110.

[14]牛胜锁,梁志瑞,张建华,等.基于三谱线插值 FFT 的电力谐波分析算法[J].中国电机工程学报,2012, 32(16): 130-136.

[15]CHANG G,LIU L . Measuring power system harmonic and interharmonics by an improved fast fourier transform-based algorithm [J]. IET Gener. Transm. Distrib. 2008, 2(2):192-201

[16]肖先勇, 王楠, 刘亚梅.基于多项式逼近的单峰谱线插值算法在间谐波分析中的应用[J]. 电网技术, 2008,32(18): 57-61.

[17]罗蛟, 江亚群, 黄纯, 等. 基于DRSC窗递推DFT算法的电力谐波检测[J]. 电工 技术学报, 2013, 28(9): 47-53.