空降夺岛作战战场抢修保障组优化方法*

杨建文，石文华，姜为学

（空军空降兵学院，广西 桂林 541003）

0 引言

当前，岛屿夺控是我军军事演习和训练的重要科目，空降夺岛作战也成为近几年的研究热点。空降夺岛作战环境险恶，参战装备会出现大量损伤。为了满足战场抢修的需要，迫切要求在空降空投阶段空投尽可能多的抢修力量。然而，若配置过多的抢修力量，会增大空投负担甚至超过空投能力限制，并且可能造成抢修资源的闲置浪费；反之，如果抢修力量配置过少，就可能导致装备的战场损伤不能及时得到抢修，影响其战斗力发挥，延误作战进程和错失有利战机。因此，配置合适的抢修力量成为满足空投能力限制要求和战场抢修需求的关键，对空降夺岛作战有重要的现实指导意义。

排队论是解决抢修装备数量需求问题的有效方法［1］。文献［2］用排队理论分析了维修保障过程，给出了平均维修等待时间计算公式，但没有给出故障发生率的计算方法。文献［3］参考军方研究成果分析航线维修人员构成的随机服务系统特征，利用M/M/C多个服务台和无限排队规则的排队论方法，通过建立约束条件进行实例分析，结果科学直观地验证了方案的合理性。文献［4］把战场维修看作排队系统，建立了装备维修小组数量优化模型。

这些研究成果利用排队论解决问题时，系统顾客到达率都是根据经验数据直接给出，且服务时间都认为是服从指数分布。这并不完全适用于空降夺岛作战战场抢修，因为空降夺岛作战的装备故障规律需要考虑到作战对抗，且并不是所有专业抢修时间都服从指数分布。针对上述问题，本文利用兰彻斯特方程计算战场损伤强度，根据排队论推导损伤修复等候时间的计算公式，并根据战场抢修等候的时效性要求计算不同专业需要配备的抢修单元小组最佳数量。

1 空降夺岛作战战场抢修分析

以空降兵为作战主体的空降夺岛作战具有“走在空中、打在地面、保障在远方”的特点［5］，险恶的作战环境决定了其战场抢修具有战场抢修力量规模受限、支援难度大、时效要求高、抢修专业杂的特点。

空降夺岛作战战场抢修的特点决定了机动保障是其作战装备战场抢修的最佳方式，即把空投后的战场抢修力量按照专业均匀编组为若干个单元小组，每个单元小组配备一定数量的人员，以空投型抢修车为行走工具，携带不同专业抢修设备和备件器材，根据战场抢修需要，赶赴损伤现场进行现地抢修［5］，完成任务后，再迅速撤收并转而抢修其他出现损伤的装备。

在空降夺岛作战中，装备出现损伤的时间是随机的，所需的抢修时间也是随机的，因此，战场抢修可以看作为随机服务系统。把损伤装备看作需要服务的顾客，战场损伤从出现到抢修力量赶来修复所经过的时间就是顾客的排队等候时间T'，可利用排队论得出其计算公式。

2 模型构建

2.1 目标函数确定

空降夺岛作战的战场抢修单元小组数量确定主要基于以下考虑：

（1）战场抢修力量若配置过少，可能出现等待抢修的损伤装备构成的队列无限长的情形，导致部分损伤得不到抢修，就是排队论所要求的服务强度ρ 不能大于 1，即 ρ≤1。

设ρ=1时的抢修单元小组数为c1。

（2）出现战场损伤后，要求抢修力量必须在规定时间T*内到达现场进行抢修，也就是说，战场损伤从出现到抢修力量赶来修复所等候的平均时间T'不得超过T*，记为T'≤T*。设满足此需求的抢修单元小组数为c2。

综上所述，战场抢修需要配置的最佳抢修单元小组数c为

式（1）的意义在于，为空降夺岛作战配置的抢修单元小组数首先不会导致等候抢修的损伤装备队列无限长，然后又满足作战规定的时效性要求。配置数量若小于c，则可能导致等候抢修的损伤装备队列无限长，或不满足时效性要求；配置数量若大于c，则会增大作战准备阶段的空投负担，也可能导致抢修资源的闲置浪费。

已知参加空降夺岛作战的某型装备数量为m，配置的抢修单元小组数为c。对于维修时间服从指数分布的损伤，其抢修可以看作有限顾客源情形下的多服务台排队系统，记作；对于维修时间不服从指数分布，比如服从正态分布的损伤，其抢修可以看作有限顾客源情形下的多服务台排队系统，记作。

为计算空降夺岛作战战场抢修单元小组最佳数量，下面给出T'的计算公式。

2.2 条件假设

为了建模需要，给出如下假设条件：

①敌我双方指挥员均不犯明显错误，且参战装备可以实现体系对抗；

②战场上双方的战斗力损失规律用指数分布描述，战场抢修系统的输入过程，即战场损伤的出现是泊松流［6］；

③机械损伤的维修时间服从正态分布，电子系统损伤的维修时间服从指数分布［8］；

④空降夺岛作战战场抢修采用机动保障方式，且抢修力量自始至终未遭到敌方袭击；

⑤战场抢修力量只能完成对轻度战损装备的修理任务，即只具备小修能力，且修复损伤时备件充足；

⑥由使用人员可以运用随车工具在短时间内修复的损伤忽略不计。

2.3 指数型抢修时间情形下的等候时间

其中，Ls为等待修复的和正在进行修复的装备数量。

已知平均修复率（服务率）为μ，则服务强度ρ为：

经过推导，有n个装备出现损伤的稳态概率Pn为：

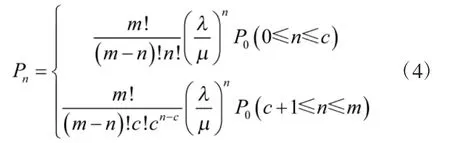
其中，P0为所有抢修力量整体处于空闲的概率，表示为

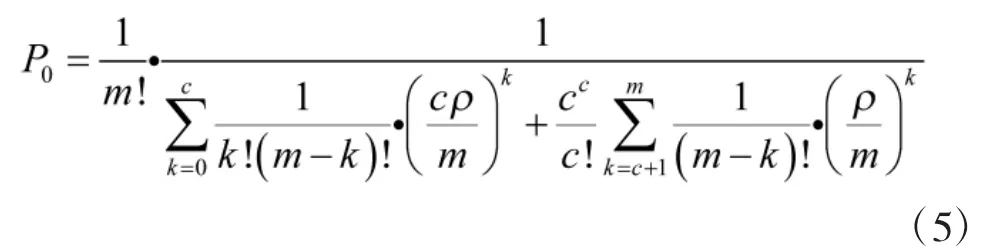
则平均故障装备数为

除去正在抢修的装备，等待进行抢修的装备数量为

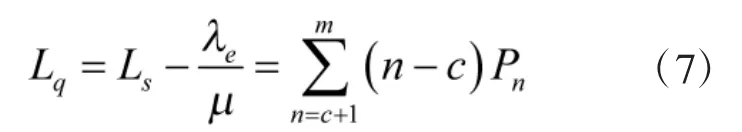
根据Little公式［8］得到战场损伤得到抢修的平均等候时间T'为

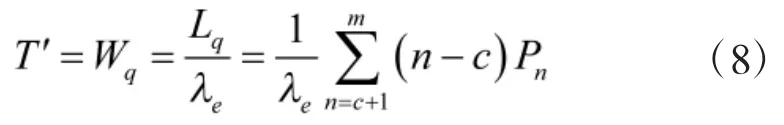
2.4 一般型抢修时间情形下的等候时间

对于战场损伤抢修时间T'不服从指数分布的情形，已知其期望值为E［T］，方差为Var［T］，则

计算 Ls的 P-K 公式［8］为

则根据Little公式得到T'为

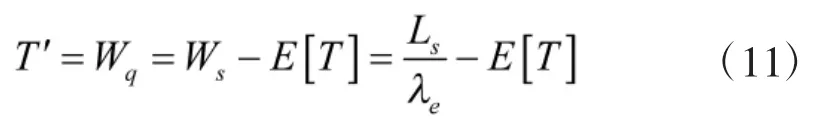
2.5 综合损伤强度计算

受击损伤和技术损伤是因为两个有本质区别的原因导致，可以假设其为两个独立事件，则装备的综合损伤强度为

技术损坏强度就是装备故障率，可以由平时使用过程中的统计数据得到。下面给出受击损坏强度的计算方法。

2.5.1 受击损伤强度计算

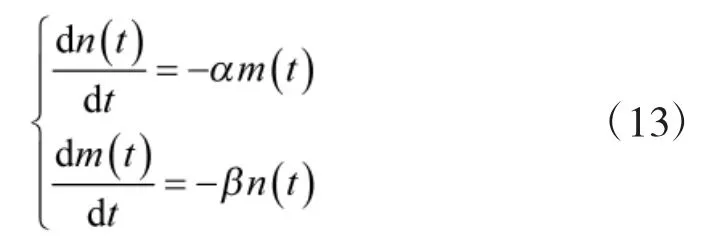
式中，t为战斗时刻；m（t）和 n（t）为 t时刻蓝方、红方在战斗中剩存的战斗单位数量；α、β分别为战斗力系数。

文献［10］指出，装备的战损量影响因素包括作战类型与样式，兵力、兵器数量和质量、自然环境、作战持续时间、人，等等。对于空降夺岛作战而言，作战类型与样式和自然环境是基本确定的因素，兵力、兵器数量和质量及作战持续时间成为关键因素，尤其是参战装备的毁伤能力至关重要。此时，描述空降夺岛作战的兰彻斯特方程模型运行的关键就是确定对抗双方的综合毁伤能力。参战双方一般都有多个不同类型、不同级别、使用不同武器的战斗单位，对抗双方的综合毁伤能力，主要用对单件装备火力毁伤指数求和得出的综合值来衡量，而单件装备的火力毁伤指数，也就是战斗力主要是根据历次战争和演习总结得出的。

已知在空降夺岛作战中，敌我双方参战部队的初始战斗力分别为M1和M2，假设我方战斗力大于敌方战斗力，如果使敌方损失达到S终，则根据兰彻斯特方程可以得到战斗结束时我方战斗力损失率为

若是敌方战斗力大于己方战斗力，则战斗终止时我方损失率用可接受的损失率确定为

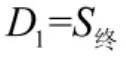
因为已经假设战场上双方的战斗力损失规律服从指数分布，则战斗力损失强度为

以上表示的是整个作战部队的装备受击损坏强度，为了表征不同类型装备的损坏强度，引入受击损坏区分系数 γ［6］。

设我方共有J1种武器装备，已知武器j的受击损坏区分系数为γj，编配数量为C1j，等效作战价值为vj，则在作战时间T内，武器j的受击损坏强度为

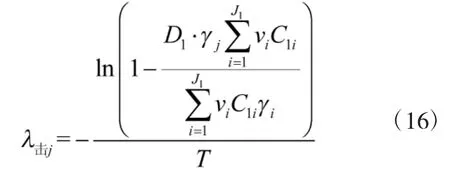
2.5.2 综合损伤强度计算

根据假设条件5，空投到战场的抢修力量只对轻损具备修复能力，中损和重损留作战后处理。因此，并不是出现的所有损伤都可以立即进行抢修。文献［7］给出了在出现的战场损伤中，计算装备轻损、中损和重损的比例的计算模型，且得出轻损比例 α1为

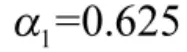
装备（或装备某个专业系统）j的综合损伤强度为

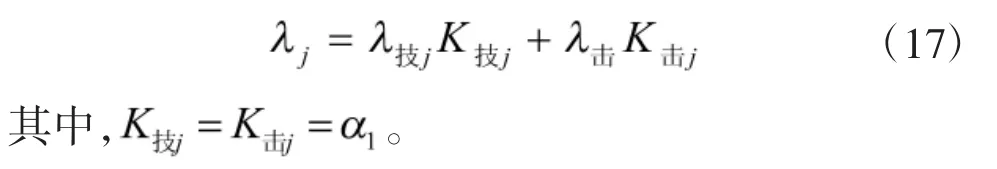
3 实例应用

空降机械化部队是进行岛屿夺控的重要力量，某型伞兵战斗车是空降机械化部队的主战装备，本文以其为例研究战场抢修保障力量编组。

3.1 战场损伤强度计算

首先给出作战想定。已知我方岛屿A被蓝军非法占领，通过情报侦察，得知蓝军部署了一个机步旅守卫岛屿A。我方决定以空降兵为作战主体进行空降夺岛作战，夺得岛屿A的控制权。已知在作战过程中，我方会得到8架某型轰炸机的支援，计划在27 h内击溃该蓝军机步旅［5］。

我方和蓝方在空降夺岛作战中投入的主要武器装备及各类装备的等效战斗价值如表1所示。

已知我方的战斗素质指数e素为1.1，态势指数e态和地形指数e地均为1；蓝军的战斗素质指数为1.1，岛屿地面崎岖不平，态势指数为1.3，地形指数为1.5。

我方的战斗力计算为

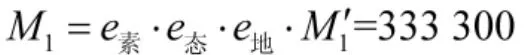
蓝方战斗力为

当敌方兵力损失超过2/3，而我方仍据有兵力优势时，战斗就可以认为结束［6］。因此，击溃蓝方坚固防御体系的损失率定为0.7，也就是说，当蓝方战斗力损失达到0.7时，其防御体系将基本崩溃。

此时，把上述数据代入式（14），计算得到我方兵力损失率约为

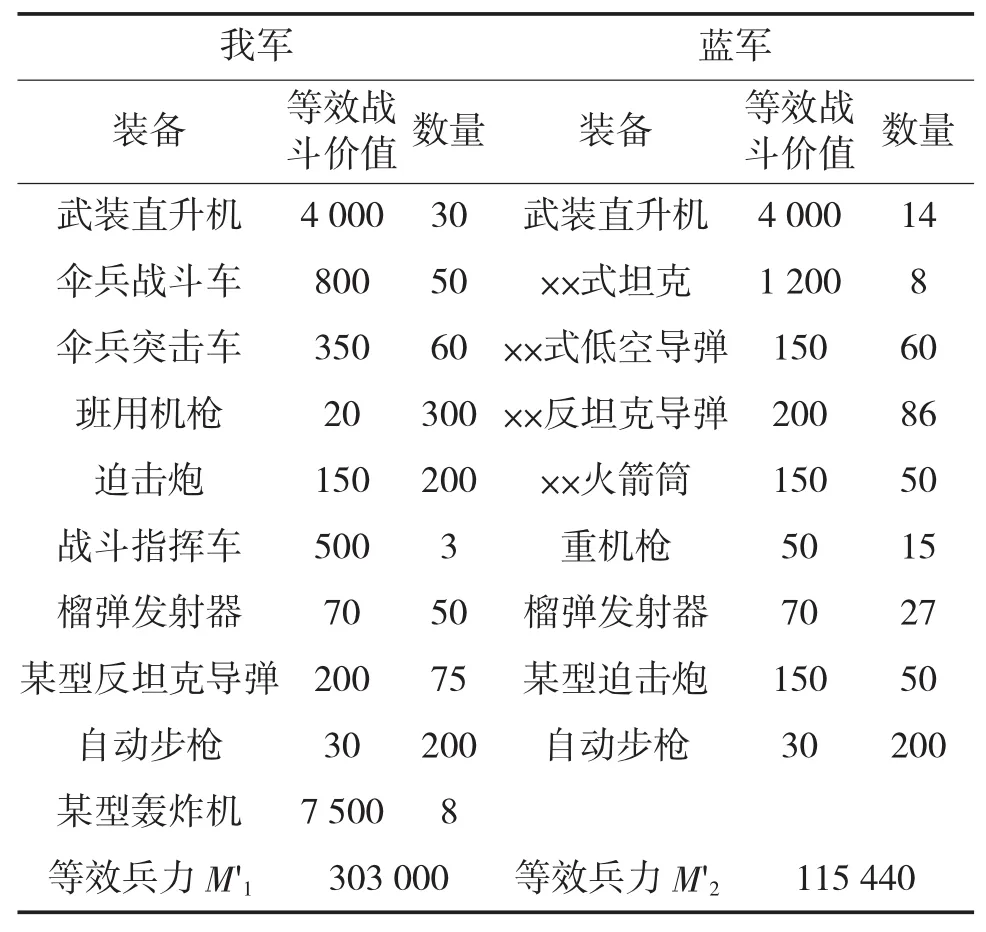
表1 我方与敌方武器装备及战斗力列表

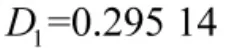
已知作战计划为27 h，把D1的值代入式（15），得到装备的平均受击损坏强度为

对于伞兵战斗车，已知其受击损坏区分系数为γ=3.6，文献［6］给出了各类武器装备的受击损坏区分因子，根据式（16）得到伞兵战斗车的受击损坏强度为

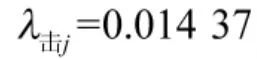
伞兵战斗车的损伤的抢修主要涉及到3个专业：通信指挥系统专业、底盘专业、军械（武器系统）专业，分别用 j=1，j=2，j=3 表示。

已知不同专业系统的技术损伤强度的统计平均值为

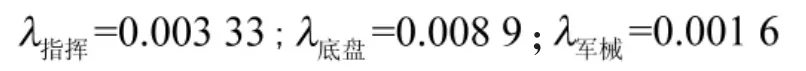
根据式（17）得到综合损伤强度为

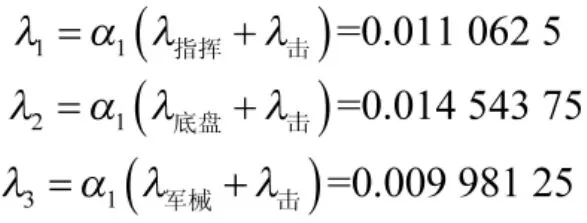
3.2 最佳抢修单元小组数计算

3.2.1 抢修时间为指数分布时的最佳抢修小组数

通信指挥专业的损伤修复时间服从参数为μ=0.251 9指数分布。

根据式（6）计算得到

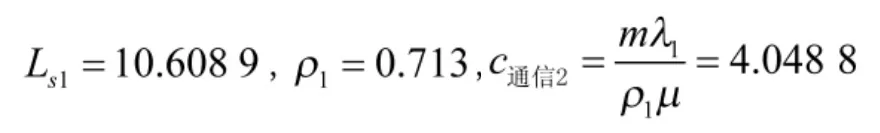
根据 ρ1≤1，当 ρ1=1 时得到 c通信1=1.73。

向上取整，得到通信指挥设备抢修保障小组的最佳数量为5。

3.2.2 抢修时间为非指数分布时的最佳抢修小组数

已知底盘和军械专业的损伤修复时间服从正态分布，其参数分别为 E［T2］=6.87，Var［T2］=0.15；E［T3］=5.3，Var［T3］=0.24。

对于底盘专业损伤的抢修，令T'=0.5，根据式（11）计算得到等待抢修和正在抢修的装备数为Ls2=4.84，代入式（10），得

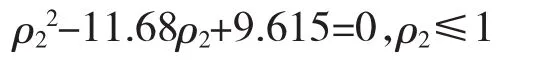
得到 ρ2=0.891 2。

根据式（9），得到

已知 ρ2≤1，当 ρ2=1 时得到 c底盘1=4.512。

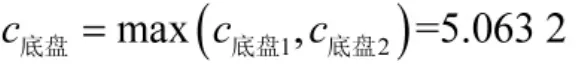
向上取整，得到底盘专业抢修保障小组的最佳数量为6。

c底盘取不同的数值，对应的Ls2和T'是不同的，其变化趋势如表2所示。

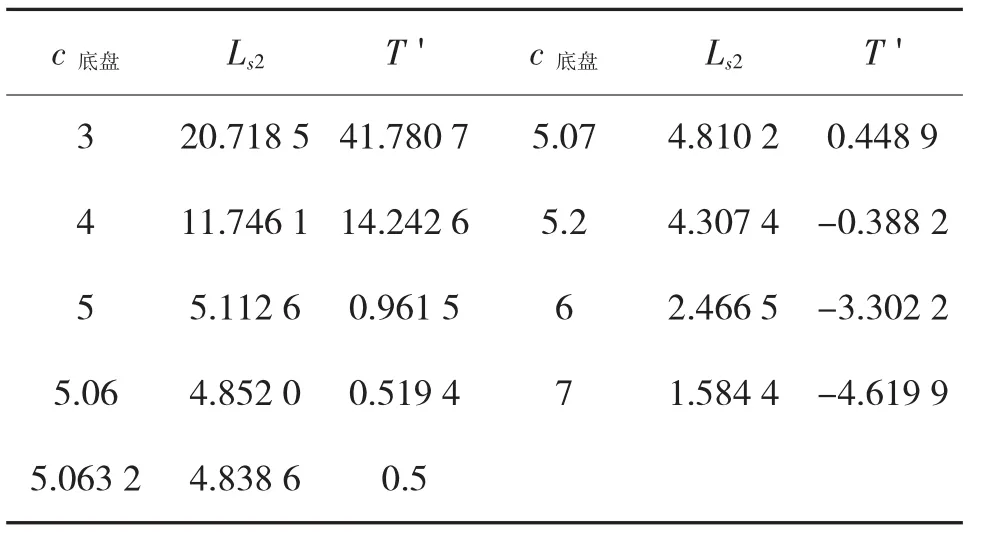
表2 c底盘取不同数值时的等候时间

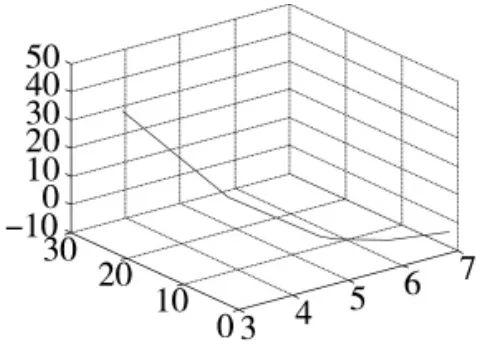
图 1 c底盘、Ls2和 T'之间的关系图

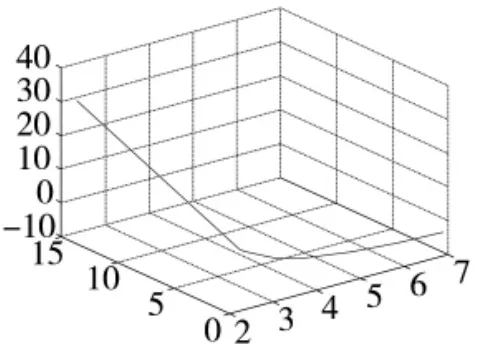
图 2 c军械、Ls3和 T'之间的关系图

根据表2得到c底盘、Ls2和T'之间的关系图如图1所示。

由图1可见，随着c底盘的增大，Ls2和T'在不断变小。

对于军械专业损伤的抢修，令T'=0.5，得到Ls3=2.736。

代入式（10），得到 ρ3=0.814。

根据式（9），得到

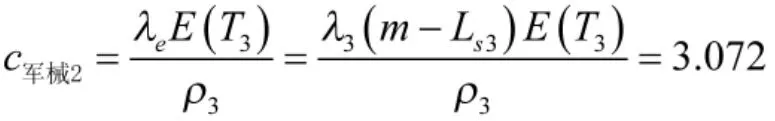
已知 ρ3≤1，当 ρ3=1 时得到 c军械1=2.5。

向上取整，得到军械专业抢修保障小组的最佳数量为4。

同样，c军械取不同的数值，对应的Ls3和T'是不同的。c军械、Ls3和T'之间的关系如图2所示。

4 结论

本文通过分析空降夺岛作战战场抢修的特点，把其看作排队系统，考虑到不同装备不同专业抢修时间服从不同分布，分别推导了损伤修复等候时间和战场损伤强度的计算公式，并根据战场抢修等候的时效性要求计算了某型伞兵战斗车各个专业需要配备的抢修单元小组数量，为制定空降夺岛作战战场抢修计划提供了定量依据。基于本文方法，运用仿真平台构建空降夺岛作战战场抢修资源优化配置系统是下一步的研究重点。

［1］王正元，朱昱，曹继平.装备维修保障辅助决策方法［M］.北京：国防工业出版社，2014.

［2］刘文武，于永利，任帆.基于随机网络的平均维修保障服务时间分析［J］.项目管理技术，2010，8（11）：57-61.

［3］卿光辉，刘恺铭，李耀华.航线维修MLDT中保障组优化方法研究［J］.中国民航大学学报，2015，33（5）：29-32.

［4］邵延君.武器装备预防性维修理论与方法［M］.北京：电子工业出版社，2015.

［5］海占勇，纪光.空降作战装甲装备保障研究［M］.北京：蓝天出版社，2015.

［6］朱小冬，王毅刚，周辅疆.地面作战装备维修保障系统结构设计理论与方法［M］.北京：国防工业出版社，2015.

［7］石文华，杨建文，姜为学.空降装甲装备战场损伤修理工作量预计建模研究［J］.兵器装备工程学报，2016，37（12）：118-120.

［8］甘应爱，田丰.运筹学［M］.北京：清华大学出版社，2005.

［9］王永娟，王亚平，徐诚.步兵自动武器现代设计理论与方法［M］.北京：国防工业出版社，2014.

［10］陆凡，谢晴.装备战损量的兰彻斯特方程预计方法［J］.指挥控制与仿真，2007，29（3）：100-104.

［11］张仲敏，李俊山，严其飞，等.电子对抗装备维修备件混合分类决策模型［J］.火力与指挥控制，2014，39（4）：58-62.