基于多优化策略RRT的无人机实时航线规划

李俊涛，毛红保，张 鹏，胡京林

（空军工程大学航空航天工程学院，西安 710038）

0 引言

随着战场复杂性的提高，各国的防空网络呈现出高密度的趋势［1］。同时，无人机执行任务的复杂性也急剧增加［2］。因此，传统无人机航线规划因其过度简化的模型和较差的实时性，产生的航线已难以确保无人机的安全［3］。

目前的航线规划算法可以分为两类：基于组合规划思想和基于采样的航线规划算法。基于组合规划的算法主要利用离散化方式构建任务空间模型，通过图论或线性规划等方法解算无人机航线。其典型方法包括 MILP 算法［4］、最优控制法［5］、Voronoi图法［6］以及A*算法［7］。此类算法总能解算出最优解，但其对任务空间信息的完整性需求使得算法的实时规划能力较弱。

基于采样的规划算法避免构建空间整体结构，采用增量方式探测空间中的安全区域形成可行航线。典型的算法包括遗传算法［8］、蚁群算法［9］以及PSO算法［10］等。基于采样的算法解算出的航线优化性相较组合规划方法稍差，但规划解算速度快。

针对目前大多数算法对模型的过度简化和实时性差的问题，提出基于多优化策略快速扩展随机树（Multi-Optimization Rapidly exploring Random Tree，MO-RRT）无人机实时航线规划算法。RRT算法执行效率高，且具备概率完备性，但其随机思想也存在优化不足的缺点。本文提出的MO-RRT算法以标准RRT算法为基础，基于敌方威胁的精确建模，建立基于目标启发的快速收敛航线规划算法。同时，MO-RRT算法也针对航线的平滑性进行优化设计。最终，该算法能够实现威胁环境未知的实时航线规划。

1 标准RRT算法基本原理

标准RRT算法能够根据实时环境信息快速地搜索规划空间，通过组态空间的随机采样点，将搜索导向空白区域，适用于解决航线规划问题［11］。其规划生成过程为：

输入：航线规划起始点N0、目标点Ngoal；

Step1：以航线起始点作为搜索树的根节点Nroot，对搜索树Search-Tree初始化，仅包含根节点；

Step2：在规划区域产生随机点Nrand，在当前搜索树Search-Tree中，遍历所有节点，确定距Nrand最近的节点，定义为Nnear；

Step3：按一定的步长生成新节点Nnew，确定生长路径；

Step4：判断新节点Nnew是否在威胁区域内，若是，则转到Step2；否则，转入Step5；

Step5：判断新节点Nnew是否为规划航线目标点Ngoal。若是，则转入 Step6；若否，则转入 Step2；

Step6：航线目标点Ngoal称为搜索树Υ中的一个叶节点，由Ngoal回溯到航线规划起始点Nroot。由可行路径中的节点序列生成航线关键点序列，规划输出；

输出：航线关键点序列。

算法中提到的新节点生成过程如图1所示。首先产生随机点Nrand并在搜索树中遍历到与其最近节点Nnear。在两节点组成的向量方向上，按固定步长截取计算新节点Nnew，其计算如式（1）所示。步长通常由无人机的性能确定，不小于无人机最短直线航段长度。式中，λ为扩展步长。

图1 搜索树新节点生成示意图

2 MO-RRT多优化策略设计

为说明优化策略的设计思路，将MO-RRT算法中搜索树的节点定义为一个四元组：

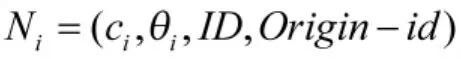
其中ci为无人机的三维位置坐标；θi为飞行方向；ID为该节点区别于其他节点的标识符；Origin-id表示该节点在搜索树中的父节点的ID，用于标识该节点在搜索树中的位置。

针对标准RRT算法的不足，对其提出适应性的优化策略。主要作出以下优化：①基于雷达跟踪机制的威胁规避；②基于目标启发的搜索树节点扩展；③基于冗余航线点裁剪的航线简化。

2.1 基于雷达跟踪机制的威胁规避

传统方法单纯地将雷达发现目标概率等同于单次扫描探测到目标信号的概率［12-14］。这种简化方法忽视了雷达作出目标发现决策所采用的“多次探测、形成跟踪”判定准则，使无人机难以充分发挥性能优势。

文献［16］对雷达威胁模型进行了概率形式的描述，从航线规划的角度，提出考虑目标跟踪机制的雷达威胁模型。本文将采用该模型进行防空雷达的威胁建模。

模型首先依据自身性能参数，通过雷达与目标无人机间的距离和无人机RCS幅值，解算出雷达对无人机的单次探测概率。进一步考虑防空雷达的目标跟踪机制，解算出雷达多次扫描对无人机形成的跟踪概率，将其与设定的判决概率阈值对比，确定无人机是否被发现。

2.1.1 雷达单次探测概率模型

为降低雷达对无人机的单次探测概率Psingle-d，航线规划可调节两者间的距离R。因此，根据雷达基本原理，可得［19］：

其中，c将其他系数进行整合，称为雷达综合比例系数，σ为雷达RCS幅值。

因此，在雷达的综合比例系数c已知的情况下，根据无人机相对雷达的RCS和二者距离便可求得雷达单次目标探测概率。由此，在航线规划中，可通过控制二者距离，降低雷达对无人机的单次探测概率。

2.1.2 基于跟踪机制的雷达跟踪概率模型

在单次扫描得到探测概率Psingle-d的基础上，雷达判定目标发现的决策还基于一定的跟踪机制，主要为以下两项：①在M个扫描周期中，不存在多于N次未探测到目标信号；②取得的目标信息满足跟踪需求或航线预测。若规划航线不同时满足两准则，则可实现其飞行安全，间歇式暴露航线便是一则良好的应用实例。

依据雷达探测跟踪目标成功概率Pm-track与Psingle-d的关系，实现基于目标跟踪机制的雷达发现目标模型。利用雷达与目标间的距离R及无人机目标的RCS幅值σ，可以表示雷达跟踪目标成功概率为：

式中，c1和c2是由防空雷达自身性能和设置参数决定的。

2.1.3 多雷达威胁模型

考虑到不同雷达的雷达波在发送与接收时均设定于不同的频域和时域区间［17］。本文提出的多雷达威胁模型中认为各部雷达之间探测跟踪是相互独立的。因此，考虑到在防空系统中，雷达之间是可以通信的，所以对无人机目标的跟踪概率可以表述为：

基于雷达目标跟踪机制的威胁规避策略利用时间窗滚动策略。雷达目标跟踪机制确认目标是在一定的时间段内对无人机进行周期性扫描得出的。因此，利用固定长度的时间窗将探测航点附近的航线选中。对探测航点的雷达发现概率计算实际上是对该段时间范围内航线的雷达发现概率的均值计算。当求得的无人机跟踪概率大于阈值Pac时，表明无人机在该点处被雷达跟踪。

利用以上判定准则，对待扩展航线点是否在敌方防空系统威胁空间进行检验。若在威胁空间中，则舍弃该待扩展航线点；否则，该点经其他约束条件检验合格后，可将其添加到航线点搜索树中。

2.2 基于目标启发的快速收敛

在标准RRT算法中，搜索树节点扩展方式的随意性明显导致其数量规模大、结构混杂，生成的航线仅具有可行性，而不具备优化性，所以标准算法的收敛性差。因此，提出基于目标启发的快速收敛优化策略，控制搜索树节点扩展，使算法能够迅速收敛于最优解。该优化策略主要体现在：①随机点Nrand产生；②待定节点Nundeter选择。

在产生随机点Nrand时，使一定概率产生的随机点Nrand取值为目标点，使目标点启发引导搜索树生长方向朝向目标点，加快算法收敛。在每次产生的m个待定节点Nundeter中，利用目标代价函数对其评估，选择最优点作为新节点Nnew添加到搜索树中，减少搜索树中性能较差的航线点。基于目标启发的快速收敛优化策略的具体算法流程如下。

输入：目标点选择概率阈值pgc（0＜pgc＜1）、单次循环随机点产生个数；

Step 1：产生区间（0，1）之间的随机数，并赋值于目标点选择概率Pg；

Step 2：比较 Pg与 Pgc，若 Pg＞Pgc，则转到 Step 3；否则，转到Step 4；

Step 3：将目标点赋值于产生的随机点，即Nrand=Ngoal；

Step 3.1：遍历搜索树，确定相应最近节点Nnear，根据移动步长，产生待定节点Nundeter；

Step3.2：判断Nundeter是否在威胁区Zthreaten，若Nundeter∉Zthreaten，则添加Nundeter到搜索树中，返回Step1；否则，直接返回Step 1；

Step 4：在规划区域内，产生m个随机点Nirand（i=1，2，…，m），确定各点的最近点 Ninear；

Step 4.1：对应产生m个待定节点Niundeter（i=1，2，…，m），根据目标函数Eq（5）对各个待定节点估算，取得最小值点Nmin；

Step 4.2：判断Nmin是否在威胁区内，若Nmin∈Zthreaten，则返回Step 1；否则，添加Nmin到搜索树中，返回Step 1。

优化策略流程中提到判断节点是否在威胁区内采用基于雷达跟踪机制的威胁规避优化策略进行解算决策。

航线规划问题模型的目标函数主要包含威胁代价函数、航线长度代价函数和航线转弯代价函数。因此，航线规划问题模型的目标函数如下式：

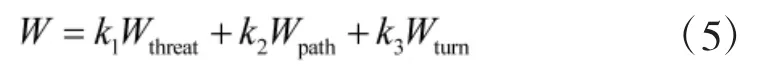
其中，Wthreat、Wpath和Wturn依次代表规划航线的威胁代价值、航线长度代价和转弯代价。目标函数中的三项分量在MO-RRT算法产生的航线性能方面的作用和影响，具体如下页表1所示。k1、k2和k3分别表示3种代价函数的权值系数，其满足关系式：0≤k1，k2，k3≤1 和 k1+k2+k3=1。三项权值系数可以根据具体规划需求动态设定。

表1 目标函数各项说明

待定航线点Niundeter（i=1，2，…，m）的目标函数中的三项权值分量的计算公式分别如下所示：

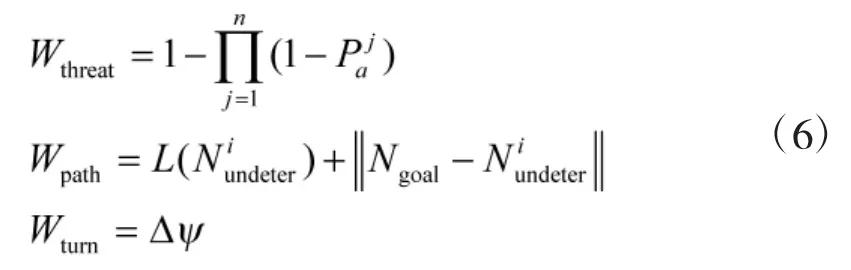
其中，n为区域中的敌方雷达数目，Paj为第j部雷达对Niundeter的跟踪发现概率。L（Niundeter）为航线从起始点到Niundeter所经历的路径长度，‖Ngoal-Niundeter‖为Niundeter到目标点的直线距离。△ψ为航向角的改变值。

2.3 基于冗余航点裁剪的航线简化

在搜索树中，各子节点仅对应一个父节点。起始点为唯一的根节点，采用倒溯法可以找出整条航线中的关键点序列。

由于算法中节点选取的随机性，使得航线节点序列中存在大量冗余节点。因此，为降低飞行距离，并减少对无人机飞行状态的调整，对航线中的冗余节点进行裁剪。

冗余节点裁剪主要考虑两不相邻航点间连线是否穿过威胁区。若不存在威胁，则两节点间的节点均视为冗余。其流程如下：

输入：初始航线节点序列为{p1，p2，…，pn}，其中p1和pn分别为航线的起始点和目标点；

Step1：构建冗余节点裁剪后的精简航点序列集合Γ，该集合初始为空集；

Step2：将目标节点pn添加到集合Γ中，令j=n、i=1；

Step3：检查航线节点pj与pi间是否存在威胁，若存在威胁，转入Step4；若不存在威胁，转入Step5；

Step4：若 i=j-1，则设 j=j-1、i=1，转入 Step3；否则 i=i+1，转入 Step3；

Step5：将节点pi加入精简航线节点序列集合Γ，并令j=i、i=1。若 j=1，则冗余节点裁剪结束；否则，转入Step3。

输出：精简航线关键点序列。

3 实时航线规划算法

实时航线规划要求无人机在有限的探测能力下，在遇到威胁致使航线失效时，能够快速生成新的规划航线。

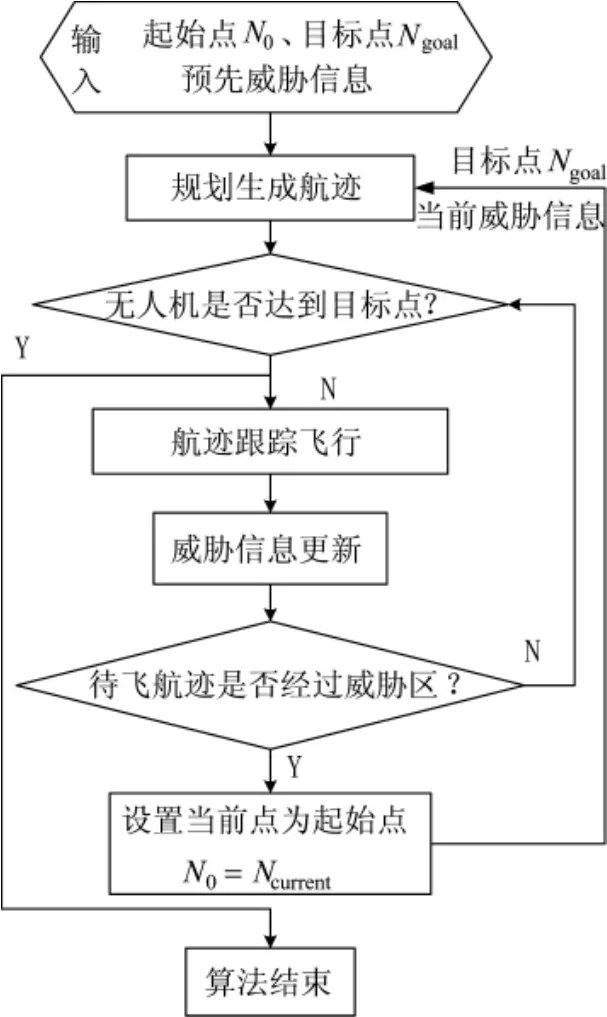
图2 基于MO-RRT的无人机实时航线规划

无人机在依据预先规划航线飞行时，其不断对周围的环境进行探测。若没有未知威胁出现，则无人机跟踪预先规划航线飞行，直到抵达目标点。若出现突发威胁时，判断待飞航线是否经过威胁区域，若经过，则将当前飞行位置点设为起始点，对航线进行重新规划，无人机按新产生的航线飞行。如此循环，直到无人机到达目标点。

4 仿真实验

4.1 仿真环境

为验证基于MO-RRT的无人机预先/实时航线规划算法的有效性，对其进行仿真实验。仿真试验中算法涉及到的参数设置具体见表2所示。

表2 算法仿真实验参数设置

RRT算法的随机性使得相同条件下的各次规划结果存在差异。为消除随机性影响，对各算法执行1 000次实验，统计各项规划结果的平均值。

4.2 实验结果与分析

4.2.1 优化策略验证

设置规划范围为60 km×60 km的区域，目标点的坐标为（10，10），终止点为（59，59）；雷达的部署位置为（30，30）。图3中两幅图依次表示在标准RRT算法和MO-RRT算法规划下的航线生成图。

图3 不同优化策略下的规划生成航线

对不同优化策略下的两种算法的千次仿真实验的性能结果数据统计如表3所示。

表3 两算法规划航线性能比较

由以上对比可知，标准RRT算法生成的搜索树节点数量大（2 034.2）、形状复杂，生成航线不具备最优性。而MO-RRT算法的平均搜索树节点数为118.4，能有效降低搜索树规模，加快算法收敛。同时，通过比较飞行距离均值可知，标准RRT算法生成的航线严格处于雷达威胁区域外（图中灰色区域），增加了航线长度；而MO-RRT算法生成的航线则以较短航线穿越雷达最大探测范围，又确保不被雷达发现。

4.2.2 实时航线规划验证

MO-RRT算法的实时航线规划仿真验证实验通过在复杂战场环境下进行。图4为MO-RRT航线实时规划执行过程中的各个典型阶段。

图4（a）表示根据战场中已知的威胁进行的预先航线规划（绿色粗线为预先规划航线）；无人机按航线飞行时，在某一航点探测到前方存在突发威胁，如图4（b）所示，蓝色线条表示已飞航线；进而触发MO-RRT航线实时规划算法以当前点为实时规划起点，进行航线实时重规划，如图4（c）所示，红色线条为实时重规划航线；图4（d）为依据重规划航线飞行的无人机航线。

航线的实时重规划性能主要从重规划时间、航线节点数及航线长度体现。MO-RRT算法对上述场景进行千次实验，得出其重规划时间为180 ms，能够为规避突发威胁提供充足时间。此外，重规划航线节点个数为83、航线长度为247.02 km，保证了实时规划航线的稳定性和优化性。

图4 实时航线规划过程

5 结论

本文提出的基于MO-RRT无人机实时航线规划算法，实现无人机在高密度雷达威胁的战场环境下规避突发威胁并实现最优飞行航迹。该算法充分利用RRT算法随机采样的优点，同时考虑雷达的跟踪准则提高航线安全性，目标启发策略进一步加快算法的收敛速度，使算法具备实时性。通过裁剪冗余节点，有效降低了航线长度，并减少了大量不必要的无人机姿态调整。仿真结果表明该算法具备良好的实时性和优化性，算法具备一定的理论和应用价值。

［1］魏瑞轩，李学仁.无人机系统及作战使用［M］.北京：国防工业出版社，2009.

［2］姚敏，王绪芝，赵敏.无人机群协同作战任务分配方法研究［J］.电子科技大学学报，2013，42（5）：723-727.

［3］郜晨，甄子洋，龚华军.雷达威胁环境下的多无人机协同航迹规划［J］.应用科学学报，2014，32（3）：287-292.

［4］JEAN B.A new mixed-integer linear programming model forrescue path planning in uncertain adversarial nvironment［J］.ComputerandOperationsResearch，2012，39（12）：3420-3430.

［5］WILLIAMS P.Three-dimensional aircraft terrain-following via real-time optimal control［J］.Journal of Guidance，Control and Dynamic，2007，30（4）：1201-1205.

［6］PENG C，LU X Q，DAI J Y，et al.Research of path planning method based on the improved Voronoi diagram［C］//Proc.of the 25th Chinese Control and Decision Conference，2013.

［7］魏瑞轩，许卓凡，王树磊，等.基于Laguerre图的自优化A-Star无人机航路规划算法［J］.系统工程与电子技术，2015，37（3）：577-582.

［8］JU M Y，CHENG C W.Smooth path planning using genetic algorithms［C］//Proc.of the 9th World Congress on Intelligent Control and Automation，2011.

［9］ZHAO S G，LI M.Path planning of inspection robot based on ant colony optimization algorithm［C］//Proc.of the International Conference on Electrical and Control Engineering，2010.

［10］FOO J L.Path planning of unmanned aerial vehicle using B-splines and particle swarm optimization ［J］.Journal of Aerospace Computing，Information and Communication，2009，6（4）：271-290.

［11］LAVALLE S M，KUFFNER J J.Randomized kinodynamic planning［J］.Int J Robots Res，2001（20）：378-440.

［12］郑文昌，李磊，徐帆江，等.基于进化算法的无人飞行器多航迹规划［J］.宇航学报，2005，26（2）：223-227.

［13］黄长强.无人作战飞机精确打击技术［M］.北京：国防工业出版社，2011.

［14］阮颖铮.雷达截面与隐身技术［M］.北京：国防工业出版社，1998.

［15］高龙波，李本威，张赟.无人机远航工作轨迹优化研究［J］.兵器装备工程学报，2016，36（3）：94-97.

［16］FRANK W M.Radar cross-section reduction via route planning and intelligent control［J］.IEEE Transactions and Control Systems Technology，2002，10（5）：696-700.