多帧超分辨率图像重建迭代小波算法研究

2018-01-15付亚伟魏镜弢赵明

价值工程 2018年1期

付亚伟+魏镜弢+赵明

摘要：为了解决由于物体的运动和拍摄环境等因素，造成拍摄后多帧图像分辨率低和细节丢失的问题。本文对现有超分辨图像处理算法查阅研究，提出超分辨率图像重建迭代小波算法。最终对比迭代小波算法运算后最终的图像和参考帧图像，并比较图像信噪比的变化得出迭代小波算法的优越性。

Abstract： In order to solve the problem of low resolution and missing details of multi-frame images after shooting because of the object's movement and shooting environment， in this paper， the current super-resolution image processing algorithm is researched， and the super-resolution image reconstruction iterative wavelet algorithm is proposed. In the end， the final image and the reference frame image after the iterative wavelet algorithm operation are compared and the superiority of the iterative wavelet algorithm is obtained by comparing the changes of the signal to noise ratio of the image.

关键词：细节丢失；超分辨率图像；迭代小波算法；信噪比

Key words： loss of detail；super-resolution image；iterative wavelet algorithm；Peak Signal to Noise Ratio

中图分类号：TP391.4 文献标识码：A 文章编号：1006-4311（2018）01-0214-02

0 引言

超分辨率图像重建是指使用一定的图像处理方法，将一系列低质量、低分辨率图像转化为产生高质量、高分辨率的图像[1]。目前，这种方法应在生活中，由于客观条件的限制，如交通过程中使用的摄像头、卫星拍摄时用的摄像头等设备。使拍出来的照片会存在不同程度的损伤和视野模糊不清且分辨率很低，造成图像细节的丢失的还原的情况。

1 现有主要图像细节还原算法简介

超分辨率图像重建的算法有很多种，其中一种为空域算法[2]，这种算法是在假定二维平移的条件下，利用插值和去模糊技术消除了相机镜头的模糊。此方法假定模糊函数不但在整副图像上是一致的，同时也都受到全局二维平移的限制。

后来有人又提出图像重构加权算法。图像重构加权算法即是把已经放大的每帧低分辨率的灰度图片以不同的权重叠加为一个新的图片的方法。通常采用下面的数学模型：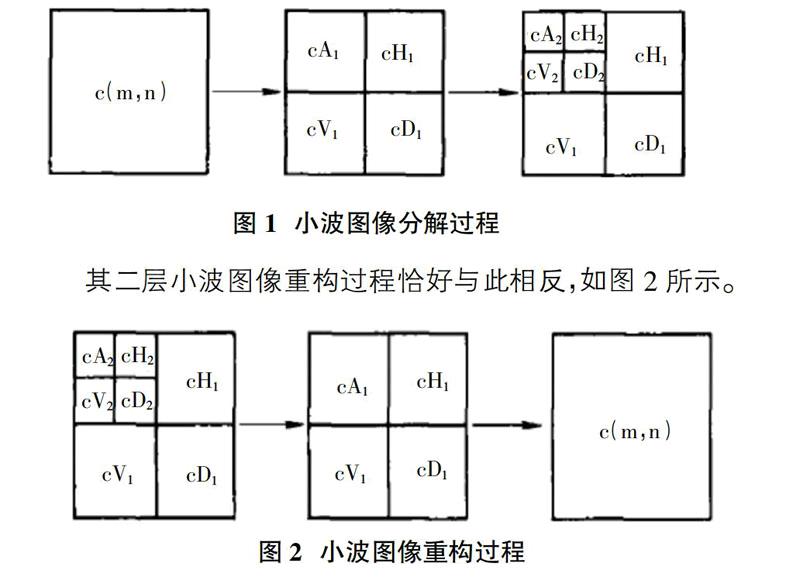

B=x0·A0+x1·A1+…+xi·Ai（1）

其中Ai（i=0，1，2…）为低分辨率的图像序列，B为重建图像，xi为每一帧图像的权重，且需要满足下面的数学关系式：∑Xi=1。但是这种算法存在明显的缺点：受权重系数的影响较大，理论上细节较多的图像权重应该更高，细节较少的图像权重越小。由于在加权过程中，自然会把图像的噪声带入其中，所以一般情况下，图像帧数不易过多且细节较少的图像应该过滤掉。

林宏裔等人做了在MATLAB环境下基于小波变换的图像处理[3]，这种方式是将二维图像在不同的尺度上进行二维离散小波变换分解，分解的结果为：近似分量cA、水平细节分量cH、垂直细节分量cV和对角细节分量cD。反过来，又可以利用二维小波分解的结果在不同尺度上重构图像，二维离散小波分解原理是：

其二层小波图像重构过程恰好与此相反，如图2所示。

从其分解重构过程可以知道小波分解实际上是信号不断”剥落“的过程，而粗尺度近似部分即为丢掉高频细节信息的低分辨率图像。因此想得到高分辨率图像，只需要在低分辨率图像上加入需要的细节信息，再进行小波重建就可以了。

后来，在前人研究的算法的基础上，有科学家提出了迭代背投影算法，这种算法使以一个初始的猜测值开始，反复的模拟成像过程，再将误差返回给超分辨率图像以不断修正，最后得到较理想的结果。这种算法能处理一般的運动及不同的模糊函数[4]。

北京交通大学宋琼等人提出了超分辨率图像处理的一种IBP算法[5]。这种算法产生高分辨率的过程是一个重复的迭代过程。首先假定初始值f（0）是要得到的结果，模拟成像过程可以得到一个低分辨率图像的集合{gk（0）}。如果f（0）是正确的高分辨率图像，则得到的这一集合就应该和已知的低分辨率图像序列集合相等。而通过将它们之间的差值{gk-gk（0）}返回给f（0）中相应的区域可以改善f（0）得到一个相对较接近正确结果的f（1）反复迭代该过程使下述误差函数达到最小值。

2 迭代小波算法简介

本文针对以上算法的优点和缺点，提出迭代小波算法，这种算法的理论是首先选取参考帧，然后分别把参考帧和第二帧、第三帧和第四帧图像运用sift算法进行图像配准、然后进行小波算法分解重构。对小波算法重构后的图像再一次进行sift算法图像配准，使用小波算法进行分解重构。最终迭代多次得到重构图像。由于迭代次数与选取低分辨率图像的帧数有关，但是随着帧数的增加数据计算量增大[6]。所以本文选择四帧图像作为实验，证明小波迭代算法有效。其算法结构流程图如图3。endprint

3 实验步骤及实验结果

①通过MATLAB中RGB图像转换为灰度图像的函数方法，分别把四副图片转换为灰度图片；再利用MATLAB中内置的imresize（）函数分别把四副图片（注：四幅图片是在不同环境下拍摄）转换为32×64的低分辨率图像，得到结果如图4所示。

②接下来是四副图片的运动估计，首先选择第一帧低分辨率的图片为参考帧，即为A0，其余帧低分辨率图像分别记为A1，A2，A3；运用sift算法分别找到四帧图片相对于参考帧的特征点，然后用参考帧分别与其余帧图片进行特征点的匹配。

③在第二步中通过特征匹配已经得到第二帧关于第一帧的相对位置，即运动的距离和方向。接着对着两副低分辨率的图像进行图像序列重叠然后用双线性三次插值法对第一帧低分辨率图片即参考帧进行放大处理。

④根据上文提出的迭代小波重构算法，对四副图片重新进行融合重构，最终得到重构图像如图5。

⑤相较于参考帧，可以看出部分细节得到还原。虽然从视觉上观察得出有某些细节被还原出来，但是效果不是很明显，肉眼观测也不是那么直观。

⑥选择迭图像的信噪比这一参数进行定量分析：选择第一帧低分辨图像作为参考帧，迭代小波算法重建后的小波图像信噪比（PSNR）[7]变化如表1。

4 结论

①通过迭代小波算法重构图像与参考帧进行对比分析，证明通过使用迭代小波重构算法使图像的部分细节得到还原。

②通过计算每次使用迭代小波重构算法后图像信噪比在表中横向上的变化，可以看出逐渐增大，说明图像细节得到还原，证明迭代小波算法有效。

③多帧低分辨率序列图像的细节还原模型为视频的细节还原研究提供重要参考意义。

参考文献：