生命和素数都有基因吗？

王 鑫

人类现在已经进入21世纪了,这是一个数字化的时代。几乎所有的信息都可以数字化。数字无所不在。数字里素数是最为神秘的，但是人们对于素数尤其是素数之间的关系知道的并不太多。大家在媒体上常常听说的孪生素数、哥德巴赫猜想和陈景润的故事都是和素数有关系的。这些研究工作的主要目的是寻找素数的规律或者素数之间的关系。

生命目前为止是只在地球上出现的物质运动形式。我们人类只是其中一种。聪明的人类几乎什么都知道，但是面对素数我们确实有点犯难：确实素数看起来有点杂乱无章。那么素数和同样复杂而又变化多样的生命之间有没有什么相似之处呢？

素数和生命两个看似毫不相干的东西确实有相同之处，就是二者都是不那么驯顺而充满例外、因而吸引了无数好奇心十足的爱好者的神经。生命在地球上有了几十亿年的历史了，其间生命变化多端花样不断翻新，异彩纷呈，层出不穷，让人看得眼花缭乱。那么生命最后会有终点么？物种的数目有上限吗？同样的问题，也可以问素数。目前人们已经找到的最大的素数有一千多万位。把这个数字打印出来就是一本很厚的书啊！其实这么大的素数还远没有到头儿，还有更大的素数等着人们去发现呢。好奇的人也许要问，素数有没终结的时候？好像是没有！

乍看起来，素数和生命的不同之处在于生命是有传宗接代的现象的，有遗传，有内在基因联系。那么，素数之间有这种关系吗？如果有，又是怎么个关系呢？看看下面的图，也许你会发现素数实际上是有基因遗传的。

首先看看211以内的素数，看看你能看出什么规律来

2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97，101，103，107，109，113，127，131，137，139，149，151，157，163，167，173，179，181，191，193，197，199，211

一头雾水吧？估计你没看出来什么规律来吧。分成几段，也许不一样，试试看。左边是素数，右边是总结的规律。

到这儿，你也许看出点门道了，让你自己去继续，聪明的你也许自己会写下：

到此，你已经修练得差不多了。素数不管多大，按照这个规律你都能轻松地逮住它，因为你掌握了素数增殖的规律了。但是，别高兴太早，看见那些黑框里的数了吗？它们是例外的，它们不是素数，还得想办法剔除。

现在你也许发现，你们家的纸不够用了。没钱买纸也许是很多人不能成为数学家的一个重要限制因素啊！

把这些数字用图画出来也许能够看出更大范围内的规律来。前几十个素数看起来是这样的:

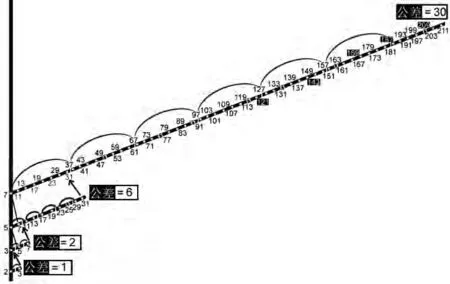
如果把观察范围放大到几十亿、上百亿，素数的谱系树看起来是右图所显示的样子。

大范围和小范围的规律看来是差不多的！看起来素数还是挺好玩的，有一定的规律可循，没事儿就不妨多玩玩儿吧。

现在再回头仔细看看，上面的信息告诉了我们什么？

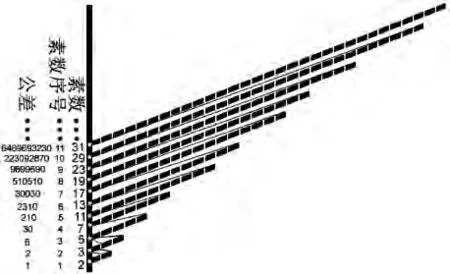
1.所有的素数构成一个巨大的、无限生长的树。每一分枝上的素数来自一个方阵，第n代的素数方阵的行数为第n个素数的值，第一行由第n-1代的所有素数（除去第一个素数）组成，从第二行起每一行中数字的值是上一行的数值加上公差构成，第n代素数由第n个素数引领。素数方阵的每一列构成一个等差数列，公差值等于第n-1个素数的素数积（小于第n个素数的所有素数的乘积）。

2.素数之间虽然不是普遍联系的，但是几乎每一个素数都有其祖先、后裔、兄弟姐妹，好像物种在演化网络中的角色一样。后续的素数是前面素数的组合。组合不同，素数的数值不同，就像每个物种的特征都是其祖先既有特征的不同组合，新的组合构成新的物种，不同的组合构成不同的物种。

3.按照上述规律推算出来的数不全都是素数，有例外（黑框里的数），就像物种有败类和灭绝现象一样。

4.例外是规律甩不掉的影子，就像物种和其演化规律一样，物种的灭绝是由于遇到了其祖先也无法应对的挑战。按照上述规律算出来的数之所以不是素数不是因为按照上述规则构成它的素数有问题，而是因为后续出现的新的素数能整除它，就像物种的灭绝不是其祖先有问题，而是它和后来的境遇之间的关系决定的一样。

5.孪生素数（下划线者）的祖先也是孪生素数，就是说，所谓的孪生素数很可能具有一定的遗传性。

6.没有永远不变的规律。规律只在一定范围内起作用。进入新的阶段，规律的组合也会发生变化，即有更新的规律出现并发挥作用。

7.老的规律可以隐藏在新的规律内，新的规律可以包含老的规律。

素数与生命给与我们的启示

素数与生命都是无限的，不会有尽头。按照上述规律推算出的数字也许不是素数，如同某些物种也许会灭绝一样，但是素数和生命整体都不会有完结的终点。

素数与生命都有前世和后世，也都有其起源、延续、繁衍和灭绝的过程，了解这个过程及其背后的规律对我们利用它们为人类幸福服务有着类似的重要意义。