基于边界值方法的微分动力系统快速数值计算方法

陶静静 潘明帅 汪芳宗

(三峡大学 电气与新能源学院,湖北 宜昌 443002)

微分动力系统是研究随时间变化的动力系统的整体性质及其在扰动中的变化.对微分动力系统的研究通常可以归为一阶微分方程问题的求解,微分动力系统中高维非线性问题归根结底是微分初值问题(initial value problem,IVP).有关微分初值问题的研究,已经获得了丰富的研究成果.其中,具有重要影响且具代表意义的数值方法大致包括:Runge-Kutta方法(RK methods)[1],微分求积法(differential quadrature methods,DQM)[2-4],线性多步法(linear multistep formulae,LMF)[1],边界值方法(boundary valuemethods,BVM)[5-6]等.

在实际工程应用中,隐式梯形法因具有单步A-稳定性和二阶精确度而被广泛使用.虽然隐式梯形算法对于逐步积分计算很容易,但仍然存在计算效率问题.由于该算法是单步和低阶数值积分方法,因此在实际应用中不能选择过大的积分步长,从而将不仅会增加积分步数,而且会损失由太多积分步数带来的累积误差,降低计算精度.为了克服单步数值法的不足,人们开始考虑多级高阶整合算法,其中RK方法被广泛研究.虽然RK方法具有良好的数值稳定性,但是却很少应用到实践当中.这是因为当微分动力系统的维数增大时,容易引起阶障碍,也就是所谓的Dahlquist障碍(Dahlquist barriers)[7],这个问题同样也出现在微分积分方法的求解中.对一个m维的非线性微分初值问题,s级的隐式RK方法在每一步的积分过程中需要求解s×m维非线性方程联立的方程组;当m很大时,其巨大的计算量让人难以接受.Brugnano等学者为了克服LMF类方法所存在的稳定性及阶障碍,提出一系列新的方法,称之为边界值方法[5].Brugnano将BVM分为3类[6],分别为:扩展的梯形积分方法(extended trapezoidal rules,ETRs);广义BDF方法(generalized backward differentiation formulae,GBDF);广义Adams方法(generalized Adams methods,GAMs).概括起来,BVM类方法在保持LMF类方法所具有的多级高阶优点的同时,避免了高阶LMF方法所存在的稳定性问题,因而具有潜在的应用价值.然而,BVM的现有研究主要针对线性微分动力学系统提出,限制了这类方法的应用.

基于上述思路,本文将ETR2方法应用于非线性微分动力系统数值计算,提出了一种新的数值计算方法.所提方法的主要优点:基于边界值方法的高阶特性,该方法可以采用更大的积分步长,由此可以减少数值积分的步数;基于整体雅可比矩阵所具有的特殊带状结构特征,采用适当的矩阵方程分裂技巧,避免了对高维的整体雅可比矩阵或多个分块子矩阵进行三角分解,因而提高了计算效率.

1 ETR2方法简介

以下述一阶常微分初值问题为例:

基于均匀网格的s级的ETR2方法可用下述公式来描述:

式(2)中βi,i∈(0,μ-1)的取值可参见文献[6];

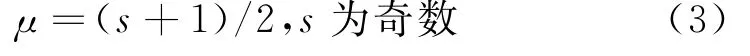
s级的ETR2方法(2)是A-稳定、s+1阶的数值方法,其稳定域与传统的隐式梯形积分方法的稳定域完全一致[6,8].作为示例,当s=3时,上述方法(2)的具体表达式为:

与传统的“逐步积分”求解过程不同,将BVM方法应用于初值问题时,只能利用积分规则在多个时间点上连续进行离散,然后对离散后的方程进行整体求解.另外,顾名思义,将边界值方法应用微分方程的数值计算时还需结合相应的边界条件.若将该方法应用于方程(1)的数值求解,则需要已知x0,x1,…,xv-1以及xN-s+v+1,…,xN等s个边界值.然而,对微分初值问题而言,通常只有x0是已知的.因此,将边界值方法应用于初值问题时,必须将边界值方法与所谓的附加方法(additional methods)[5-6]联合起来,以便形成与待求点数N相匹配的N个方程.为此,Brugnano等学者提出了附加方法的选择策略[5],具体可概括如下:附加方法与采用的边界值方法应相互独立,但两者应具有相同的阶数.依据上述策略选择的附加方法,将不会影响边界值方法作为主体方法的数值稳定性及计算精度.

2 基于ETR2方法的微分初值问题数值计算方法

以3级4阶的ETR2方法(4)为例.

采用该方法时,需要利用附加方法形成2个附加方程.由于ETR2方法(4)是对称的方法(symmetric method),因此,不能选择该方法的反射方法作为附加方法,但可以选择同阶的、非对称ETR2方法[9]作为附加方法.

以方法(4)为主体方法,选取以下方法作为时域始端的附加方法:

同时选取以下方法作为时域末端的附加方法:

利用方法(4)、(5)及(6)对方程(1)进行连续的时域差分离散,然后利用牛顿法对离散后的方程进行整体求解,可得

式(7)中:

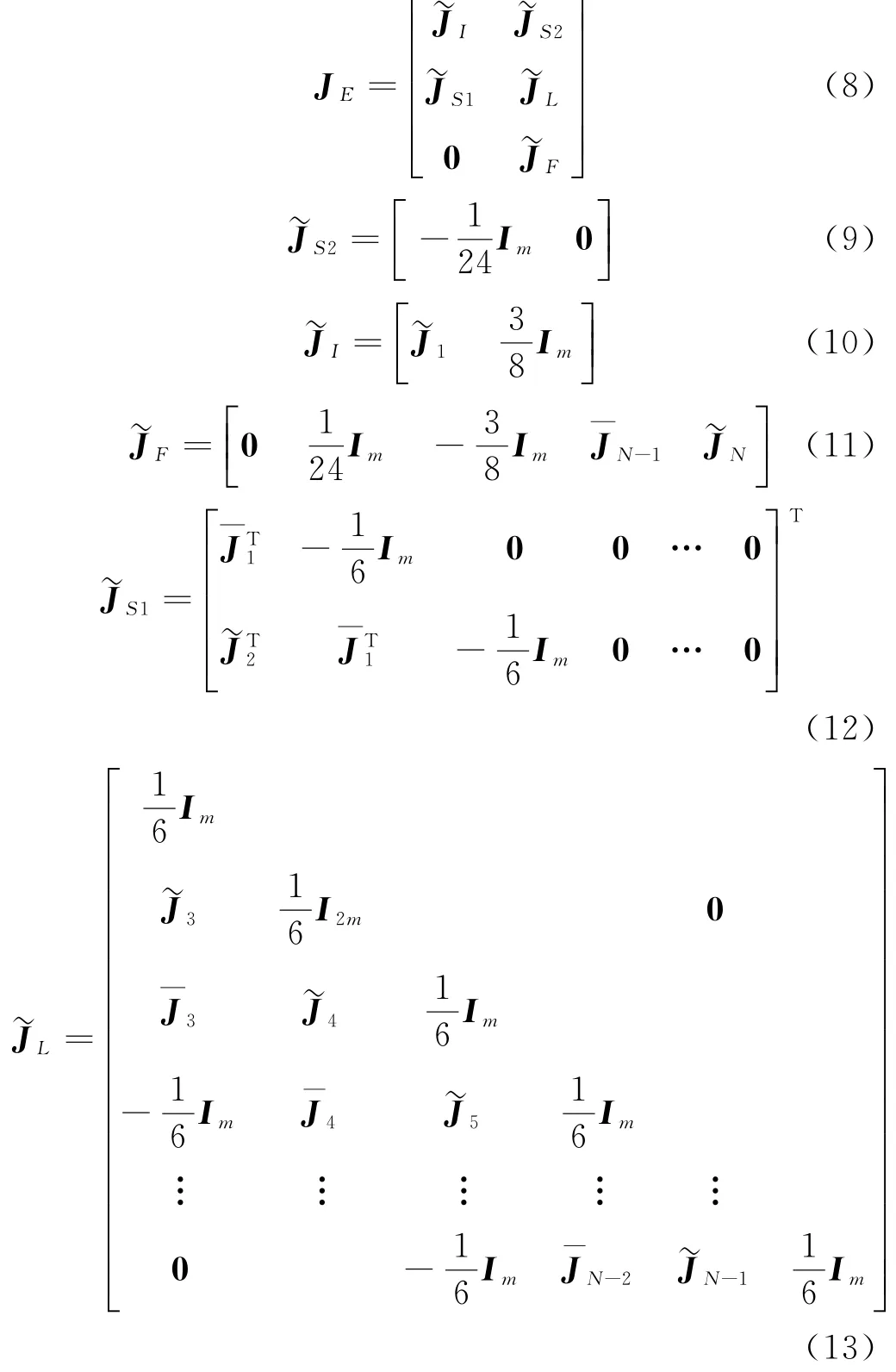
上述表达式中:

下面介绍牛顿方程(7)的快速求解方法.依据JE的结构特征,可以将方程(7)分解为以下3个方程组:

上述3个方程中:

在导出关系式(25)后,将其代入方程(20)和(21),最终可以导出一个关于的矩阵方程组.为方便起见,将这个矩阵方程组用式(26)表示:

显然,在涉及N个网格点的积分求解过程中,上述求解方法只需对一个2m维的方阵进行三角分解.概括起来,对s级(s为奇数)的ETR2方法,上述求解方法也只需对一个(s-1)×m维的方阵进行三角分解.

3 数值算例及分析

大规模电力系统是典型的高维非线性微分动力系统,以采用经典模型的电力系统暂态稳定性数值计算为例.在此情况下,电力系统暂态稳定性计算的数学模型可用以下微分方程组来描述[8]:

上式(27)中:i∈(1,p),p为发电机的数量;δi,ωi分别为发电机的功角与角频率;Mi为发电机的惯性时间常数;Pmi为发电机的机械功率;Cij、Dij均为常量.

隐式梯形法是属于线性多步法的一种,因为其出色的数值稳定性在电力系统领域被广泛应用.显然,其每一步的求解可用式(28)来描述:

式(28)中:上标ki表示该步积分的迭代次数.

很易理解:若用隐式梯形法积分N步,则该方法总共需要对N×ki个m维的矩阵Hi,i∈(1,N)进行三角分解,这里的ki即是隐式梯形法在第i步的积分中所需的迭代次数;若在每一步的积分求解中采用定雅可比牛顿法或隐式梯形法(very dishonest Newton method,VDHN),则该方法总共需要对N个m维的矩阵Hi∈(1,N)进行三角分解.若采用本文所述的方法积分N步,则总共需要对η个(s-1)×m维的矩阵进行三角分解,这里的η即是该方法所需的迭代次数.因此,从理论上讲,若η＜＜N,则本文所提出的计算方法在计算效率上将比隐式梯形法具有优势.

首先选用IEEE145节点系统[10]作为算例系统(简称算例1).该系统含50台发电机(p=50,m=100).暂态稳定性计算中,故障设定为在7号母线处发生三相短路,经0.1 s后切除.利用该算例系统,将本文所提出的方法与隐式梯形法进行对比测试.对比测试中,对2种方法设定相同的收敛精度,即‖∇R(X)‖≤ε=10-5,‖∇r~(xi)‖≤ε=10-5.为便于对计算精度进行对比分析,利用中国电科院的PSASP程序同时采用0.001 s的小步长进行暂稳计算,将所得的计算结果作为基准,以此来跟踪、观察不同算法的计算误差曲线.

图1是利用隐式梯形法(h=0.02 s)和3级4阶ETR2方法(N=40,h=0.04 s)所计算出的几台发电机功角摇摆曲线,其中采用严格牛顿法的隐式梯形法每一步的积分需迭代2～3次,即ki=2～3,3级4阶ETR2方法需迭代5次,即η=5,图2是2种方法所得结果相对于基准结果的误差曲线(故障切除后).

从图2可以看出:3级4阶ETR2方法在采用较大的步长的情况下,其计算精度仍优于采用较小步长的隐式梯形法.

另选一个大规模电力系统作为算例系统(简称算例2).该系统含327台发电机(p=327,m=654)、2 383个节点[11].暂态稳定性计算中,故障设定为在171号母线处发生三相短路,经0.1 s后切除.设定如上所述的、相同的收敛精度,将本文所提出的方法与隐式梯形法进行对比测试.

图1 两种方法所得发电机功角摇摆曲线(算例1)

图2 两种方法所得结果的误差曲线(算例1)

图3 两种方法所得发电机功角摇摆曲线(算例2)

图3是分别利用隐式梯形法(h=0.02 s)、3级4阶ETR2方法(N=40,h=0.04 s)所计算出的几台发电机功角摇摆曲线,其中(采用严格牛顿法的)隐式梯形法每一步的积分需迭代2～3次,即ki=2～3,3级4阶ETR2方法需迭代6次,即η=6.

图4是2种方法所得结果相对于基准结果的误差曲线(故障切除后).从图4可以看出:3级4阶ETR2方法在采用较大的步长的情况下,其计算精度仍略优于采用较小步长的隐式梯形法.

图4 两种方法所得结果的误差曲线(算例2)

表1是对两种不同方法的计算速度的测试结果.

表1 两种不同方法的计算速度测试结果

从表1可以看出:本文所提出的计算方法在计算效率上明显优于隐式梯形法.

4 结 论

本文将ETR2方法应用于求解非线性微分动力系统,提出了一种新的快速数值计算方法.该方法作为边界值方法新的应用方式,具有高阶、数值稳定性好等优点.同时,本文所提方法是利用ETR2方法进行求解,在数值计算的过程中,充分利用ETR2方法本身的结构特点,采用适当的矩阵分解重构技巧,避免了迭代过程中对大型雅克比矩阵分解产生的大量计算,因此显著地提高了数值计算效率.

理论分析和仿真测试结果表明:本文所提出的基于ETR2方法的快速数值计算方法,在计算效率上比基于隐式梯形积分规则的数值计算方法具有明显的优势.

[1] Butcher J C.Numerical Methods for Ordinary Differential Equations,Second Edition[M].New York:John Wiley&Sons,2008.

[2] Bellman R,Casti J.Differential Quadrature and Longterm Integration[J].Journal of Mathematical Analysis and Applications,1971,34(2):235-238.

[3] 汪芳宗,廖小兵.基于微分求积法及V-变换的大规模动力系统快速数值计算方法[J].振动与冲击,2016,35(3):73-78,128.

[4] 汪芳宗,廖小兵,谢 雄.微分求积分的特性及其改进[J].计算力学学报,2015,32(6):765-771.

[5] Brugnano L,Trigiante D.Solving Differential Problems by Multistep Initial and Boundary Value Methods[M].Amsterdam:Gordon and Breach,1998.

[6] Brugnano L,Trigiante D.Boundary Value Methods:the Third Way between Linear Multistep and Runge-Kutta Methods[J].Computers&Mathematics with Applications,1998,36(10):269-284.

[7] Dahlquist G.Convergence and Stability in the Numerical Integration of Ordinary Differential Equations[J].Journal of Mathematica Scandinavica,1956,4(4):33-53.

[8] 倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002.

[9] Amodio P,Brugnano L.Parallel ODE Solvers Based on Block BVMs[J].Advances in Computational Mathematics,1997,7(1):5-26.

[10]Milano F.An Open Source Power System Analysis Toolbox[J].IEEE Trans.on Power Systems,2005,20(3):1199-1206.

[11]Zimmerman R D,Mueillo S X.MATPOWER:Steadystate Operations,Planning,and Analysis Tools for Power Systems Research and Education[J].IEEE Transactions on Power Systems,2011,26(1):12-19.