基于Benders 分解的煤炭供应链设备维护计划决策
2018-01-15郑澜波
刘 茜,郑澜波
(武汉理工大学 物流工程学院,湖北 武汉 430063)
1 引言
我国是世界上最大的煤炭生产与消费国,由于煤炭生产与消费地理的不平衡,煤炭行业形成了煤炭生产、输送、消费的供应链,煤炭供应链的可持续发展对国民经济具有重大影响,而煤炭行业的均衡、稳健发展依赖于设备的安全、可靠运转。随着设备向大型化、专业化及自动化方向发展,设备的维护管理问题日益突出。当前煤炭行业内的企业各自独立的由经验丰富的维修工人根据生产计划制定维护计划,这种分散的维护计划使得供应链上各企业的生产运作不均衡,造成了供应链整体效率较大的损失。
工业领域和学术界针对设备维护管理展开了研究。国内对煤炭行业设备维护的研究主要集中在:(1)设备管理制度和管理信息系统的探讨;(2)状态监测和故障诊断技术[1]。陈文静[2]、刘艺杰[3]介绍了维修管理理论,自修、外包等维修组织形式,指出现有设备维修体制存在的缺陷、维修决策水平不足、设备维护信息系统不完善等问题,并提出基于可靠性理论的设备预防性维护策略。范体军[4]提出设备维护外包的三种外包策略,并分析了不同策略对设备维护计划组织的影响。设备维护计划的决策研究已有部分成果。崔维伟[5]考虑生产与设备维护的集成调度问题,认为工件生产与设备维护相互关联、共同影响车间的生产效率,构建了以工件流程时间最短、维修成本最小的多目标模型,并设计出一种改进的遗传算法进行求解,实现了车间生产调度与设备维护计划的有效协调。然而上述研究没有考虑维修设备的关联性,对此,王红等人[6]提出故障链的概念对维修部件间的关系进行描述,建立了具有故障相关关系的复杂机械系统中各部件的可靠度模型。当前国内对煤炭行业的设备维护管理的研究还停留在维护管理模式及组织形式的探讨上,少数关于维护计划的决策研究对象或者局限于系统的一部分,或者没有考虑预防性维护的动态性,没有成果刻画制定的设备维护计划对持续生产的影响,更没有研究煤炭供应链上多个企业从宏观层面结成维护的战略联盟,协同制定预防性维护计划以降低维护中断对持续生产系统造成的影响的成果。本文从设备维护计划对降低煤炭供应链吞吐量影响的角度展开研究,揭示其中规律,为系统设备维护规划与管理提供科学决策。
猎人谷煤炭供应链协调机构数据显示,设备年度停机维护造成的系统中断会导致年吞吐量约15%的损失。猎人谷煤炭供应链协调机构协调供应链中各环节设备的维护窗口,分配容量,以使得计划期内因维护造成的吞吐量损失最少。Natashia Boland等人[7]利用“带边中断动态网络最大流(简称MaxTFFAO)”模型来研究煤炭供应链中设备维护的计划,清晰地阐明了带边中断动态网络最大流问题的结构特点。由于该问题的强NP难性,已有的多数方法均为启发式算法。Benders分解算法(以下简称BD算法)是一种运用分解思想求解混合变量规划问题的巧妙方法[9],将原问题分解为主问题(Master Problem,简称MP)和子问题(Sub-problem,简称SP),它适用于MaxTFFAO问题的求解,实验证明了BD算法的可行性和有效性。
2 问题概述
2.1 动态网络结构及最大流
图1表示一个煤炭供应链网络G=(V,A,C),左侧为铁路网络,右侧椭圆内为煤码头作业网络。左侧圆圈表示装煤点,方框表示煤炭汇集的铁路站点。码头中的大圆圈表示堆场。A为有向弧集,表示煤炭在设施设备间的流动轨迹:煤炭装载流、铁路输送流以及倾货、堆料、取料、装船和离泊作业流。煤炭需求量、铁路运煤能力、码头机械设备的工作能力分别表示相应弧的容量C。煤矿装煤中断、铁路因维护而中断、煤码头中机械设备停机维护都会使得煤炭供应网络的弧断开,弧容量降为零,造成该段时间内网络煤吞吐量减少;而维护结束后,弧容量恢复,即网络中弧的容量随维护的实施而变动。选择码头一段时期内输出煤炭量这一指标来评估供应链的效率,可见猎人谷煤炭供应链优化问题本质上是一个带边中断的动态网络最大流问题。
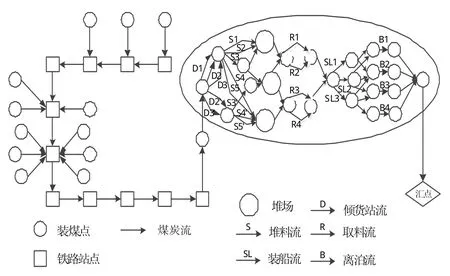
图1 煤炭供应网络
2.2 设施设备维护调度
煤炭供应链设备的预防性维护都有一个维护时间窗,调度维护工作的计划表会对计划期内网络总输出流量产生不同的影响。待维修设备的故障相关关系使得其预防性维护计划必须协调起来制定。因此,煤炭供应链设备维护调度问题可抽象为带边中断动态网络最大流问题,它研究如何调度容量网络边的中断时刻,动态性地分配容量,以最大化计划期内网络的总吞吐量。
3 模型构建及求解
3.1 参数及变量定义
定义[m,n]={m,m+1,...,n},[m]={1,2,...,m},m,n∈Z+。G=(V,A,s,s',C)表示一个网络,其中[V]为节点集合,[A]为网络中弧的集合,s为源点,s'为汇点,[C]为弧容量集合,Ca表示弧a的容量。节点v∈[V],δ-(V)和δ+(V)分别表示进出节点v的弧集。设置网络总时间跨度为T。
网络G中散布着一系列维护作业j∈[J],其中[J]为作业集,作业j∈[J]有一系列属性:处理时间pj∈[T],最早开始维护时间rj∈[T],最迟维护截止时间dj∈[T],作业一旦开始就不能提前终止,在其处理时间段内,与作业j相关联的弧aj上通过的流量为零。[Ja]是弧a上作业集合,假设a上任意两作业的时间窗不重合。作业j∈[J],维护开始时间,sj∈[rj,dj-pj+1]其中[rj,dj-pj+1]称为该作业的维护时间窗,当j∈[Ja],t∈[sj,sj-pj+1]时,弧a的容量在t时刻为零,即当弧a上有作业在处理时,弧a断开,途径a的流量为零。
设置变量:φat为时间t内流经a的流量;xat∈{0,1}表示a是否在时间t内中断,中断为0,否则为1;yjt∈{0,1},j∈[J]表示作业j是否开始于时间t,是则为1,否则为0。
3.2 建立数学模型
目标函数:

约束条件:


目标(1)最大化时间跨度内总流量。约束条件(2)和(3)是流量守恒和容量限制约束,(4)要求每一项设备维护作业j在其时间窗内恰好被完成一次,(5)确保当维护作业j正在处理中时,路径弧a容量为零,(6)是非负约束和0-1约束。
4 BD算法
4.1 BD转化模型
将变量xat与φat分离到两个问题中,分别构成具有调度元素的MP与最大流SP。又因为任一时刻网络最大流仅与该时刻网络各边的中断情况xat有关,因此可以将一段时间内的动态最大流分解为该时间段内每一时刻静态最大流的和,分解后的这类单位时刻静态最大流问题,可以利用线性规划求解器快速求解,这种分解的BD算法能有效提高模型求解效率。
给定xat,t∈[T]的一个可行解为xat,则对∀t∈[T],SP的模型为:

S.t.
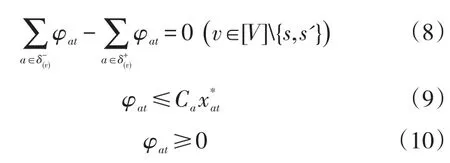

式(11)是加入到MP模型中的割平面。因此以单位时间t划分后的MP模型如下:

S.t.

4.2 求解步骤
BD算法的求解步骤如下:
Step1:初始化。G=(V,A,s,s',C),总时间跨度T,=+∞,=-∞,ε =0.09% ;
Step2:创建空Python字典Y,构建SP和MP的模型;
Step3:初始化 xat=1,∀a∈[A],∀t∈[T],求解SP得到最优解x0、容量约束的对偶变量(ua|a∈[A]),将 xat作为字典Y的键,值为(x0,ua|a∈[A]),在MP中增加约束 θt≤x0,∀t∈[T];
Step4:求解 MP,得新的当前解值、θt及 yjt,;若,转Step5,否则转Step7;
Step5:检索 xat',t'∈[T],如果 xat'是Y的键,取Y中xat'键对应的值(x0,ua|a∈[A]) ,否则,求解SP,将结果置于Y中;
Step6:如果 θt'≥x0,∀t'∈[T],在MP中增加约束θt'≤∑a∈[A]Caxat'uat'(∀t'∈[T]) ;否 则 t'←t'+1 ;若t'=T ,则,转Step4,否则,转Step5;
Step7:算法终止,输出最优解。
5 算例分析
通过数据实验对所设计的BD算法的求解效果进行分析评价。计算实验的标准测试数据来源于文献[7],包括8个规模不一的网络结构、2组可选的维护时间窗口大小不同的数据集,每组数据集中,对应每一个网络结构都有10个单独的实例,那么总共运行的数据实例有160个。通过比较BD算法及Gurobi求解器在1 800s内给出实例的结果来分析算法的优劣。采用Python2.7语言编程,Gurobi6.5建立模型,在Intel Core i7处理器(2.5GHz)、12GB内存的计算机上测试。通过分析BD算法上、下界的gap,运行时间以及算例能被求得最优的个数等指标,分析三种方法的特点,实验结果见表1、表2。

表1 数据集1运行1 800s的结果数据

表2 数据集2运行1 800s的结果数据
观察以上两组实验结果数据,得到如下结论:
(1)通过比较两种算法能求解出实例的平均个数,可知分解算法的求解效率显著高于Gurobi求解器的效率,尤其是在数据集合1中,BD算法得到的最优解的个数在多数网络中更加突出。
(2)在平均gap方面,BD算法与Gurobi求解的结果相差不大,但是在数据集合1中,BD算法表现更好,时间上,在大多数算例中,BD算法消耗的时间成本也较Gurobi更好。结果表明使用Benders分解,将原始模型分割成主问题和子问题的求解技术性能更好。
6 实际案例分析
当前,国内煤炭行业水平方向企业之间的竞争仍然是投资、资源体量之间的竞争。煤矿资源被进一步开发,铁路、煤码头吞吐量的设计呈井喷增长趋势,这些粗放的资源开发与利用行为造成了严重的产能过剩和资源浪费,煤炭行业急需精细的资源管理来提高效率,降低浪费。
一般的,设备维护资源主要是维护工人、维护器具等,维护资源过少会引起维修不及时,而维护资源过多,又增加企业的成本。上文的MaxTFFAO模型假设,任意时刻都有足够的维护资源对设备进行维护,即同一时刻处于维护状态的设备数量不受资源限制,这就需要企业具备足够的维护资源。当资源闲置时,产生浪费。假设G中每条边上散布着数量不等的待维护作业,且每条边上待维护作业的时间窗不重叠,考虑带资源约束的煤炭供应链设备维护计划决策,在MaxTFFAO模型中添加资源约束(17)。

|A|表示G中弧的总数,K是维护资源总数。
煤炭供应链上各环节的设备维护资源类型不同,各环节的维护资源仅仅维护自身环节的设备,如铁轨维修工人检修列车轨道,不会维修码头的堆料机,因此煤炭供应链上各环节维护资源的数量需要分开进行决策。考虑多资源约束,对MaxTFFAO模型进行修正:

其中|Ai|表示G中第i环节边的数量,Ki为第i环节的维护资源数量,i=[q]则表示G中的某一个环节,整个供应链分为q个环节。上述两个模型分别对应于单资源约束与多资源约束的情形。在资源不受限情形下,由MaxTFFAO模型计算网络最大流及最大资源需求量K。随后,在修正后的模型中,逐渐减少K值,网络最大流保持不变,直到K=K1时,网络最大流开始减少;当K继续减少到某一临界值时,修正模型无可行解,此时可推算出最小资源数K2。修正后的模型可找到保持最大流不变情形下的最少资源需求量K1、设备维护作业能及时被处理的最少资源需求量K2以及煤炭供应链设备维护计划表。同理,可求出带约束(18)模型的最少资源需求量组合及设备维护计划表。

表3 单资源约束下数据集1网络1的资源与最大流

表4 多资源约束下数据集1网络1的资源组合与最大流
表3、4给出了文献[7]中数据集合1对应于10组不同维护作业下的网络1在资源受限情形下的网络最大流,可见对于每组维护作业,网络1都有一个最小的维护资源量,使得计划期内的网络最大流达到最大,同时也有最小的维护资源量数使得维护作业能及时得到处理。
7 结论与展望
本文针对煤炭供应链中设备维护计划问题,研究了带边中断动态网络最大流模型及其算法,取得了以下成果:(1)从供应链管理的角度,对设备维护管理展开研究,建模并设计算法求解,对实际煤炭供应链中设备维护作业计划的调度问题有一定的指导意义;(2)详述了BD算法,设计了该算法解决该问题及模型的具体步骤;(3)实验结果表明BD算法是有效的,且在处理大规模网络难题时,能比精确算法更有效提高解的质量。此问题之后的研究方向:(1)考虑具有不确定性因素的“带边中断动态网络最大流”问题,如考虑弧容量随不确定因素改变,利用BD算法设计具有稳健性的作业中断调度表;(2)本文BD算法中,未谈论实验中参数设置的规则,可进一步改进。
[1]宋之杰,陈文静,侯贵宾,等.港口设备维修优化模型及实例研究[J].物流技术,2013,32(9):172-175.
[2]陈文静.基于时间延迟模型的港口设备维修管理研究[D].秦皇岛:燕山大学,2012.
[3]刘艺杰.基于可靠性理论的退化设备预防维修策略研究[D].秦皇岛:燕山大学,2013.
[4]范体军,许淑君,李宏余,等.设备维护外包策略及其对维护计划组织的影响[J].工业工程与管理,2006,11(3):15-18.
[5]崔维伟,陆志强,潘尔顺.基于多目标优化的生产调度与设备维护集成研究[J].计算机集成制造系统,2014,20(6):1 398-1 404.
[6]王红,杜维鑫,刘志龙,等.联合故障与经济相关性的动车组多部件系统维护[J].上海交通大学学报,2016,50(5):660-667.
[7]Boland N,Kalinowski T,Waterer H,et al.Scheduling arc maintenance jobs in a network to maximize total flow over time[J].Discrete Applied Mathematics,2014,163(1):34-52.
[8]Boland N,Kalinowski T,Kapoor R,et al.Scheduling unit processing time arc shutdown jobs to maximize network flow over time:complexity results[J].Computer Science,2013,63(2):196-202.
[9]J F Benders.Partitioning procedures for solving mixed-variables programming problems[J].Computational Management Science,2005,2(1):3-19.
[10]Fischetti Lodi.Local branching[J].Mathematical Programming,2003,98(1):23-47.
