基于“反学习”理论的人工蜂群算法在订单分批问题中的应用

吴天行，郭 键

（北京物资学院，北京 101149）

1 引言

当今社会市场竞争日益严重，企业生产的产品差异化程度日渐降低，如何提高企业的竞争优势以保证企业在市场竞争中占得先机已经成为许多企业考虑的重点[1]，物流作为“第三利润源”的概念由此而生。为了优化物流系统，降低物流成本，目前众多学者将如何提高物流系统的效率作为研究的重点内容。

纵观企业整个物流系统，配送和仓储在物流系统中占据了很大的比重，而相关研究表明，仓储与配送作业的成本在物流总成本中占据40%以上的比重[2]。而在仓储和配送作业中，人工拣选作业中的拣选行走成本比例最大，如何优化拣选作业，缩短拣选作业的行走距离已经成为当前优化物流系统的当务之急。订单分批策略是现今优化拣选作业研究的一个热点问题。该问题最早可以追溯至Van den berg[3]在上世纪90年代发表的关于优化仓储作业的论文中，在文中该学者认为将订单分成批次集中拣选可以有效的缩短拣选作业的路径，提高拣选作业效率。

2 订单分批模型的建立

传统意义上订单的拣选作业是按照先到先服务的原则进行的，即对订单按照到达的时间先后顺序进行拣选[4]，这种方法一般不会刻意对订单进行分批，因此一般也不需要建立特定的模型进行研究。但是随着订单数量的增加，先到先服务的模式越来越难以满足拣选作业的高效要求，这时如何快速高效拣选订单就成为了研究的方向。

订单分批问题就是利用数学优化方法，首先是建立需要求解的目标函数，其次是根据问题的具体情况对限制性约束加以确定，最后在确定目标函数和限制性条件的基础上，利用智能算法求解建立的数学模型，得到模型的最优解，完成整个优化过程。

2.1 模型建立的背景

现在某企业有一个单区型仓库，该仓库的基本布局如图1所示。每天都会有一定数量的订单到达仓库，这时就需要对仓库内的货品按照到达的订单进行拣选。

图1 仓库基本布局图

根据该单区型仓库的实际情况，设定整个仓库由A排货架组成，每一排货架的货位数量是B，每一个货位的长度和宽度都为C，仓库内拣选通道的宽度为D，仓库的左下角有一个出入口，所有拣选完的订单都由左下角的出入口送出仓库。拣选设备是仓库中常见的拣选车，每一排拣选通道只能容纳一辆拣选车，即不存在两辆拣选车在一个通道内拣选的情况。为了方便说明和计算，订单分批模型不考虑“紧急插单”、订单拆分和商品缺货的情况。每一个订单内的货品重量和体积都为E。

2.2 分批模型的构建

根据上文做出的相关假设，下面将会建立订单分批模型。

目标函数：

约束条件：

根据以上函数，下面将会对分批模型中涉及到的符号进行说明，见表1。

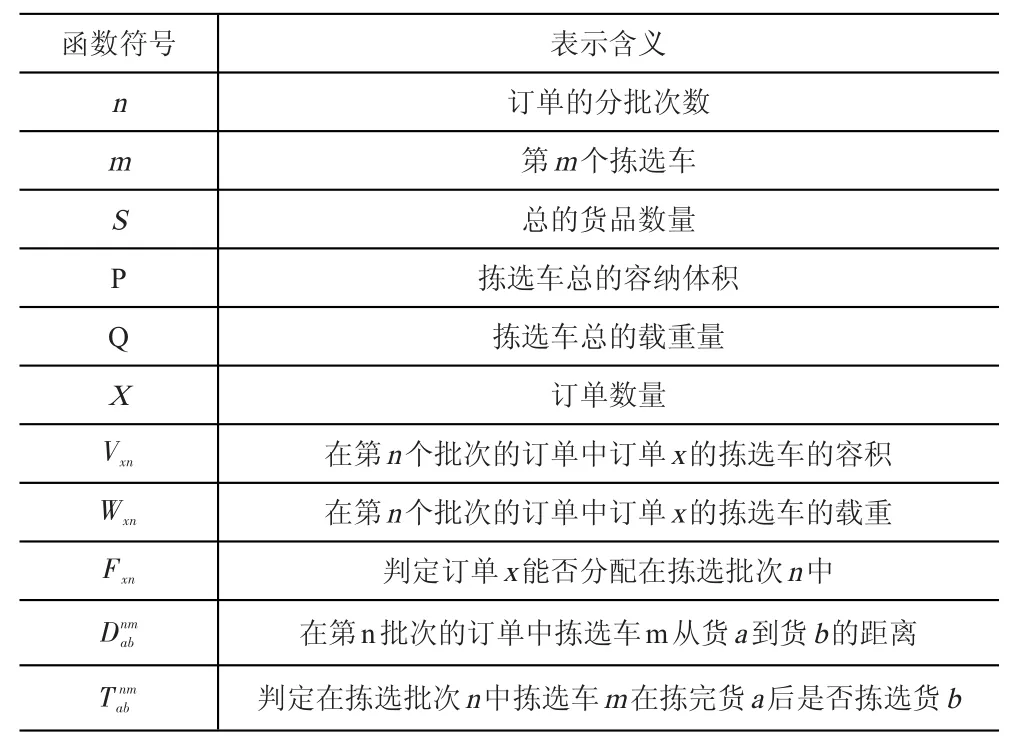
表1 函数符号说明

下面将会对分批模型中的每一个公式的含义进行阐述。式（1）表示在对所有的订单分批以后，总的拣选路径是最短的。式（2）表示每一批订单的体积不超过拣选车的容积。式（3）表示每一批订单的重量不超过拣选车的载重量。式（4）表示需要拣选的订单只可以在一个批次中，即订单不可以被分割。式（5）表示货物a、b是否为连续拣选，即拣完货a后是否立即拣选货b。

3 人工蜂群算法与“反学习”理论

3.1 人工蜂群算法概述

人工蜂群算法（Artificial Bee Colony）是2005年由土耳其学者Karaboga[5]提出的，该算法的核心思想是模仿蜜蜂之间的相互协作、共同完成采集蜂蜜的觅食行为。人工蜂群算法主要有四个要素，分别是蜂源、引领蜂、跟随蜂和侦查蜂[6]。另外整个搜索过程还包括召集蜜蜂和蜜源的放弃两种基本行为[7]。

为了更为方便的描述整个蜂群算法的过程，下面将会用数学语言对整个算法进行详细的阐述。

（1）初始解的生成。随机生成数量为N的初始种群P，种群的规模表示为N，种群中的每一个解表示为Xi，每一个Xi都是种群中的一个D维向量，生成解按照式（6）来生成。

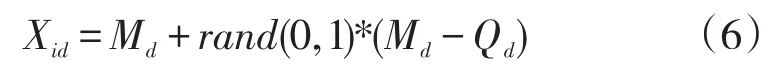
式（6）中，Xid表示第i个解的第d维，Md和Qd分别表示为搜索区域的上限和下限，d=1,2,...,D。

（2）产生新的蜂源。在搜索的早期阶段，引领蜂需要根据式（7）生成新的蜜源来进行搜索。

式（7）中d是[1,D]中的一个随机整数，含义是引领蜂随机选择一个维度进行搜索，j=1,2，...，j≠ i，表示在蜂源中随机选择一个蜂源i且不与j相同。φ是一个在[-1,1]上均匀分布的随机数。采用贪心算法的方式保留所有的适应度值高的蜂源Vi。

（3）计算需要跟随的概率。跟随蜂从引领蜂获得蜜源的信息，依据式（8）计算得到概率并进行跟随。

跟随蜂随机的选择引领蜂，在[0,1]之间产生一个随机数r，如果Pi＞r，则根据式（7）产生新的蜂源，并且依照贪心算法来确定是否对蜂源进行保留。

在搜索过程中，如果在多次迭代以后，依然没有找到更好的蜂源，则抛弃现有蜂源，利用式（9）来产生新的蜂源。

（4）评价解的适应度。为了保证获得的解具有一般性，引入适应度的概念，按照式（10）对得到的解的适应度进行评价。

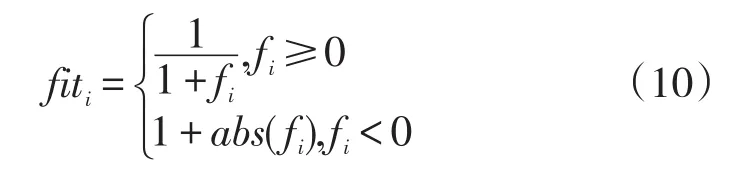
式（10）中fi为函数值，i=1,2,....,N。

3.2 基于“反学习”理论的初始种群构成

在基本的人工蜂群算法中，按照随机的方式生成初始种群，这就必然使得随机生成的初始种群在解的空间内的分布是不均匀的，而这种方式无疑会限制算法的求解效率，因此为了增强初始解的多样性，提高算法效率，现将“反向解”的概念引入到初始种群的构建中。

“反学习”理论的核心思想就是综合考虑当前解和反向解距离最优解的距离，这样就可以最大程度上提高算法的寻优速度和收敛速度[8]。“反学习”理论不仅可以应用在算法早期的初始种群生成阶段，还可以使用在算法的迭代过程中。在每一次的迭代中，可以在生成初始解的基础上再生成与之相对应的一组“反向解”，进而提高算法在每一次迭代的效率。下面将以数学语言的方式阐述“反向解”生成的主要过程。

（1）产生初始解。初始解的产生可以参照式（6）来进行。利用式（6）可以产生数量为N的初始解构成初始种群。

（2）产生反向解。反向解的产生依据式（11）来进行。根据式（11）可以产生数量同样为N的反向解，构成初始种群。

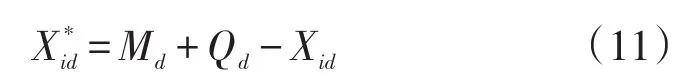
（3）计算适应度并进行比较。根据式（10）计算“正向解”Xid和“反向解”的适应度值，并且进行大小的比较，选择适应度较高的解构成初始种群。

4 分批算法的仿真验证

4.1 仿真验证背景

为了验证算法的有效性，本文将在单区型仓库下随机生成一批订单，使用本文提出的分批算法和两种传统分批算法进行仿真应用，从而验证基于“反学习”理论的蜂群算法在订单分批问题中的科学性和有效性。

现在根据单区型仓库的特点，设定仓库通道宽度为2，每一个货位的宽度为1，仓库由16排、每排为15个货位的货架组成，拣选车最大容积和载重量都为20个单位，每一个需要拣选的货品的重量和体积都为1个单位，现在随机生成了8张订单需要拣选，到达的订单具体的商品品项的分布如图2所示。

图2 订单商品品项分布图

4.2 两种传统的分批算法

为了便于比较验证，本文选取了两种传统的订单分批算法进行分批，这两种算法分别为基于通道相似性的分批算法和基于图论的分批算法。

基于通道相似性的算法核心思想就是“分布在同一通道内的商品一般情况下拣选的距离较短[9]”。基本步骤是首先找到在相同或者相似的通道内的订单，然后通过判断是否满足分批模型的约束条件来确定哪些订单划分为一个拣选批次。

利用该算法进行分批，最重要的就是要得到通道的相似性以及建立订单分批规则，为了方便说明和计算，通道相似的公式和订单分批规则就使用李诗珍在文献中创建的公式与规则，分批后的结果见表2。

表2 基于相似性的分批结果

基于图论的订单分批算法的核心思想是从一个货品出发直接寻找距离该商品最短的商品进行聚类，再根据分批规则进行分批，该算法是文献[10]中使用的一种订单分批方法。具体过程为首先将每一个货品进行编号并计算距离矩阵；其次利用广度优先搜索算法建立聚类邻接矩阵；最后根据订单分批规则进行分批。为了便于计算和说明，按照文献[10]建立的规则进行分批，具体的分批结果见表3。

表3 基于图论的分批结果

4.3 基于“反学习”理论的分批算法

根据前文的叙述和单区型仓库的相关数据，下面将会使用本文提出的基于“反学习”理论的人工蜂群算法对订单内的货品进行分批，利用MATLAB软件设定算法的迭代次数为1 000次，在内存为16G的Windows系统中运行，可以得到最后的分批结果，见表4。

表4 基于“反学习”理论的蜂群算法分批结果

人工蜂群算法的运行结果如图3所示。

图3 人工蜂群算法运行结果

4.4 结果分析

根据之前不同算法的分批结果，下面将各个算法的分批结果整理汇总，见表5。

表5 各分批算法结果对比

根据表5可以清楚地看到，基于“反学习”理论的人工蜂群算法的分批结果最优，与基于相似性和基于图论的分批算法相比，在拣选距离上分别缩短了35.9%和33.5%，并且根据图3可知，在算法迭代到430次左右时已经找到了最优解，算法的搜索效率较高。

从人工蜂群算法原理的角度分析可知，利用人工蜂群算法进行分批是基于订单中每一个货品的角度寻找最优解，这样进行分批往往比基于通道相似性的分批算法得到的结果更为精确，同时由于人工蜂群算法的收敛速度较快，利用该算法进行分批在时间上相较于基于图论的聚类算法更有优势。为了弥补算法早期容易陷入局部最优解的缺点，本文尝试引入了“反学习”理论，对人工蜂群算法在初始种群和迭代的初始解生成阶段进行优化，从分批的结果来看，优化的效果较优。

5 结语

根据上文的分批结果可以知道，采用基于“反学习”理论的人工蜂群算法对订单进行分批，可以获得较好的分批结果，在第4节仿真验证中，采用该算法对订单进行分批相较于两种传统的分批算法在拣选路径的距离上，分别缩短了35.9%和33.5%，在拣选距离的缩短上有较大的提升。

针对现在人工拣选效率较低的问题，本文尝试应用订单分批策略对拣选作业进行优化，根据单区型仓库的特点，提出了基于人工蜂群算法的订单分批方法，并且针对蜂群算法的缺陷，将“反学习”理论融合到蜂群算法中，通过仿真实验对该算法和传统的两种分批算法进行分批验证，根据分批结果认为，利用基于“反学习”理论的人工蜂群算法对订单进行分批，无论是在分批时间上还是在拣选的距离上，都要优于传统的订单分批算法，利用该算法在单区型仓库中进行分批拣选具有一定的推广意义。

[1]白冬.现代企业管理模式的改革与发展[J].企业技术开发,2014,(14).

[2]李伊松.物流成本管理[M].北京:清华大学出版社,2005.

[3]刘志帅.YB公司天津分公司仓库货位优化问题研究[D].天津:河北工业大学,2013.

[4]韩玉芳.配送中心订单分批问题研究[D].济南:山东大学,2015.

[5]Karabogad.An idea based on honey bee swarm for numerical optimization Computers Engineering Department[D].Engineering Faculty Erciyes University,2005．

[6]李艳娟.基于禁忌搜索的人工蜂群算法[J].计算机工程与应用,2017,(4).

[7]郝继升.改进的人工蜂群算法[J].江西科学,2017,(2).

[8]秦全德.人工蜂群算法研究综述[J].智能系统学报,2014,(2).

[9]李诗珍.配送中心订单分批拣货模型及种籽启发式算法[J].起重运输机械,2009,(1).

[10]吴天行.基于图论的聚类算法在订单分批问题中的应用[J].物流技术,2017,(8).