航空发动机双转子系统碰摩故障的仿真研究

金业壮， 王德友， 闻邦椿

(1.东北大学 机械工程与自动化学院， 辽宁 沈阳 110819； 2.沈阳航空航天大学 航空航天工程学部，辽宁 沈阳 110136； 3.中国航空工业集团公司 沈阳发动机设计研究所，辽宁 沈阳 110015)

在航空发动机的研制过程中，人们为了提高其推重比及其结构效率，不断缩小发动机的转、静子间隙，与此同时，转子质量的不平衡、转子与静子的不对中、高温膨胀等因素也会导致转子系统振动大于转、静子间隙，进而引发大量的碰摩问题。根据资料统计，由碰摩故障引发的航空发动机转子系统运动失稳、轴系破坏、叶片折断直至机械失效等事故日益突出，在近年来我国航空发动机的重大事故中，有30%是由碰摩故障而引起的直接或间接振动故障所导致[1-2]，该类型故障的特殊性和复杂性也日益受到国内外学者的关注。

国外，Childs[3]研究了碰摩转子的拟周期现象，研究发现在碰摩转子中，倍周期的分叉进入到混动区域是必然的，同时还发现了稳定区域范围会随着系统的参数变化而发生改变。Muszynska[4]基于动量守恒定律研究了系统的碰摩问题，并建立了一个较为完备的关于约束微分系统的碰摩力学模型。同时，在上述模型中引入了弹性恢复系统，用来表示碰摩时能量的损失，提出了对模型进行完善的方法[5]。Beatty[6]提出了一种通过分段线形刚度表示碰摩力的数学模型，并基于谐波响应实验数据，确定了良性接触与故障初期不稳定接触之间的界限。Adams等[7]提出了一种数值仿真分析方法，并研究了转子系统的转速、不平衡量和径向间隙对碰摩系统动力学特性的影响和规律。Piccoli等[8]提出了一种识别混沌运动的测试方法，并测试获得了庞加莱图、混沌相图、李雅普诺夫指数等参数。同时，还将转子和定子的偏心旋转影响引入到Jeffcott转子系统的碰摩模型中，研究了混沌运动对转子系统运动稳定性的影响。Groll等[9]提出了一种基于谐波平衡法的数值算法，用以计算在周期激励下一个非线性转/定子接触系统的周期响应。Popprath等[10]描述了一种与定子有间歇性接触的Jeffcott转子，其中的定子模型可作为一个附加的振动系统，并与转子模型通过非线性接触力相互作用。Banakh等[11]研究了转子和浮动密封圈之间的振动和冲击影响，还考虑了转子和密封圈间隙之间的水动力以及密封圈和外壳之间的干摩擦。

国内，褚福磊等[12]讨论了转子系统的转速及不平衡量的变化对碰摩转子系统的振动特性的影响，并建立了一个由油膜轴承支撑的碰摩转子动力学模型。王德友[13]总结了旋转机械中，转、静子碰摩时的振动特性，并且指出碰摩故障是其他故障(如不平衡、偏心、干摩擦等)造成的二次效应，并且碰摩故障还会使结构的振动幅值大幅增加。戴兴建等[14]考虑了限位器的碰摩，建立了碰摩转子系统的动力学方程，模型中对碰摩力采用了分段线弹性以及库伦摩擦模型的描述方法，对系统中的双频进动、局部碰摩、整圈碰摩以及拟整圈碰摩时的振动特性进行了研究。单颖春等[15]针对现有的模型碰摩力模型存在的问题，首先应用ANSYS软件中的接触分析，计算了转静子间的非线性接触刚度，获得非线性碰摩力模型。同时，还利用时域波形、频谱分析和小波变换对响应进行了分析，得出相关的碰摩故障特征。何田等[15]建立了双转子碰摩系统的动力学方程，利用分叉图、相图、Poincaré图等从时域研究了高、低速转子随转速变化时显示的周期、拟周期和混沌等复杂动力学现象及其变化规律。

虽然目前对航空发动机碰摩故障问题进行了大量研究，并取得了阶段性的研究成果，但主要是集中在单转子碰摩问题上。本文以某型号航空发动机的双转子模型实验台为研究对象，在合理简化的基础上，基于ADAMS多体动力学仿真软件，建立了双转子碰摩系统的动力学模型，同时对其动力学特性进行了仿真研究。

1 双转子碰摩系统ADAMS模型

1.1 多体系统的动力学原理

在ADAMS中，可根据多体动力学相关理论，建立系统的拉格朗日运动方程。对于每个刚体，可列出6个广义坐标，且根据带乘子的拉格朗日方程，获得相应的约束方程[17]：

(1)

ψi=0 (i=1,2,…，m)

(2)

式中：K为系统动能，qj描述系统的广义坐标，ψi为统的约束方程，Fj为在广义坐标方向的广义力，λj为m×1的拉格朗日乘子列阵。

物体Bi(i=1,2,…,N)的动能可表示为

(3)

ADAMS中柔性体模块是基于弹性小变形假设建立的。其基本思想是赋予柔性体一个模态集，采用模态展开法，利用模态坐标来表示弹性位移。通过计算每一时刻物体的弹性位移来描述其变形运动。设柔性体的模态坐标是qf={q1,q2,…,qn}T，则柔性体的广义坐标可表示为

ri=x+A(Si+φiqf)

(4)

式中：x为从整体坐标系原点到局部坐标系原点的位置矢量，A为局部坐标系相对整体坐标系的方向余弦矩阵，Si为i点在未变形时在局部坐标系的位置，φi为点i的移动自由度的模态矩阵子块。

物体Bi(刚-柔系统)上任一点i在整体坐标系的位置向量可以表示为

(5)

刚-柔系统的动能可以表示为

(6)

式中：mi为结点i的模态质量，Ii为结点i的模态惯量，ω为物体坐标系的角速度向量。

(7)

令重力势能的参考点为惯性基的坐标原点，物体Bi的重力势能为

(8)

式中g为重力在惯性基中的坐标阵。

(9)

(10)

式中：|d|-|d0|为力元的变形，|d0|为弹簧原长。

由式(1)、(2)可以获得刚/柔混合体的动力学微分-代数方程。对于这种代数-微分方程的求解方法有多种，如可将二阶微分方程降阶为一阶微分方程来求解，或直接对二阶微分方程进行积分求解，ADAMS就采用了前一种方法。

1.2 双转子碰摩系统ADAMS模型的建立

航空发动机转子结构中，多数为双转子结构，因此在转、静件发生碰摩时，由于碰摩力的非线性作用，其振动响应的特征与单转子系统对应的振动响应特征有着非常明显的差别。针对如图1所示的双转子碰摩试验系统，建立了双转子碰摩的多体动力学模型，其中，系统的弹性模量E为2.09×1011Pa，泊松比υ为0.295，密度ρ为7.87×103kg/m3，转子系统的基本参数如表1所示。

图1 双转子碰摩系统结构简图Fig.1 Structure diagram of the double-rotor rubbing system

进行转子系统建模时，采取如下简化处理：1)两端弹性支承结构相同，将其均视为线性，支承刚度由轴承刚度和鼠笼结构刚度串联得到，分别在横向水平和垂直方向上，采用“spring”模拟支承，刚度、阻尼设置同表1计算值；2)转动约束为理想约束；3)转轴视为刚体，不考虑转轴变形对动力学特性的影响；4)通过在高、低压转盘上各附加一质量块来模拟双转子不平衡；5)在距离低压转盘一定间隙处设置碰摩板，通过调整间隙、碰摩参数来模拟不同碰摩工况。

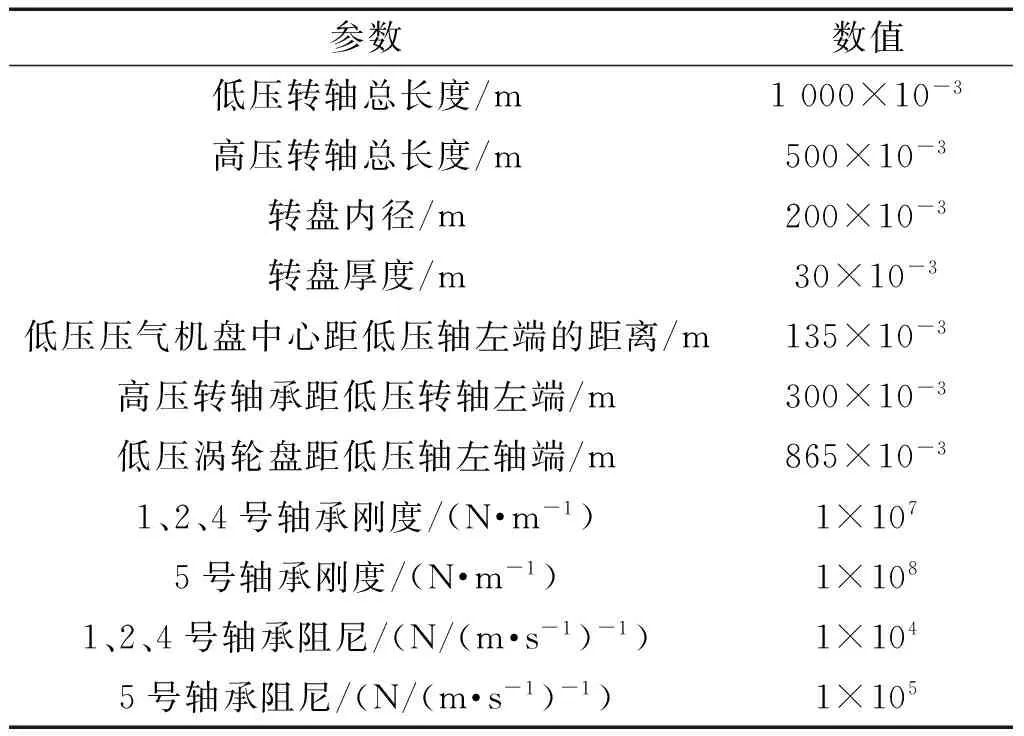
表1 转子系统基本参数

在建立转子系统几何模型的基础上，定义材料属性、合理设置约束与载荷，具体建模过程为：1)将转轴、转盘的材料参数根据材料属性进行设置；2)低压转子系统两端用“spring”单元来模拟轴承，施加在两端支承位置与大地之间；在输入轴支承处施加绕x轴旋转的点驱动；3)高压转子系统两端用“spring”单元来模拟轴承，一端施加在支承位置与大地之间；另一端施加在支承位置与转轴之间；4)动力学模型校对，设置好约束与载荷后，利用“Model Verify”对模型约束检查，以确保模型的正确性。最终建立的ADAMS双转子碰磨多体动力学模型如图2所示。

1.低压转子左支承, 2.不平衡质量1, 3.低压盘, 4.碰磨块, 5.轴,6.高压转子左支承, 7.不平衡质量2, 8.高压盘, 9.高压转子轴,10.高压转子右支承, 11.低压转子右支承。图2 基于ADAMS的双转子碰摩系统多体动力学模型Fig.2 Multi-body dynamics model of the double-rotor rubbing system based on ADAMS

2 双转子碰摩系统ADAMS模型分析

根据1.2节建立的模型，模拟实际工况进行仿真，初始不平衡量1 500 g·mm，转速3 000 r/min (50 Hz)，初始碰摩参数如表2所示。通过调整碰摩参数，模拟不同的碰摩状态，进行碰摩响应仿真分析。

首先，通过选取不同碰摩刚度104、106和108N/m模拟双转子轻微、较重和严重碰摩工况，其对应碰摩阻尼分别为10、100和1 000 N·s/m。获得三种状态下低压转盘中心的时域、频域和轨迹分别如图3～5所示。

表2双转子碰摩系统初始参数设置

Table2Theinitialparametersettingsofthedouble-rotorrubbingsystem

参数数值碰摩间隙/m10-5碰摩刚度/(N·m-1)104碰摩阻尼系数/(N·(m·s-1)-1)100非线性力指数1.5渗透深度/m10-3静摩擦系数0.3动摩擦系数0.1

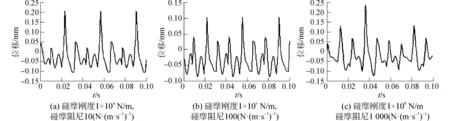
图3 不同碰摩刚度下双转子碰摩系统转盘中心的位移时域Fig.3 The measured waveform of rotary center of double-rotor rubbing system under different rubbing stiffness

图4 不同碰摩刚度下双转子碰摩系统转盘中心的位移频域Fig.4 The spectrum of rotary center of double-rotor rubbing system under different rubbing stiffness

图5 不同碰摩刚度下双转子碰摩系统转盘中心的轴心轨迹Fig.5 The axle center obit of rotary center of double-rotor rubbing system under different rubbing stiffness

由图3～5可以看出，随着碰摩刚度以及阻尼系数的增加，振动响应的频谱变得越来越复杂，出现了高次谐波、组合谐波和次谐波成分，倍频频率成分越来越丰富。当碰摩刚度以及阻尼较大时，碰摩对于系统的振动响应影响越大，进而加剧碰摩。

为了研究不同刚度和阻尼对转子系统碰摩力的影响，图6给出了不同碰摩刚度条件下的碰摩力。对碰摩力的变化趋势进行分析可知，随着碰摩刚度的增大，碰摩力将随着增大，进而加剧了碰摩程度。

图6 双转子碰摩系统不同碰摩刚度条件下的碰摩力Fig.6 Rubbing force of double-rotor rubbing system under different rubbing stiffness conditions

3 结论

1)通过对碰摩转子系统多体动力学模型进行仿真分析可知，在转静件碰摩从轻到重的整个过程中，其振动频谱成分与碰摩参数有着密切的关系。

2)随着碰摩刚度以及阻尼系数的增加，振动响应的频谱变得越来越复杂，出现了高次谐波、组合谐波和次谐波成分。

3)当碰摩刚度和阻尼系数较大时，随着碰摩刚度的增大，碰摩力将随着增大，进而加剧碰摩。

[1] 晏砺堂．航空燃气轮机振动和减振[M]．北京：国防工业出版社， 1991．

YAN Litang. Aero-gas turbine vibration and vibration reduction[M]．Beijing: National Defence of Industry Press,1991.

[2] 吴大观．探讨我国航空发动机发展中出现的问题[J]．燃气涡轮试验与研究, 2010, 13(4): 1-4．

WU Daguan. The discussion of the problems of aviation engine development in China[J]．Gas turbine experiment and research, 2010, 13(4): 1-4．

[3] CHILDS D W. Fractional-frequency rotor motion due to nonsymmetric clearance effects[J]. Journal of engineering for gas turbines and power, 1982, 104(3): 533-541.

[4] MUSZYNSKA A. Rub-an important malfunction in rotating machinery[C]//Proceedings of the Senior Mechanical Engineering Seminar, Carson City Nevada, 1983: 61-66.

[5] MUSZYNSKA A. Rotor-to-stationary element rub-related vibration phenomena in rotating machinery-literature survey [J]. The shock and vibration digest, 1989, 21(3)： 3-11.

[6] BEATTY R F. Differentiating rotor response due to radial rubbing [J]. Journal of vibration, acoustics, stress, and reliability in design, 1985, 107： 151-160.

[7] ADAMS M L, ABU-MAHFOUZ I A. Exploratory research on chaos concepts as diagnostic tools for assessing rotating machinery vibration signatures[C]//Proceedings of the IFToMM Fourth International Conference on Rotor Dynamics. [S.l.]: 1994: 7-9.

[8] PICCOLI H C, WEBER H I. Experimental observation of chaotic motion in a rotor with rubbing[J]. Nonlinear dynamics, 1998, 16(1): 55-70.

[9] Von GROLL G,EWINS D J.The harmonic balance method with arc-length continuation in rotor/stator contact problems [J]. Journal of sound and vibration, 2001, 241(2): 223-233.

[10] POPPRATH S, ECKER H. Nonlinear dynamics of a rotor contacting an elastically suspended stator[J]. Journal of sound and vibration, 2007, 308(3): 767-784.

[11] BANAKH L, NIKIFOROV A. Vibroimpact regimes and stability of system “Rotor—Sealing Ring”[J]. Journal of sound and vibration, 2007, 308(3): 785-793.

[12] 褚福磊, 张正松, 冯冠平. 碰摩转子系统的混沌特性[J].清华大学学报，1996, 36(6): 52-57.

CHU Fulei, ZHANG Zhengsong, FENG Guanping. Chaotic behavior of a rub rotor model[J]. Journal of Tsinghua University, 1996, 36(6): 52-57.

[13] 王德友. 旋转机械转静子碰摩振动特性[J]. 航空发动机, 1998(2): 37-41.

WANG Deyou. Effects of rubbing on the rotor-stator of rotating machinery[J]. Aeroengine, 1998(2): 37-41.

[14] 戴兴建，董金平,张小章. 不平衡量对转子碰摩振动的影响[J].机械工程学报， 2001, 137(6): 90-98.

DAI Xingjian, DONG Jinping, ZHANG Xiaozhang. Effects of unbalances on the rotor/stop rubbing[J]. Chinese journal of mechanical engineering, 2001, 137(6): 90-98.

[15] 单颖春, 刘献栋, 何田, 等. 双转子系统碰摩有限元接触分析模型及故障诊断[J]. 航空动力学报, 2006, 20(5): 789-794.

SHAN Chunying, LIU Xiandong, HE Tian, et al. Research on the finite element impact-contact analytical model of dual-rotor system and its diagnosis method[J]. Journal of aerospace power, 2006, 20(5): 789-794.

[16] 何田, 刘献栋, 李其汉, 等. 转-转碰摩双转子系统的非线性特性研究[C]//全国非线性动力学和运动稳定性学术会议. 2007: 23-28.

HE Tian, LIU Xiandong, LI Qihan, et al. Nonlinear characteristics of a dual-rotor system with rotor-rotor rubbing[C]//National Conference on Nonlinear Dynamics and Motion Stability. 2007: 23-28.

[17] 李增刚. ADAMS入门详解与实例[M].北京：国防工业出版社, 2006： 125-172.

LI Zenggang. Introduction to ADAMS for details and examples[M]. Beijing: National Defence of Industry Press, 2006： 125-172.

本文引用格式：

金业壮， 王德友， 闻邦椿. 航空发动机双转子系统碰摩故障的仿真研究[J]. 哈尔滨工程大学学报， 2017， 38(12): 1872-1876, 1914.

JIN Yezhuang, WANG Deyou, WEN Bangchun. Dynamic simulation on double-rotor system of aeroengine with rubbing fault[J]. Journal of Harbin Engineering University， 2017， 38(12): 1872-1876, 1914.