水力旋流器旋流运动的格子Boltzmann模拟
2018-01-15胡亮朱卫兵张小彬
胡亮, 朱卫兵, 张小彬
(哈尔滨工程大学 航天与建筑工程学院,黑龙江 哈尔滨 150001)
利用离心力将两相分离在工程中已被广泛采用,如旋风除尘器、石油工业气液旋流器和航空发动机动压式油气分离器等[1-2]。根据气液主相不同,通常称为旋风分离器和水力旋流器。
Erdal、Hreiz等[3-5]通过实验探讨了结构参数对水力旋流器流场的影响,结果表明入口结构及数量对流场分布均有较大影响。Junwei Yang等[6]建立了水力旋流器液相停留时间预测模型。研究表明,水力旋流器内部流动复杂,存在三维强旋湍流运动,且轴向存在二次流扰动。在数值模拟方面,Hreiz等[7]利用Fluent中几种湍流模型系统模拟了水力旋流器内的旋流场,发现Realizableκ-ε模型和LES模型对于流场细节的捕捉还不够准确,需要更有效的数值方法。格子Boltzmann方法(lattice Boltzmann method,LBM)能够真实的反映流体粒子间的相互作用,并提高流场的计算精度[8],具有描述流场局部二次流现象的潜力,而这类问题的研究可以加深对水力旋流器的理论认识,为水力旋流器的研制提供理论依据;针对三维流动问题,LBM演化方程为显式方程,无需迭代计算,在非稳态计算中效率很高;同时LBM具有易并行的优点。Derksen等[9-11]采用LBM对旋风分离器气相旋流场进行研究,准确描述了旋涡中心的旋进涡核(precessing vortex core,PVC)现象,即旋进涡核现象。上述研究表明,LBM已成功应用在旋风分离器的流场分析中。与旋风分离器相比,由于主相和壁面影响的不同,水力旋流器的流场存在更大的非轴对称性[12],且流场中心的二次回流区域也有明显差异[7]。
Bhanjee等[13]探讨了LBM在水力旋流器模拟中的应用方法,结果表明LBM给出的旋流场流动趋势与以往认知一致,但未对计算结果做出进一步定量分析。本文以文献[12]的实验数据为基础,进一步探讨LBM在水力旋流器中的应用,通过流场描述、定量分析及对旋进涡核现象模拟等,深入了解LBM在此问题上的应用前景。
1 Boltzmann模型
1.1 格子Boltzmann方法
本文采用D3Q19单松弛格子Boltzmann模型进行数值模拟,其演化方程即含外力项的格子Boltzmann-BGK方程如下
fi(r+eiδt,t+δt)-fi(r,t)=δtFi(r,t)-
(1)
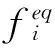
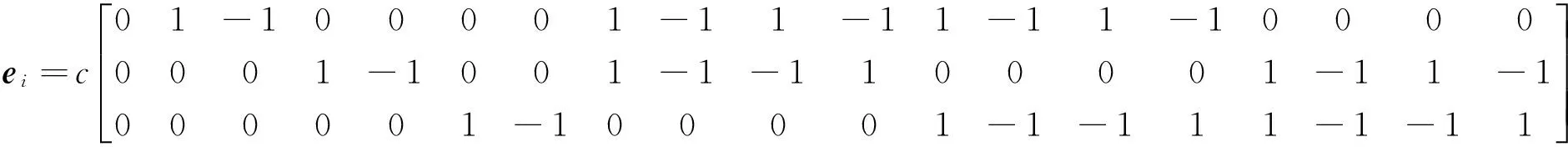
(2)
式中:c=δx/δt,δx、δt分别为网格步长和时间步长。
宏观密度和速度分别为
(3)
(4)
式中:cs为格子声速,ωi为权函数:ωi=1/3(i为原点位置),ωi=1/18(i为6个坐标轴方向),ωi=1/36(i为12个对角线方向)。
1.2 湍流模型
palabos中湍流模型采用LES中的标准Smagorinsky模型,式(1)中的无量纲弛豫时间τ计算公式为
(5)
(6)
式中:cs=0.14,S为应变率张量。
2 物理模型及网格无关性验证
2.1 物理模型
采用文献[12]的实验模型,模型结构与参数如图1所示。本文获取的平均速度分布截面位置均在图中实验测试平面上,如图1所示。
根据文献[12]提供的数据,模拟选择了四种不同实验条件,参数如表1所示。表中,ν为流体运动粘度,Q为流体体积流量,Uav为分离器筒体平均轴向速度。本文采用速度入口边界条件,出口为自由出流,壁面边界采用具有二阶精度的Guo格式非平衡外推边界。
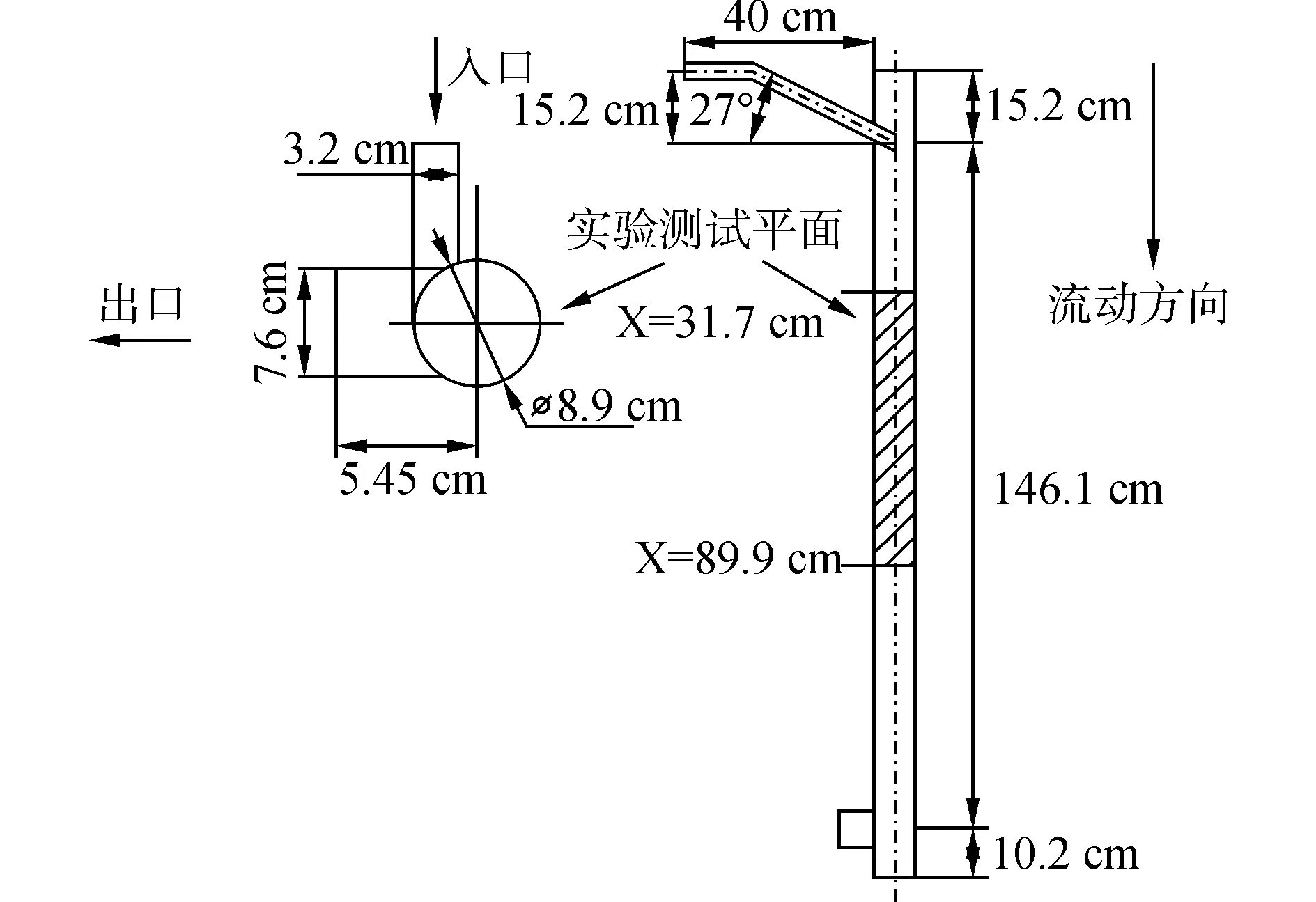
图1 物理模型Fig.1 Geometry model

工况ν×106/(m2·s-1)Q/(m3·s-1)Uav/(m·s-1)Re170.000680.1091514270.003390.5457570310.000630.1029285410.004540.73166855
2.2 网格无关性验证
由于采用palabos中的分块网格技术,计算网格量统计只涉及流体域相关的网格。本文选取三种网格模型对工况3进行计算,并对截面X=31.7 cm处的平均切向速度分布进行对比,对比结果如图2所示。其中速度值进行了无量纲处理,下文处理方式一致,不再赘述。
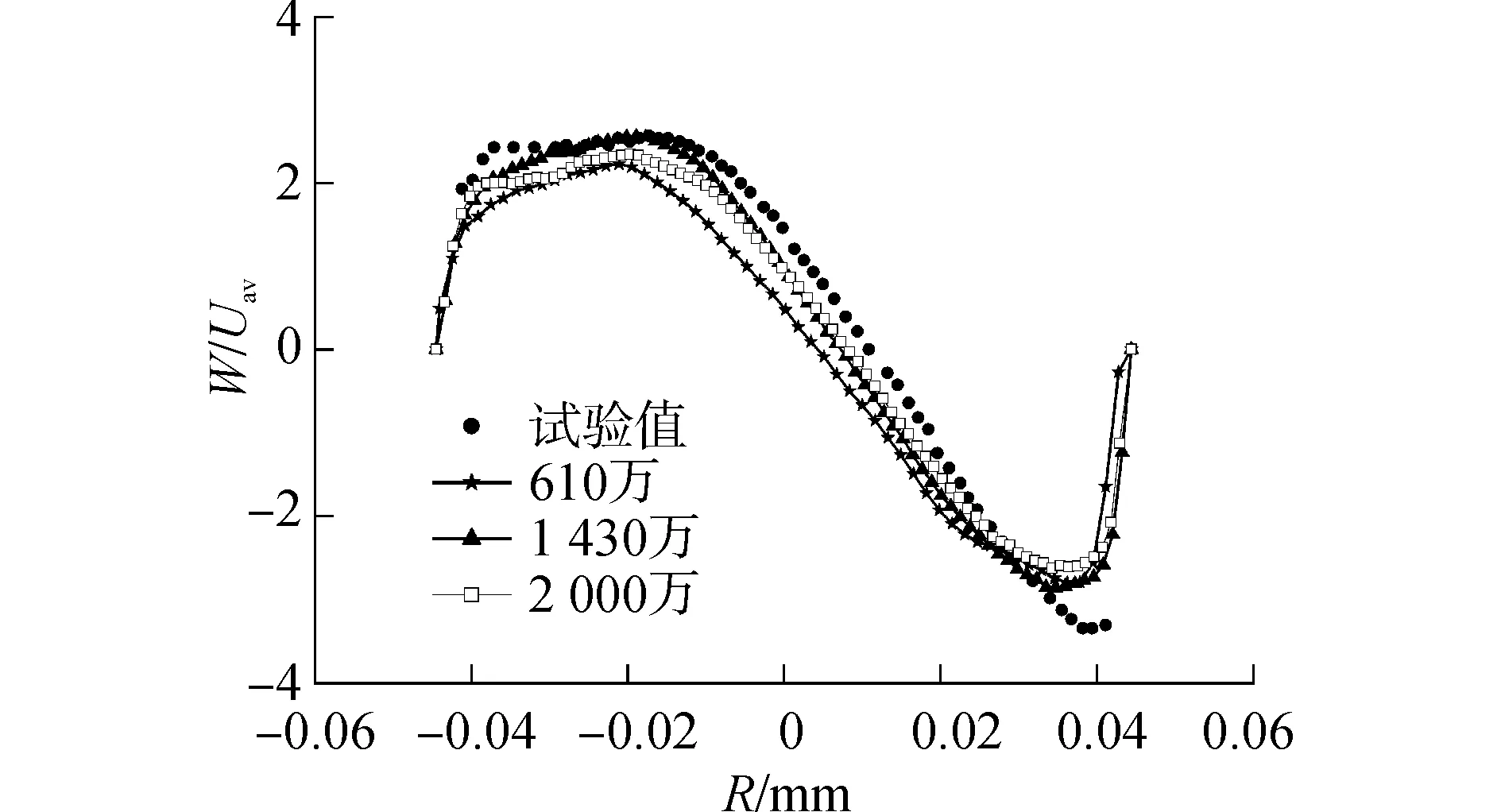
图2 截面X=31.7 cm处平均切向速度分布Fig.2 Average tangential velocity profiles at X=31.7 cm
经过对比,1 430万和2 000万网格量的模型计算结果比较接近,最大相差8.4%。考虑到计算时长的影响,本文研究选择1 430万网格量的计算模型,其中计算网格步长δx=1.2 mm,时间步长δt=6.23×10-5s。计算在Intel core i7 4770处理器上进行,CPU主频为3.40 GHz、内存16 G、8核并行,每个工况计算时长约100 h。
3 水力旋流器疏场研究与分析
水力旋流器存在复杂的三维强旋湍流运动,其主要体现为各分向速度分布以及旋涡形状变化;其中切向速度对流体粒子所受离心力有直接影响,轴向速度与流体粒子的停留时间呈正比,径向速度引发流场的偏摆现象,旋涡形状则关系到气泡的捕获位置。
3.1 流场特征分析
选取工况3进行流场特征分析,图3给出了水力旋流器内瞬时速度分布云图,物理时间取15.22 s。
由图3(a)可见,轴向瞬时速度沿轴向剧烈变化,流场分布不连续,且具有非对称性,其中轴向零速包络面为黑色与灰色区域交界面,该面呈蛇形分布;由图3(b)可看出,径向速度在轴向伴有
正负交替,说明流动是不稳定的,这是造成工程中气柱左右摇摆的原因;由图3(c)可见,涡核中心(即切向速度零值点)并非沿中心轴线对称,而是在轴线附近摆动。流场分析表明,LBM能够模拟水力旋流器内的旋流运动,且捕捉到了二次回流现象和涡核的非稳态特征,流场符合水力旋流器典型的分布特点。

图3 工况3瞬时速度分布云图Fig.3 contours of instantaneous velocity in case 3
3.2 平均切向速度分布对比
图4~7为工况1~4时不同截面的平均切向速度分布。由图4可见,本文获得的平均切向速度分布符合兰金涡(Rankine vortex)运动规律,即自由涡和强制涡组成的复合涡运动。中心区域平均切向速度呈线性变化,两端靠近壁面区域平均切向速度逐渐减小;由于壁面作用以及流动耗散的影响,在壁面附近出现较大的速度梯度,且随截面位置下移,切向速度变小。结果对比表明,本文模拟结果与文献[7]的实验结果及模拟结果基本相符。图4中还可以看出,旋转中心位置(即切向速度零点)不在轴线上,且不同截面旋转中心的位置发生偏移,这一现象与文献[3]结论吻合。
通过对比图5和图6可以看出,当Re数相近而粘度变化时,模拟结果与实验结果吻合度相差不大,说明在小范围变化时,粘度对本文采用方法的准确性影响较小。
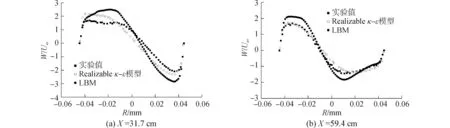
图4 工况1平均切向速度分布Fig.4 Average tangential velocity profiles in case 1
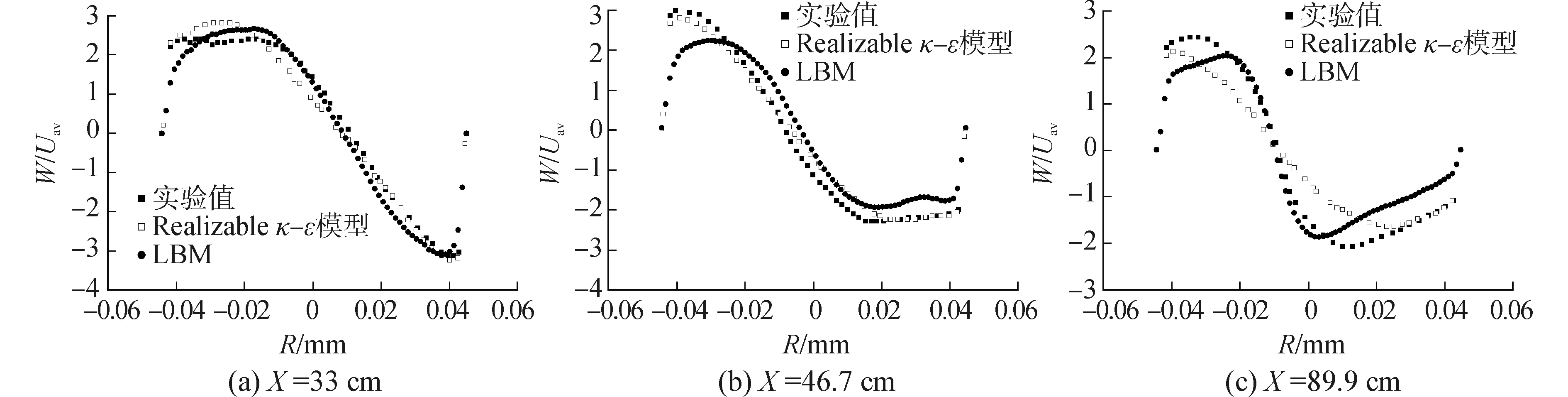
图5 工况2平均切向速度分布Fig.5 Average tangential velocity profiles in case 2
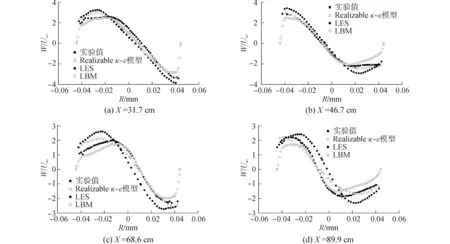
图6 工况3平均切向速度分布Fig.6 Average tangential velocity profiles in case 3
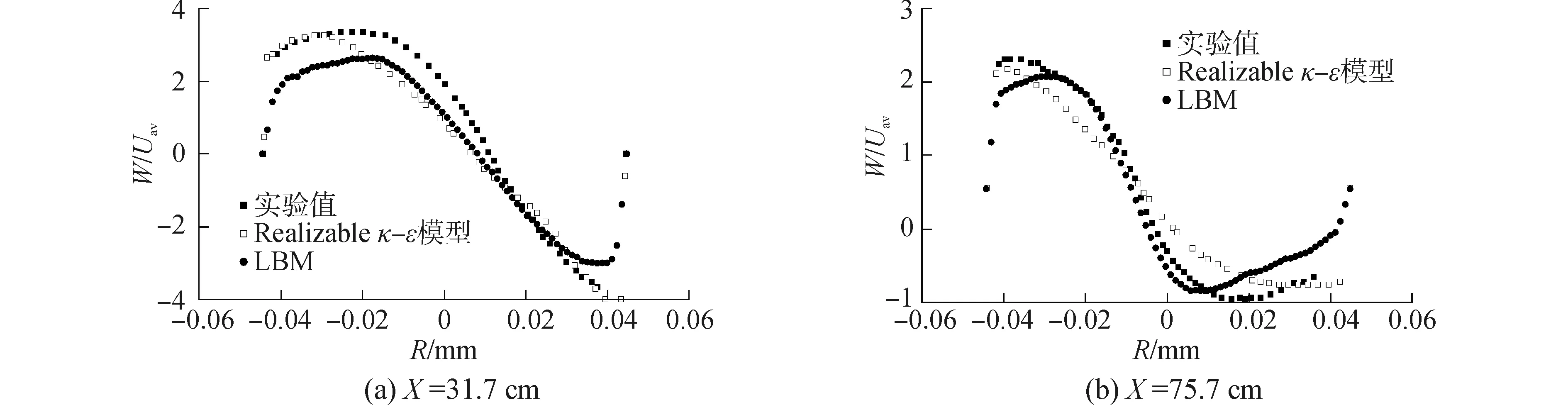
图7 工况4平均切向速度分布Fig.7 Average tangential velocity profiles in case 4
在水力旋流器中,平均切向速度最大值在一定程度上反映了流场的旋流特点,通过式(7)可得到平均切向速度最大值处实验值与模拟值的相对误差:
(7)
式中:WEX为最大切向速度实验值,WLBM为同一位置的模拟值。表2给出了不同工况切向速度最大值的相对误差,其中a、b分别表示本文模拟结果和文献[7]Realizableκ-ε模型的模拟结果。
由表2可见,当Re较小时,本文模拟结果与实验值的相对误差均大于文献[7]模拟结果的相对误差;随着Re增大,两种模拟结果的相对误差值逐渐接近,在部分截面,本文结果与实验值的吻合度高于文献[7]结果;同时,随着Re增大,本文模拟结果与实验结果偏差减小,说明LBM更适用于模拟较大
Re的旋流场。
表2切向速度最大值相对误差
Table2Relativeerrorofmaximumtangentialvelocity

%
由图4~7对比可知:本文模拟得到的各截面平均切向速度分布与实验结果趋势一致,说明LBM能够定性的模拟水力旋流器中存在的旋流运动;与文献[7]相比,本文模拟结果与中心强制旋流区域的实验值更接近,体现了LBM作为介观方法能够真实反映流体粒子间相互作用的特点。与实验结果相比,本文对较小Re旋流场的模拟结果存在偏差,当Re增大后误差减小,说明本文采用方法对较小Re的流场模拟存在局限性;当粘度在小范围变化时,对本文模拟结果准确性影响很小。
对于靠近壁面的平均切向速度,本文模拟结果与实验结果存在一定差异,且大部分速度值小于实验值,分析可能因为本文采用的湍流模型为标准Smagorinsky模型,该模型具有各向同性的特点,且在实际应用中存在耗散过大的问题[14],因而在边界处出现模拟结果与实验结果差异明显的现象;而文献[7]采用的LES模型为WALE模型(即壁面适应局部涡粘模型),WALE模型考虑了旋转张量的影响,在靠近壁面处能获得较好的涡粘性,从而改善了标准Smagorinsky模型湍流耗散量大的问题[15],所以文献[7]的LES模拟结果与实验值更接近。
3.3 平均轴向速度分布对比
图8~11为工况1~4不同截面平均轴向速度分布。由图8可见,本文获得的平均轴向速度分布体现了水力旋流器中沿器壁向下的外旋流运动以及中心轴线附近向上的内旋流运动。结果对比表明,本文模拟结果与文献[7]的实验结果及模拟结果趋势相同。对于靠近壁面的平均轴向速度,与前述切向速度对比结果类似,本文模拟结果与实验结果存在一定差异。
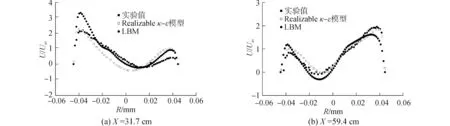
图8 工况1平均轴向速度分布Fig.8 Average axial velocity profiles in case 1
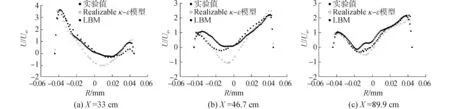
图9 工况2平均轴向速度分布Fig.9 Average axial velocity profiles in case 2
对比图9和图10可看出粘度对平均轴向速度模拟效果的影响。通过对比可见,粘度变化时模拟结果与实验结果吻合度相差不大,说明在小范围变化时,粘度对本文采用方法的准确性影响较小,与上文结论一致。
与切向速度误差处理类似,表3给出了不同工况轴向速度最大值的相对误差。
由表3可以看出,本文平均轴向速度的模拟结果与实验结果存在一定偏差,随着Re增大,误差减小;当Re为66 855时,误差值有所增大,但仍小于工况1的误差;变化趋势与上文切向速度误差对比基本相同。
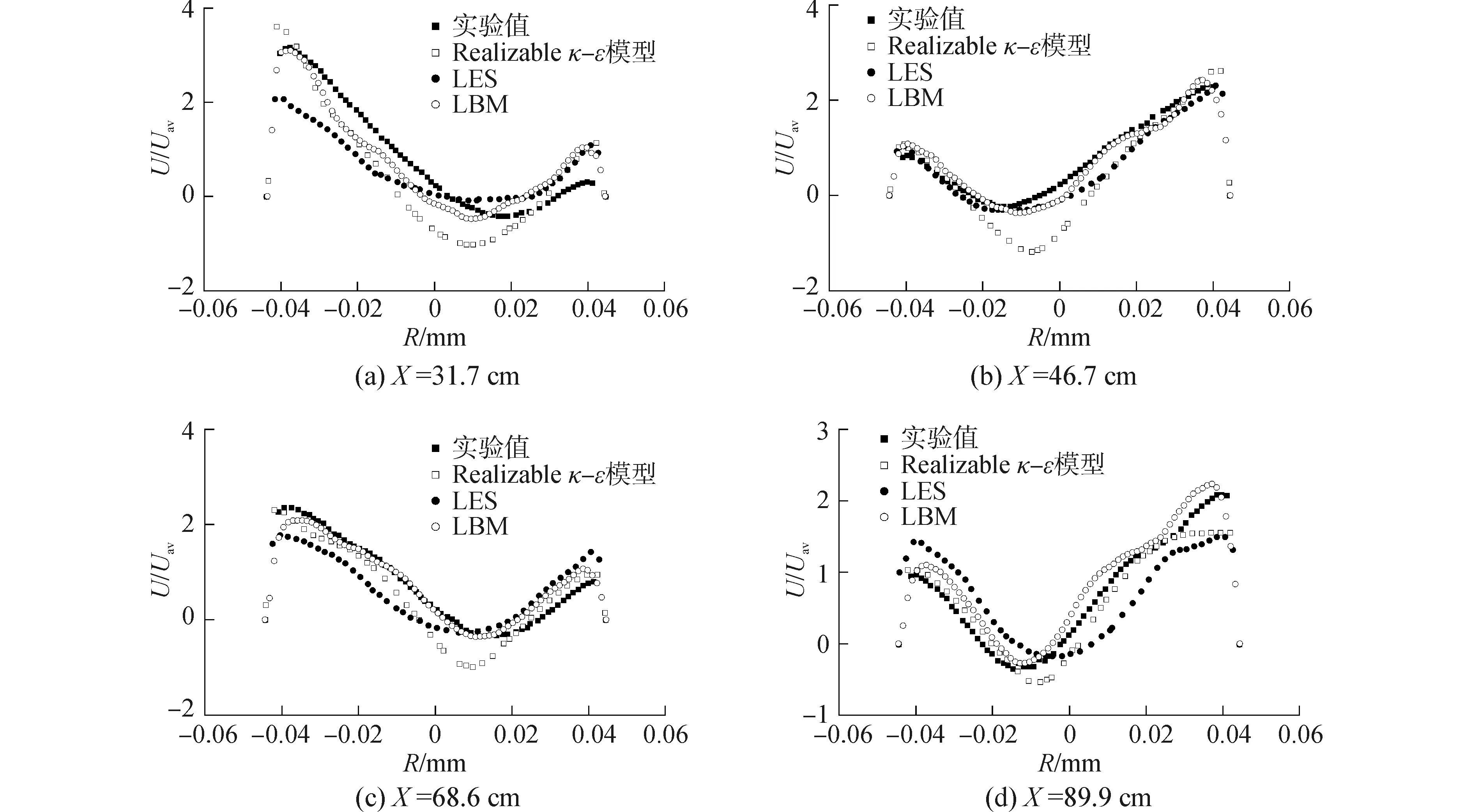
图10 工况3平均轴向速度分布Fig.10 Average axial velocity profiles in case 3
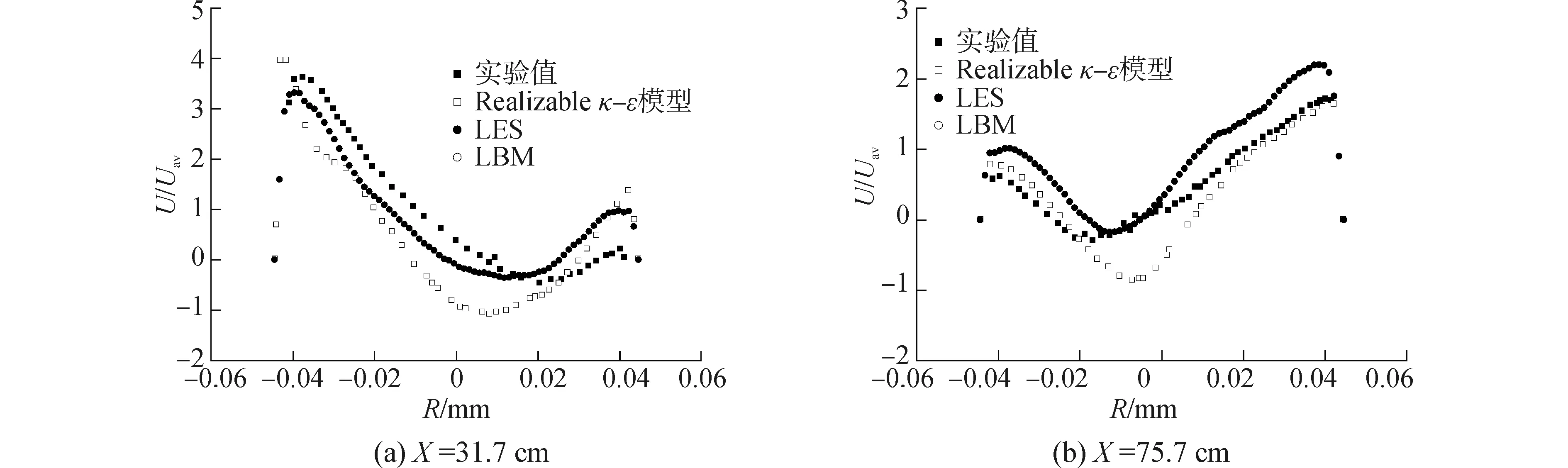
图11 工况4平均轴向速度分布Fig.11 Average axial velocity profiles in case 4
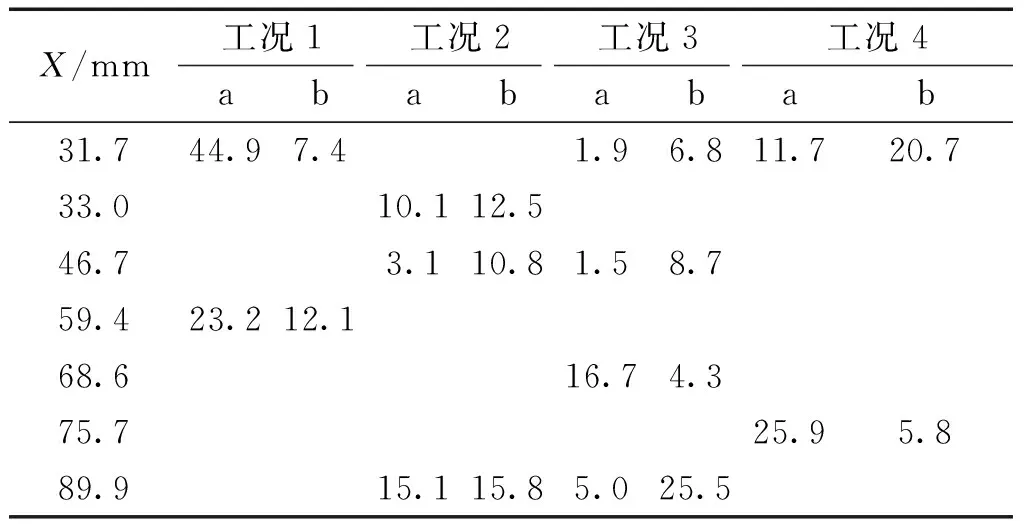
X/mm工况1工况2工况3工况4abababab31.744.97.41.96.811.720.733.010.112.546.73.110.81.58.759.423.212.168.616.74.375.725.95.889.915.115.85.025.5
由图8~11对比可知:本文模拟得到的各截面平均轴向速度分布与实验结果基本吻合,说明LBM能够模拟水力旋流器中存在的二次回流运动;与文献[7]的数值模拟结果相比,本文在水力旋流器中心二次回流区域的模拟结果比实验结果更接近,体现了LBM作为介观方法能够真实反映流体粒子间相互作用的特点。与实验结果相比,本文模拟得到的平均轴向速度分布波动偏大,分析是因为LBM从介观角度出发,更加强调对流体粒子间相互作用的描述,模拟得到的湍流脉动强度大于实验结果,从而造成平均轴向速度分布的波动大于实验结果,这与文献[9]的结论一致。
3.4 平均径向速度分布
在水力旋流器内径向速度测量比较困难,文献[12]也未给出实验结果。针对工况3的平均径向速度分布,图12给出了本文以及文献[7]模拟的结果。
图12(a)中平均径向速度的绝对值随半径减小而增大,这与文献[16]对平均径向速度分布的描述吻合;对比图6和图10可见,径向速度与轴向速度以及切向速度量级相等,这与文献[7]结论相同;同时,由图12(b)可见,沿轴向平均径向速度方向是正负交替变化的,这与文献[7]结果(图12(c))一致。

图12 工况3平均径向速度分布Fig.12 Average radial velocity profiles in case 3
图13为工况3平均轴向速度分布云图,图13中箭头指示方向为根据图12标记的平均径向速度方向,方向的左右交替造成了涡核的偏摆;平均速度与瞬时速度对流场的影响规律一致,但与图3(a)对比可见流场空间形态是不同的,这也体现了涡核位置的瞬时性。
3.5 旋进涡核现象
旋进涡核普遍存在于旋转流动中,是一种非稳态流动现象,它的存在直接影响到水力旋流器的分离过程。为了更清楚的了解涡核的非稳态变化,针对工况3,在模拟过程中每隔0.3 s记录X=89.9 cm截面处涡核中心的位置,涡核中心的运动轨迹如图14所示。
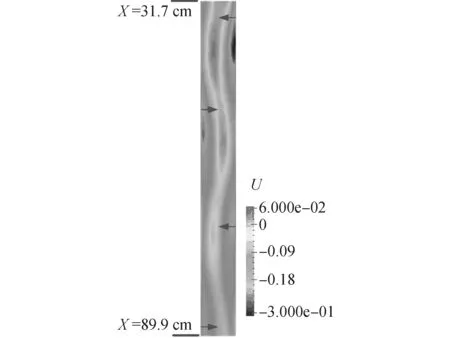
图13 平均径向速度对旋涡的影响Fig.13 Influence of the average radial velocity to vortex
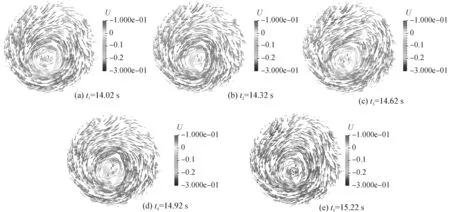
图14 水力旋流器PVC现象Fig.14 PVC phenomenon in hydrocyclone
从图14可以看出,流场存在明显的外旋流和内旋流,其中外旋流方向向下,内旋流方向向上;同时,流场并不是绕着几何中心旋转,呈现明显的非稳态特征。随着时间变化,内外流动区域相对固定,但涡核中心的位置持续变化,且旋转方向与流场旋转方向相反,这与文献[7]结论一致。从上述分析可知,LBM能够定性的模拟水力旋流器存在的旋进涡核现象,且涡核的运动趋势与文献[7]吻合。
4 结论
1)LBM能够模拟出水力旋流器中存在的旋流运动,可捕捉到二次回流现象和涡核的非稳态特征,模拟结果符合水力旋流器典型的分布特点;
2)LBM模拟获得的平均轴向速度和平均切向速度分布与实验结果基本吻合,对流场中心二次流区域的模拟结果比文献[7]更接近实验值,体现了LBM对复杂流动模拟的优势;
3)模拟可得出平均径向速度沿轴向的正负交替变化及流场的旋进涡核现象。
[1] 林基恕, 常春江, 杨九高. 航空发动机设计手册[M]. 北京: 航空工业出版社, 2002.
LIN Jishu, CHANG Chunjiang, YANG Jiugao. Aero engine design manual[M]. Beijing: Navigate Industrical Press, 2002.
[2] GRUSELLE F, STEIMES J, HENDRICK P. Study of a two-phase flow pump and separator system[J]. Journal of engineering for gas turbines and power, 2011, 133(6): 062401.
[3] ERDAL F M, SHIRAZI S A. Local velocity measurements and computational fluid dynamics (CFD) simulations of swirling flow in a cylindrical cyclone separator[J]. Journal of energy resources technology, 2004, 126(4): 326-333.
[4] HREIZ R, LAIN R, WU J, et al. On the effect of the nozzle design on the performances of gas-liquid cylindrical cyclone separators[J]. International journal of multiphase flow, 2014, 58: 15-26.
[5] HREIZ R, GENTRIC C, MIDOUX N, et al. Hydrodynamics and velocity measurements in gas-liquid swirling flows in cylindrical cyclones[J]. Chemical engineering research and design, 2014, 92(11): 2231-2246.
[6] YANG J, ZHANG X, SHEN G, et al. Modeling the mean residence time of liquid phase in the gas-liquid cyclone[J]. Industrial & engineering chemistry research, 2015, 54(43): 10885-10892.
[7] HREIZ R, GENTRIC C, MIDOUX N. Numerical investigation of swirling flow in cylindrical cyclones[J]. Chemical engineering research and design, 2011, 89(12): 2521-2539.
[8] YU H, GIRIMAJI S S, LUO L-S. DNS and LES of decaying isotropic turbulence with and without frame rotation using lattice Boltzmann method[J]. Journal of computational physics, 2005, 209(2): 599-616.
[9] DERKSEN J, VAN DEN AKKER H. Simulation of vortex core precession in a reverse-flow cyclone[J]. AIChE journal, 2000, 46(7): 1317-1331.
[10] LI Y, SHOCK R, ZHANG R, et al. Simulation of turbulent flow in a cyclonic separator with Lattice Boltzmann method[C]//36th AIAA Fluid Dynamics Conference and Exhibit. San Francisco, USA, 2006.
[11] PIRKER S, GONIVA C, KLOSS C, et al. Application of a hybrid Lattice Boltzmann-finite volume turbulence model to cyclone short-cut flow[J]. Powder technology, 2013, 235: 572-580.
[12] ERDAL F M. Local measurements and computational fluid dynamics simulations in a gas-liquid cylindrical cyclone separator[D]. Tulsa: The University of Tulsa, 2001.
[13] BHAMJEE M, CONNELL S H, NEL A L. An investigation into the applicability of the Lattice Boltzmann method to modelling of the flow in a hydrocyclone[C]//South African Conference on Computational and Applied Mechanics. [S.l.],2014.
[14] BEAUBERT F, VIAZZO S. Large eddy simulations of plane turbulent impinging jets at moderate Reynolds numbers[J]. International journal of heat and fluid flow, 2003, 24(4): 512-519.
[15] NICOUD F, DUCROS F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor[J]. Flow, turbulence and combustion, 1999, 62(3): 183-200.
[16] 庞学诗. 水力旋流器技术与应用[M]. 北京:中国石化出版社, 2010.
PANG Xueshi. Technology and application of hydrocyclone[M]. Beijing: China Petrochemical Press, 2010.
本文引用格式:
胡亮, 朱卫兵, 张小彬. 水力旋流器旋流运动的格子Boltzmann模拟[J]. 哈尔滨工程大学学报, 2017, 38(12): 1864-1871.
HU Liang, ZHU Weibing, ZHANG Xiaobin. Lattice Boltzmann simulation of swirling flow in hydrocyclone[J]. Journal of Harbin Engineering University, 2017, 38(12): 1864-1871.
