桨后舵片空化的面元法数值计算方法

叶金铭， 于安斌， 王威， 王友乾

(海军工程大学 舰船工程系，湖北 武汉 430033)

近年来由于舰船向着高速化和大型化方向发展，特别是对于高速舰船，处于螺旋桨后工作的舵的振动和空化剥蚀也越来越严重，因此对舵性能的考虑也越来越全面。20世纪90年代美国海军为了测试桨和舵的水动力性能和噪声特性，进行了一项实船空泡观测试验[1-2]，结果表明，即便是中等海况条件下保持航向航行，23 kn航速时舵表面即出现空泡，舵空泡引起的空化剥蚀在后来的船坞检修中也被证实。舵空泡不仅会使舵效降低，产生空化剥蚀，从而影响舵的水动力性能和使用寿命，更为重要的是，舵空化还会导致船体艉部振动和辐射噪声显著增加，影响舰船的隐身性。

陈建挺等[3]针对某集装箱船的舵空泡在空泡水筒中进行了试验研究，观察了操舵过程中舵空泡产生的情况，探讨了降低舵空化剥蚀的方法。邓鸿等[4]针对大型高速客货船舵系空泡剥蚀现象提出了舵设计阶段应该考虑的关键点。黄昊[5]阐述了在工作过程中遇到的空泡问题，并给出了在实船常规舵系设计中空泡预防的措施。张继静[6]讨论了舵参数对空泡性能的影响。叶金铭等[7-9]采用压力分布和空泡数对比的方法对舵的空化起始航速进行了分析。

Salvatore等[10]采用面元法对三维水翼空泡进行了计算，计算时通过修正的方法考虑了粘性的影响。Koop等[11]用基于欧拉方程的有限体积法对扭曲水翼的空泡进行了计算，并与水洞试验结果进行了比较。Achkinadze等[12-13]采用势流方法对舵的非空化流动和空化流动进行了计算，Vladimir等[14]分别用面元法和RANS方法对桨后舵的片空泡进行了计算，并与试验结果进行了比较，结果证明面元法在计算螺旋桨尾流场、舵的横向力、舵片空泡时与试验结果有较好的一致性。

目前国内对舵空化问题关注得并不多，对舵空化的研究还不够深入，主要是用定性分析的方法来研究舵空化，在舵空化具体数值计算方面还基本上是空白。但随着水面舰船高航速工况使用得越来越频繁，舵空化问题将会越来越突出。本文通过计算螺旋桨的尾流场，采用面元法对桨后舵的片空泡进行数值预报，得到各种航速各种舵角条件下舵表面片空泡的范围和厚度分布，可快速对水面舰船舵空化问题进行定量评估，能为研究舵空化引起的激振力以及进行舵的优化设计提供技术支撑。

1 空泡计算方法

1.1 积分方程

根据Green公式，我们可以通过在物面上布置法向偶极子和源汇以及在尾涡上布置偶极子的方式建立流场中速度势的表达式，从而处理空泡流动问题。布置在舵叶表面表示空泡部分的源汇将使流体边界和固体边界之间存在间隙区域，即空泡区域，对其沿流线方向积分可得到空泡的形状，这一问题和薄翼的厚度问题相似。

对于全湿流动或局部空泡流动，关于扰动速度势的方程为

(1)

式中：P表示控制点，Q表示负荷点。桨叶湿表面上的源强由运动学条件确定，而空泡上的偶极子强度由动力学边界条件确定。因此式(1)成为确定舵叶空泡表面未知源强和湿表面上未知偶强的积分方程。

1.2 动力学边界条件

将Bernoulli方程应用于空泡表面SC，则有

(2)

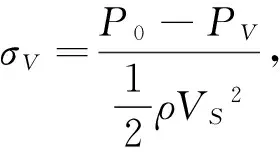
(3)

式中：VS为船速，H为舵的展长。定义Froude数为

(4)

则式(4)变为

(5)

将式(5)应用于空泡分离点和空泡上的任意一点c(为简化，无因次量和原始物理量采用相同符号):

(6)

由式(6)可得：

(7)

(8)

经过对积分表面进行面元划分后，积分方程相应地离散为以面元上的源强和偶强为未知数的方程组。由于事先不知道空泡的范围和形状，这就面临着展向和弦向两个方向上空泡的范围都未知的、空泡的厚度也未知的困难，因此求解空泡问题是比较复杂的。解决的方法之一就是将三维问题分解为两个方向的迭代过程：每一弦向条带上的迭代(第一层迭代)以及弦向条带之间的展向迭代(第二层迭代)，把求解只限于在每一条带上进行，在求解某一条带时，其他条带的源和偶极子强度分布是已知的，这一弦向条带上的源强和偶强求解出来之后，将更新之前的结果，然后把求解的对象转移到下一弦向条带，直到所有弦向条带上的解满足收敛要求。

1.3 计算方法验证

为了验证该方法的计算精度，用该方法对三维水翼的空泡进行了计算。三维水翼剖面为NACA0016翼型的矩形机翼，厚度和弦长之比为6%,展弦比为2.0，攻角为6°，空泡数σV=0.822 ，试验观测结果与计算结果的比较情况见图1。可以看出，对于三维水翼空泡，计算结果和试验观测结果有较好的一致性。

图1 水翼空泡试验观测结果与计算结果比较Fig.1 Comparison of cavitation on hydrofoil between calculation and test results

2 舵片空泡计算

2.1 螺旋桨尾流计算

将螺旋桨的桨叶、桨毂及其尾涡面用四边形双曲面元离散。每个桨叶表面离散为2×M×N个面元，其中M为径向面元数，N为弦向面元数，桨叶的径向方向采用均匀划分，弦向方向采用余弦划分。螺旋桨尾流场可以通过对积分方程式(1)进行梯度求解来实现，得到螺旋桨尾流场中任一点P的扰动速度φ：

φ

(9)

特别地，离尾涡面上比较近的地方，上面的解析公式会产生不合理的结果，这时可以将偶极子的诱导速度转换为走向沿着双曲四边形面元边界的涡环的诱导速度：

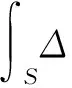
(10)

根据Kerwin提出的计算方法可以得到涡环对近场处的诱导速度。

为了验证该方法对螺旋桨尾流场的计算精度，首先对DTMB4119桨在x/R=0.295,r/R=0.7处的尾流场分别用CFD方法和面元进行了计算，面元法计算时桨叶表面划分的面元数为2×20×20，并和公开发表的实验数据[15]进行了比较，比较结果如图2所示。从比较结果可以看出：除了在螺旋桨尾涡面附近很小的区域内面元法计算结果以及CFD计算结果与实验测量结果有一定的差别外，其他区域上的流场吻合较好；在螺旋桨尾涡面附近的差别主要是由于尾涡面附近的流场具有一定奇异性，用面元法计算会有一定的误差，但该误差主要集中在尾涡面附近很小的区域内，对螺旋桨尾流场的宏观分布影响不大，因此用面元法计算螺旋桨的尾流场作为舵来流输入数据是完全可行的。

图2 DTRC4 119尾流场计算结果与试验测量比较Fig.2 Comparison of DTRC4119 wake between calculation and test results

用上面的尾流计算方法对某水面船30 kn时螺旋桨的尾流场进行计算，并对螺旋桨尾流场进行周向平均处理，计算得到的在舵轴盘面处各半径的速度分布结果如图3，通过插值方法得到舵在不同展长位置的来流速度大小和方向。

2.2 舵片空泡计算结果及分析

将计算得到的螺旋桨尾流场作为计算舵空泡的来流速度场，再用上面建立的舵空泡的计算方法对各航速下不同舵角时的舵空泡形状进行计算。计算舵空泡时，忽略来流的速度脉动，即对计算得到的螺旋桨尾流场进行周向平均处理，计算时考虑舵的侵深，但不考虑打一定舵角时船舶运动漂角对舵进流的影响。舵表面面元数为2×15×20，在18、21、24、27、30、31.5 kn等工况的计算结果见图4所示。

从图4可以看出，相同舵角下，航速越高，舵上的空化范围越大；航速不变时，舵角越大，空泡范围越大；舵角越大，舵的发生空化的起始航速越低。

0°舵角时，舰船在27 kn航速下就会产生空泡，这和文献[8]的分析是一致的。由于该船的吃水较深，舵的浸深较大，舵最易发生空化的展向位置的浸深大于4 m，而一般的水面中高速舰船的吃水比该船明显小，因此这些舰船的舵表面更容易发生空化，0°舵角时舵的空化起始航速会更低。

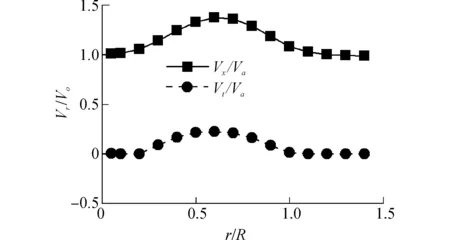
图3 螺旋桨尾流计算结果Fig.3 Calculation results of propeller wake

在5°舵角时，24 kn航速下舵已产生较大范围的空泡。由于舰船航行过程中，通过自动舵保持航向航行是最常用的航行状态，在中低海况条件下，舵角一般会在-5°～+5°内频繁变化，所以该舰船即使以24 kn航速保持航向时，该舵表面也会发生空化。对于采用常规舵的许多中高航速水面舰船而言，由于舵的浸深比该船小，保持航行时舵的空化起始航速一般比24 kn还要小，而其设计航速一般又明显大于24 kn，因此在较大的航速范围内舵会产生较严重的空泡现象。在中高海况时，舰船直航时，自动舵舵角变化范围更大，舵的空化问题也更严重。

舵空化不仅会引起舵面剥蚀，还会导致船体尾部振动和噪声显著增加，因此有必要对舵的设计方法开展研究，设计中应根据螺旋桨尾流场的特点进行舵的匹配设计，以提高舵的抗空化性能，从而避免舵空化带来的不利影响。

图4 舵片空泡计算结果Fig.4 Calculation results of sheet cavitation on rudder

4 结论

1)航速越高，舵角越大，空化问题越严重，对于采用常规舵的一般中高速水面舰船而言，即使是保持航向航行，在较大的航速范围内舵表面也会发生空化，从而引起空化剥蚀、舵效降低、艉部振动和辐射噪声增加等一系列问题。

2)为了避免舵空化带来的一系列问题，根据螺旋桨尾流场的特点进行舵的优化设计，提高舵的抗空化性能。

本文建立的方法可以对水面舰船的舵空化问题进行定量评估，为计算舵空化引起的激振力提供数据输入，也可为开展舵的抗空化设计提供技术支撑。

[1] SHEN Y T, REMMERS K D, JIANG C W. Effects of ship hull and Propeller on rudder cavtation[J]. Journal of ship research, 1997, 4l (3): 172-180.

[2] SHEN Y T, JIANG C W, REMMERS K D. A twisted rudder for reduced cavitation[J]. Journal of ship research, 1997, 41(4):260-272.

[3] 陈建挺，虞贲，胡平. 4250 TEU集装箱船舵空泡试验研究[J]. 上海船舶运输科学研究所学报， 2008， 31(2)： 81-83.

CHEN Jianting, YU Lai, HU Ping. An experimental study of rudder cavitation for 4250 TEU container vessel[J]. 2008, 12(2): 81-83.

[4] 邓鸿，赵成璧. 大型高速客货船的舵空泡剥蚀及解决方案探索[J]. 船舶设计通讯， 2005， 111(1)： 65-69.

DENG Hong, ZHAO Chengbi. Rudder cavitation and solution search for large fast passenger ferry[J]. Journal of ship designs, 2005, 111(1): 65-69.

[5] 黄昊. 民用船舶常规舵系设计的比较及分析[D]. 上海：上海交通大学， 2012： 43-63.

HUANG Hao. Comparison and analysis of conwentional rudder design for civil ship[D]: Shanghai: Shanghai Jiao Tong University, 2012: 43-63.

[6] 张继静. 高速船舵优化及操纵性研究[D]. 哈尔滨：哈尔滨工程大学， 2009： 45-48.

ZHANG Jijing. Study on optimization and maneuverability of rudder on high-speed-ship[D]. Harbin: Harbin Engineering University, 2009: 45-48.

[7] 叶金铭，王威，李渊， 等. 抗空化扭曲舵设计及力学特性研究[C]//2015全国船舶水动力学会议论文集.哈尔滨， 中国，2015： 328-335.

YE Jinming, WANG Wei, LI Yuan, et al. Research on Hydrodynamic performance of anti-cavitation twisted rudder[C]//2015 Symposium on ship hydrodynamics. Harbin, China, 2015: 328-335.

[8] 叶金铭，王威，张凯奇，等. 扭曲舵空化起始航速分析[J]. 哈尔滨工程大学学报， 2016， 37(12)： 1631-1637.

YE Jinming, WANG Wei, ZHANG Kaiqi, et al. Analysis on the cavitation inception speed of twisted rudder[J]. Journal of Harbin Engineering University, 2016, 37(12): 1631-1637.

[9] 叶金铭，王威，于安斌, 等. 抗空化扭曲舵的设计及其水动力性能分析[J]. 上海交通大学学报， 2017， 51(3)： 314-319.

YE Jinming, WANG Wei, YU Anbin, et al. Design and numerical analysis of hydrodynamic performance for anti-Cavitation twisted rudder[J]. Journal of Shanghai Jiao Tong University, 2017, 51(3): 314-319.

[10] SALVATORE F, ESPOSITO P G. An improved boundary element analysis cavitating three-dimensional hydrofoils[C]//Fourth International Symposium on Cavitation. Wageningen, USA, 2001.

[11] KOOP A H, HOEIJMAKERS H W, SCHNERR G H, et al. Design of twisted cavitation hydrofoil using a barotropic flow method[C]//Six International Symposium on Cavitation. Wageningen, The Netherlands, 2006.

[12] ACHKINADZE A S, BERG A, KRASILNIKOV V I, et al. Numerical prediction of cavitation on propeller blades and rudder using the velocity based source panel method with modified trailing edge[C]//International Summer Scientific School “High Speed Hydrodynamics”. Cheboksary, Russia, 2002.

[13] ACHKINADZE A S, BERG A, KRASILNIKOV V I, et al. Numerical analysis of podded and steering systems using a velocity based source boundary element method with modified trailing edge[C]//The Propellers/Shafting’2003 Symposium. Virginia Beach, USA, 2003.

[14] VLADIMIR I K, AAGE B, IVAR J. Numerical prediction of sheet cavitation on rudder and podded propellers using potential and viscous flow solutions[C]//Fith International Symposium on Cavitation. Osaka, Japan, 2003.

本文引用格式：

叶金铭， 于安斌， 王威， 等. 桨后舵片空化的面元法数值计算方法[J]. 哈尔滨工程大学学报， 2017， 38(12): 1844-1848.

YE Jinming, YU Anbin, WANG Wei, et al. Numerical investigation of sheet cavitation of rudder behind propeller by surface-panel method[J]. Journal of Harbin Engineering University， 2017， 38(12): 1844-1848.