工程车辆多电机驱动系统同步协调控制策略
2018-01-15涂群章蒋成明傅中明张洪新
黄 皓,涂群章,蒋成明,傅中明,张洪新
0 引言
为适应工程车辆路况复杂、行驶载荷多变、机动性要求高的要求[1],同时满足乘座舒适性,电传动工程车辆的驱动方式正逐步由单电机驱动向多电机驱动方向发展[2],双侧电机独立驱动是如今运用最多的电传动方案(如法国“响尾蛇”地对空导弹车,德国的“黄鼠狼”步兵战车,美国的M113两栖装甲运兵车等[3]),它具有传动效率高、结构简单、系统布置灵活等优点[4],但由于其两侧电机不存在机械连接,在直线行驶过程中,如果两侧电机受到的地面负载不同,会导致前轮两侧的速度不同步,将会产生车辆方向盘不受控制、跑偏、打滑等问题,这将影响车辆行驶的安全性和舒适性[5-6]。
在实际的多电机传动工程车直线行驶工况中,能否实现在多变载荷工况下,多电机速度的同步协调控制,直接关系到车辆的安全性和舒适性,因而多电机系统的同步协调控制问题是该类车辆研发的一个急需解决的关键问题,目前逐渐成为国内外研究热点[7]。为此,本文针对多电机同步协调控制的发展现状,对多电机协同控制策略进行了论述[8-9],重点介绍和分析了:(1)经典控制策略,主要包括并行方式、主从方式、交叉耦合方式[10];(2)现代控制策略,主要包括偏差耦合控制和环形耦合控制[11];(3)智能控制策略,主要包括基于模糊控制器的同步控制和基于神经网络的同步控制[12-13],探讨了多电机同步控制的发展趋势,为多电机传动工程车辆行驶过程中速度协调控制技术研究提供借鉴。
1 经典控制策略
同步协调控制指的是按照工程要求,实现两个或多个传动轴之间的输出值的协调控制。经典同步控制理论是在20世纪80年代由Y.Koren教授[14]和Robert.D.Lorenz教授[15]创立的,控制方式主要有并行方式、主从方式和交叉耦合方式。
1.1 并行控制策略
并行控制系统中,控制系统中所有单元共享一个控制信号,让每个单元都有理想一致的输出结果,从而使控制系统稳定性优良,动态性能好,并行控制结构图如图1所示。

图1 并行控制结构图
并行控制结构简单,运算较快,控制方便,但是它的缺点也很明显,由于每个电机都是独立控制的,当其中一台或者多台电机受到外界干扰时,这些电机转速会发生变化,而其他电机由于是独立控制的,不会受到影响,这就导致了控制系统失去了同步性[16],这在工程车辆路况复杂、行驶载荷多变的情况下,难以达到要求。
1.2 主从控制策略
以双电机主从控制为例,主从控制系统结构图如图2所示。主电机的输出转速作为从电机的转速的输入参考值,从动机的输出由主电机的输出转速控制,使之达到同步协调控制。在这种控制方法下,每个从电机单元都能准确快速的跟踪参考值,实现良好的跟踪性。
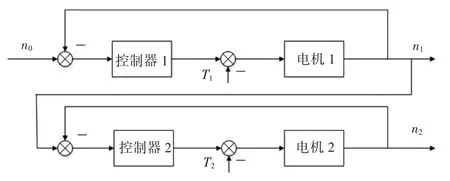
图2 主从控制结构图
从图2可以看出,在主从控制结构下,将一台电机作为主电机,主电机的输出信号为参考信号控制从动机,理想情况下,能达到较好地同步效果,但是假设从动机收到外界负载的干扰,从动机的速度会发生改变,由于主动机不受从动机的控制,主电机的速度不会随之改变,从而导致两电机存在速度的误差,无法达到理想的控制效果。
1.3 交叉耦合控制策略
交叉耦合控制策略是解决多电机同步协调控制十分有效的方法[15],主要运用于解决外界因速的影响对多电机造成的速度不同步问题,针对控制系统中各个对象建立耦合关系,实现系统的同步协调控制,这种控制方式能反映出任何一台电机的负载变化,显著提高了控制精度[6]。交叉耦合控制策略结构图如图3所示。

图3 交叉耦合控制结构图
交叉耦合同步控制策略在实际中已经开始运用,1990年美国俄亥俄州立大学的K.Srinivasan教授运用交叉耦合算法设计出了一种控制器[11],通过系统的运动轨迹斜率实时调整控制器参数,使控制器达到良好的时变性。
2 现代控制策略
随着现代工业的飞速发展,对同步精度的要求越来越高,导致经典控制策略很难满足日益递增的精度要求,更高精度的控制策略需要被创建,导致现代控制策略在经典控制策略的基础上发展出来,主要分为偏差耦合控制策略和环形耦合控制策略。
2.1 偏差耦合控制
针对上述提出的交叉耦合控制策略无法满足三台以上电机的稳定控制,人们研究出了偏差耦合控制,偏差耦合控制主要控制方法是通过比较各个电机的输出速度进行补偿反馈[17]。偏差耦合控制结构图如图4所示。

图4 偏差耦合控制结构图
偏差耦合控制相对于经典控制策略,克服了信号响应延时性大的缺点,同时适用于两台以上的多电机系统,响应迅速,误差较小。西北工业大学[18]以多台无刷直流电机为研究对象,采用偏差耦合控制策略协调系统的同步控制,在Matlab/Simulink中的仿真结果表明了偏差耦合控制策略控制效果优良、无超调现象、响应迅速。
2.2 环形耦合控制
环形耦合控制是利用各个单元之间的速度补偿形成的现代控制策略。环形耦合控制方式同时考虑了被控对象的输出与给定输出之间的误差关系以及相邻单元之间的输出误差关系[19],环形耦合控制策略的结构图如图5所示。

图5 环形耦合控制结构图
大连理工大学[20]在多电机的同步控制领域提出一种基于滑模变结构方法的环形耦合控制策略,经过仿真和实验证明,这种控制方法在控制过程中不受外来干扰和自身参数影响,具有良好的抗干扰性和鲁棒性。
3 智能控制策略
上述的经典控制策略和现代控制策略,在对控制系统设计的过程中必须建立精准的数学模型,但是工业控制中很多复杂的系统,数学模型难以建立,为了解决这类问题,人们将智能控制技术应用于控制器设计中[21],智能控制策略中运用较多的有基于模糊控制器的同步控制和基于神经网络的同步控制。
3.1 基于模糊控制器的同步控制
模糊控制理论以模糊数学为基础,用语言规则表示方法的先进算法技术,将模糊的数学模型利用语言方式表达出来[22-23],其基本结构如图6所示。

图6 模糊控制系统
近年来,模糊技术逐渐运用于多电机同步协调控制,文献[24]设计出了基于模糊控制器的改进耦合多电机同步控制,该控制器结构原理图如图7所示。

图7 基于模糊控制器的改进耦合多电机同步控制系统
在该系统中,各个电机输出速度之间的耦合关系依靠模糊控制器实现,将各个电机的输出转速输入到模糊控制器中,根据制定的模糊规则确定各电机的补偿速度,执行器再将补偿速度反馈到各个电机[25-26],最终达到同步协调控制。
3.2 基于神经网络的同步控制
神经网络控制是20世纪80年代末期发展起来的自动控制领域的前沿学科之一,它是智能控制的一个新的分支。神经网络控制主要由神经网络结构、神经元模型、神经网络学习方法三个内容组成[27-28]。
神经网络神经元模型和生物神经元模型类似,可将其视为多输入单输出的模型[29],其模型如图 8所示。

图8 神经网络神经元结构图
图 8 中,ui表示神经元的内部状态,x1、x2……xn表示输入信号,ωi1、ωi2……ωin表示连接权系数,si表示外部输入信号[30]。神经元模型的数学形式可描叙为:

文献[31]针对两个电机的同步协调控制策略,以控制系统的转速和张力作为输入,提出一种基于神经网络转速和张力的解耦同步协调控制方案,利用RBF网络整定PID控制器参数,这种控制系统具有良好的自适应性和鲁棒性,其控制系统结构图如图9所示。

图9 基于神经网络二电机同步控制图
图中ω0、F0分别为期望电机转速和载荷,ω、F分别为实际运行电机转速和载荷,μ1、μ2为2个自适应PID控制器的输出信号,通过神经元耦合补偿器后的信号μ1、μ2作为两电机变频调速系统的输入信号,采用该神经网络控制方法能够在保证两台电机速度同步的基础上保证载荷F0的恒定,达到了速度和载荷的解耦控制,并且系统具有很好的动态性能[31]。
4 控制策略分析比较
上述控制方法均有优缺点,经典控制策略中并行控制实现简单,操纵容易,但不适合电机受到外界干扰较大的情况。主从控制利用主电机作为控制电机,在理想情况下,可以保持很好的同步效果,但如果从动机收到外界负载的干扰,从动机的速度会随之发生改变,然而主动机不受从动机的控制,主电机的速度不会随之改变,而且主从控制在控制过程中会出现时滞性。交叉耦合控制能够根据要求完成同步反馈控制,极大地提高了同步精度,但不适用于两电机以上的多电机控制。
现代控制策略中偏差耦合控制采用闭环控制,加入偏差耦合控制策略协调各个电机的转速,其不受电机数量的影响,具有同步性能好、响应速度快、超调量小以及鲁棒性强等特点,但是由于结构较复杂,当电机数目较多时,系统的计算量会很大。环形耦合控制是主从控制上发展而来的,系统在启停阶段同步性能较好、响应速度快,但当其中任何一台电机收到速度波动情况下,它就只能通过与之相邻的电机将信号传递给其他电机,一旦数目较多,就会导致控制延时,从而使得系统的计算量较大。
在智能控制策略中,基于模糊控制器的改进耦合多电机同步系统根据各个电机来制定模糊规则,通过模糊推理来整定PID参数,通过仿真和模拟,与传统控制相比具有跟踪迅速、超调量小、单元输出的实际转速误差鲁棒性强等特点。神经网络控制适用于多变量系统的解耦控制,无需测量和辨识被控多变量对象的内部结构和参数,可以得到良好的的解耦效果,但运算量大,控制算法十分复杂,不利于运用到实际工程实践中。
5 发展趋势
多电机同步协调控制具有良好的发展前景,近年来,多电机同步协调控制向着以下几个方面发展与研究。
(1)良好的解耦控制性能。多电机同步控制性能直接受系统参数解耦性能影响,因此在多电机同步控制时要保证强解耦性。
(2)强抗干扰性。在实际运用场合,抗干扰能力是系统控制性能的重要参数,在轮式汽车实际运行的路面会发生各种变化,导致控制参数的漂移,这要求多电机同步协调控制系统具有较强的抗干扰性。
(3)良好的动态响应性。多电机同步控制系统能够根据外界的变化快速达到稳定性,直接影响到多电机同步控制性能,这也是一项重要研究方向。
(4)较高的稳定性。控制系统稳定性是系统能够正常运作的前提,能否提高稳定性,直接关系到系统能否正常运作。提高稳定性也是一项关键技术。
6 结束语
本文对多电机传动工程车辆在直线行驶过程中,多电机同步协调控制的策略进行了研究,论述三种控制策略的原理、特点及实现方法。分析比较了各控制策略的优劣性,对多电机同步协调控制技术的主要问题及其发展进行展望,为电传动工程车辆多电机同步控制系统的研发提供参考。
[1]严 纠.电传动车辆的研究与发展[J].国外坦克,2006(2):44-46.
[2]孙文焕,程善美,王晓翔,等.多电机协调控制的发展[J].电气传动,1999(6):3-6.
[3]孙逢春,张承宁.装甲车辆混合动力电传动技术[M].北京:国防工业出版社,2008.
[4]朱茂林.多电机速度同步控制策略的研究与应用[D].合肥:合肥工业大学,2013.
[5]李 慧,刘星桥,李 景,等.多电机同步协调系统控制策略[J].电机与控制应用,2014(4):6-11.
[6]Chen S,Zhang K,Zhang W,et al.Design of multi-motor synchronous control system[C]//Control Conference,2010:3367-3371.
[7]Li M,Meng X.Analysis and Design of System for Multi-mo tor Synchronous Control[C]//Advances in Computer Science,Environment,Ecoinformatics,and Education-International Conference,Csee 2011,Wuhan,China,August 21-22,2011.Proceedings,2011:268-273.
[8]杨晨娜,张 怡.双电机同步控制系统的设计与仿真[J].工业控制计算机,2009,22(1):36-37.
[9]Zhao W B,Zhu J H,Ji-Heng N I.Research of Multi-Mo tors Synchronous Control[J].Techniques of Automation&Ap plications,2012(4):189-195.
[10]Zhang P,Zhang J H,He D S,et al.Based on Adjacent Cross-Coupling of Multi-Motor Synchronous Drive[J].Ad vanced Materials Research,2011(201-203):1093-1097.
[11]Srinivasan K,Kulkarni P K.Cross-Coupled Control of Bi axial Feed Drive Servomechanisms[J].Journal of Dynamic Systems Measurement&Control,1990,112(2):225-232.
[12]张 莉,李彦明,马培荪,等.基于模糊PID控制器的多电机同步控制装置的应用[J].工业仪表与自动化装置,2003(4):11-13.
[13]Yun-Feng B I,Wang X.Multi-motors'Synchronization Control Based on Fuzzy Control[J].Machinery&Electronics,2008.
[14]Lorenz R D,Schmidt P B.Synchronized motion control for process automation[C]//Industry Applications Society Meet ing,1989.,Conference Record of the,2002(2):1693-1698.
[15]Koren Y.Cross-Coupled Biaxial Computer Controls for Manufacturing Systems[J].Journal of Dynamic Systems Mea surement&Control,1980,102(4):265-272.
[16]刘 艳.多电机同步控制系统控制策略研究[D].沈阳:沈阳工业大学,2013.
[17]彭晓燕,刘 威,张 强.基于改进型偏差耦合结构的多电机同步控制[J].湖南大学学报(自然科学版),2013,40(11):77-83.
[18]喻 鹏,齐 蓉.多无刷直流电动机偏差耦合同步控制[J].微特电机,2008,36(4):42-45.
[19]Sun J,Liu R,Luo Y,et al.Research on Multi-motor Syn chronization Control for Cutter Head of Shield Machine Based on the Ring Coupled Control Strategy[M].Springer Berlin Heidelberg,2009:345-354.
[20]刘 然,孙建忠,罗亚琴,等.基于环形耦合策略的多电机同步控制研究[J].控制与决策,2011,26(6):957-960.
[21]Fan Y.Improvement of multi-motor synchronous control strategy[J].Mechanical&Electrical Engineering Magazine,2007(108):1024-1028.
[22]Passino K M,Yurkovich S.Fuzzy Control[J].Tsinghua U niversity Press,2001,18(4):863-873.
[23]Zadeh L A.Fuzzy Logic[J].Computer,1988,21(4):83-93.
[24]Deng H,Liu H.Multi-motor synchronous control based on fuzzy support vector machine[C]//IEEE International Confer ence on Intelligent Computing and Intelligent Systems,2009:60-63.
[25]Su Y,Gang X.Research of Multi-motor Synchronous Driv ing System Based on Fuzzy Smith Control[C]//International Conference on Electrical and Control Engineering,2010:5466-5469.
[26]ztürk N, elik E.Speed control of permanent magnet syn chronous motors using fuzzy controller based on genetic algo rithms[J].International Journal of Electrical Power&Energy Systems,2012,43(1):889-898.
[27]Simon H.Neural Network:A Comprehensive Foundation[J].Prentice Hall PTR,1994,22(4):71-80.
[28]焦李成.神经网络系统理论[M].西安:西北工业大学出版社,1990.
[29]袁曾任.人工神经元网络及其应用[M].南宁:广西科学技术出版社,1999.
[30]李俊丽,何 勇,王生泽.单神经元PID在多电机同步控制中的应用[J].机电工程,2010,27(8):14-18.
[31]樊卫华,赵国峰,陈庆伟,等.双电机驱动伺服系统神经网络控制器的设计[J].电机与控制学报,2006,10(3):260-264.
