风机叶片多点静力加载试验解耦控制方法研究

2018-01-15乌建中

装备制造技术 2017年11期

乌建中，许旺

风机叶片作为风力发电机组的核心部件之一，对其全尺寸结构检测等领域的研究显得十分重要。根据IEC61400-23标准，对于新研制或者工艺做出重大更改后的叶片，均需做静力加载试验，验证叶片的静强度储备，并为刚度检验以及结构优化设计等提供必要的数据。多点静力加载过程中，各个加载点之间存在交叉耦合情况，导致加载精度不高，需要有效的解耦控制算法以提高加载精度[1]。

本文详细研究了变速积分PID解耦算法与神经网络变速积分PID解耦算法，并对这两种算法进行仿真分析以及现场试验验证；通过对比仿真与试验结果，总结出两种算法的适用范围，据此针对不同的工况选择合适的算法，保证静力加载过程的顺利进行，为深入研究风机叶片的性能打下基础。

1 风机叶片多点静力加载解耦算法分析

1.1 风机叶片多点静力加载耦合分析

风机叶片多点静力加载是多个节点的作用力通过钢丝绳同时作用在叶片上的一种等效加载方式，如图1所示。

图1 多点静力加载装置

根据IEC61400-23标准，各加载点分别按最大载荷40%-60%-80%-100%-80%-60%-40%依次进行逐级加载与卸载，其中在100%阶段载荷持续时间至少10 s，如图2左所示。由于叶片上各节点的夹具位置不同，以及叶片不同截面刚度等特性的差异，产生了不同节点之间载荷耦合情况。如图3所示，风机叶片在力F1作用下A点产生挠度△，当F1、F2、F3同时作用时产生挠度y.即A点的挠度不仅仅与F1相关，F2、F3也对其产生了影响。那么在没有解耦控制算法情况下，多点静力加载将产生非常严重的交联耦合，严重影响叶片试验的正常进行，如图2右所示[2]。

图2 静力加载阶段曲线图

图3 某一节点多点同时加载与单独加载挠度示意图

1.2 离散变速积分PID解耦算法

由于各加载节点存在交联耦合的情况，需要设计一些算法来对整个加载过程进行解耦控制。

传统PID算法在实际载荷与目标载荷误差变化较大时，容易产生积分饱和作用，该作用会引起大幅度的超调，使系统稳定性下降。设法改变积分项的累加速度，使其与偏差大小相对应，即偏差越大，积分越慢，反之越快，以消除积分饱和情况。离散变速积分PID的积分项可表示为：

其中，v（k）为积分环节在采样序列k时输出的控制量。f（e（k+1））与e（k+1）的关系可以是线性的，也可以是非线性的。设

其中，a、b为常量，且a+b＝1；r（k）为时间序列k时设定的输入信号。则

据此离散变速积分PID解耦控制器结构如图4所示，系统输入e（k）为反馈载荷与目标载荷的差值，由公式（3）求得 u（k），经过控制器控制输出，得出反馈载荷。

图4 离散变速积分PID解耦控制器结构

1.3 神经网络变速积分PID解耦算法

不同叶片以及叶片的不同加载方向性能差距较大，为了提高加载系统适应不同叶片刚度变化的能力，采用了BP神经网络与PID相结合的方法，使用BP神经网络在线调整PID的比例系数。据此设计神经网络变速积分PID解耦控制器，如图5所示。各节点输入e（k）为反馈拉力与预设拉力之差，通过变速积分算法得到PID控制器的积分系数ki；同时，偏差e（k），累计偏差 Σe（k）以及偏差增量作△e（k）为 BP神经网络的三个输入，经过神经网络NN得到PID控制器的比例系数kp；由于该系统时滞较短，微分系数设为0.PID控制器输出钢丝绳的绳速，作用在叶片上，得到反馈拉力。BP神经网络变速积分PID解耦控制结构框图如图5所示。

图5 BP神经网络变速积分PID解耦控制结构框图

本文采用3×6×1的神经网络结构，输入层参数 x1，x2，x3分别为偏差 e（k），累计偏差 Σe（k）以及偏差增量△e（k）；输出层的输出为PID控制器的比例系数kp，如图6所示。该算法由前向传播算法和反向传播算法两部分组成，前向传播根据各个神经元中的激活函数以及各个神经元连接权系数计算得出输出结果kp，反向传播根据该结果与预设结果的差值由后层网络向前层网络依次修改神经元连接权系数。其中，隐含层激活函数f（x）=tanh（x）；输出层激活函数 g（x）=0.5（1+tanh（x））。j，i，l分别表示输入层、隐含层、输出层神经元序号。ωij为输入层j号神经元至隐含层i号神经元的连接权系数。ωij为输出层l号神经元至隐含层i号神经元的连接权系数[4]。

图6 BP神经网络结构图

（1）前向传播

1）输入层输入

2）隐含层输出yi（k）

3）输出层输出kp（k）

（2）反向传播

用性能指标函数JS来衡量加载系统性能的优劣。

当系统性能指标函数值大于系统设定值，则系统进行反向传播，调整神经元的连接权系数。例如取设定值为a，当JS>a时按照梯度下降法调整神经元的连接权系数ωij和ωli.

1）隐含层至输出层神经元连接权系数增量为△ω（lik）：

其中：η为学习速率。a△ωli（k-1）是为了加快全局收敛的附加惯性项，a为惯性项系数。

则神经网络输出层至隐含层连接权系数的计算公式为：

2）输入层至隐含层神经元连接权系数增量为△ωij（k）.

同上述方法，隐含层连接权系数的计算公式为：

2 风机叶片多点静力加载解耦算法仿真分析

风机叶片多点静力加载交联耦合可用公式（11）表示：

其中：F矩阵为各节点加载力，矩阵为Y各加载点挠度，T为耦合矩阵。

以风机叶片三点静力加载为例，仿真初始条件如表1，表2所示。

表1 工况一仿真初始条件

表2 工况二仿真初始条件

通过MATLAB建立叶片三点静力加载变速积分PID解耦控制仿真模型，仿真结果如图7、图8所示。可以看出耦合情况变化不大时，变速积分PID解耦控制器可以很好地解耦，如图7所示；当耦合情况发生较大变化时，解耦效果不甚理想，如图8所示。

图7 工况一解耦效果仿真曲线图

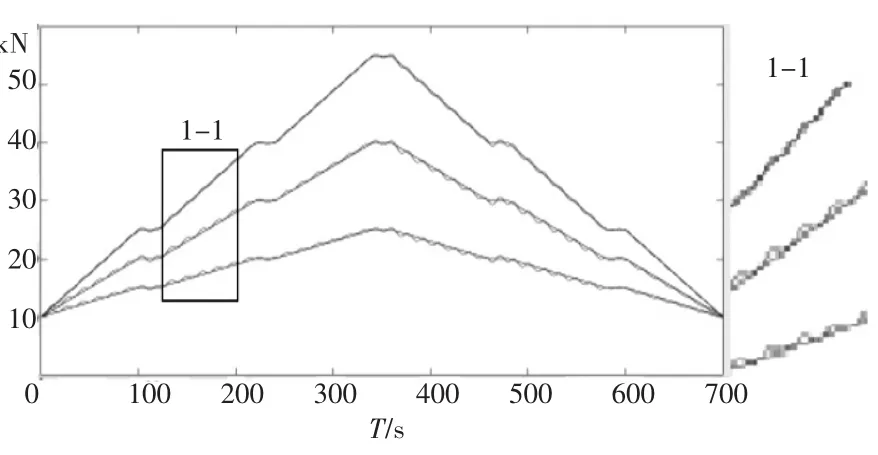
图8 工况二解耦效果仿真曲线图

建立叶片三点静力加载BP神经网络变速积分PID解耦控制仿真模型，仿真结果如图9、图10所示。可以看出对于耦合情况变化不大时，BP神经网络变速积分PID解耦控制器可以很好的解耦，如图9所示；当耦合情况发生较大变化时，仍可获得较好的解耦效果，如图10所示。

图9 工况一解耦效果仿真曲线图

图10 工况二解耦效果仿真曲线图

3 风机叶片多点静力加载试验与分析

基于本文提出的BP神经网络变速积分PID解耦控制算法，进行了现场试验，被加载叶片长度为53.8 m，分别进行了叶片挥舞方向及摆振方向4点静力加载，加载结果如图11、图12所示。现场实测试验结果显示，BP神经网络变速积分PID解耦控制算法在刚度变化较大的叶片挥舞方向与摆振方向都取得了良好的解耦效果，进一步试验表明，该算法在叶片不同加载点数、叶片不同加载方向等刚度变化较大的工况下都可以获得较好的解耦效果。