纤维金属层板低速冲击仿真

蔡艳++张斌++李振友

摘要： 采用JohnsonCook模型模拟铝层的力学行为，选用Hashin三维准则对复合材料层内损伤进行判断，采用CamanhoMatthews折减方案进行刚度折减，同时采用粘接元描述复合层板层间失效，采用Abaqus/Explicit结合VUMAT建立玻璃纤维增强铝合金层板冲击有限元模型。结果表明：随着冲击能量的变大，测量点的位移逐渐变大，钢球反弹后的测量点最大塑性变形也逐渐增大；纤维金属层板的玻璃纤维先发生破坏，然后铝合金层出现裂纹；2种层板的抗低速冲击性能基本相同。研究结果可用于玻璃纤维铝合金层板抗冲击性能的对比分析。

关键词： 纤维金属层板； 低速冲击； Hashin三维准则； CamanhoMatthews折减； 粘接元； 损伤力学

中图分类号： V214.5； TB333文献标志码： B

Simulation on low velocity impact of fiber metal laminates

CAI Yan1， ZHANG Bin1， LI Zhenyou2

（1. Nanjing Polytechnic Institute， Nanjing 210048， China；

2. Shanghai Aircraft Manufacturing Co.， Ltd.， Shanghai 200126， China）

Abstract： The mechanical behavior of aluminum layer is simulated by JohnsonCook model. The Hashin 3D criterion is used to judge the innerlayer damage of composite material layer. The CamanhoMatthews reduction scheme is used to reduce the stiffness， and the mortar element is used to describe the interlayer failure of the composite laminates. The finite element model of the impact on the glass fiber reinforced aluminum alloy laminates is established by combining Abaqus/Explicit with VUMAT. The results show： with the increase of the impact energy， the displacement of the measuring point increases gradually， and the maximum plastic deformation of the measuring point increases gradually after the rebound of the steel ball； the glass fiber of fiber metal laminates is destroyed firstly， then the aluminum alloy layer cracks. The low velocity impact resistance of the 2 laminates is almost equal. The study results can be used for the comparative analysis of impact resistance of glass fiber reinforced aluminum laminates.

Key words： fiber metal laminate； low speed impact； Hashin 3D criterion； CamanhoMatthews reduction； mortar element； damage mechanics

收稿日期： 2017[KG*9〗07[KG*9〗22修回日期： 2017[KG*9〗09[KG*9〗06

作者簡介： 蔡艳（1971—），女，江苏盐城人，工程师，研究方向为过程装备与控制工程，（Email）zbcy418@163.com0引言

纤维金属层板由金属和纤维复合材料交替铺设，并在一定温度和压力下固化而成。玻璃纤维增强铝合金（glass fiber reinforced aluminum alloy， GLARE）层板是一种具有代表性的纤维金属层板。[1]GLARE层板具有轻质、高强、高损伤容限、疲劳性能优异等特点。[2]由于GLARE层板在飞机机身轻量化及抗疲劳方面具有优势，引起研究机构的广泛关注，国外已广泛应用于客机制造上。[35]利用复合材料的力学理论，结合纤维金属层板的性能与结构特点，进行该类材料的低速冲击性能预测，既可深入掌握复合材料的失效分析方法，又可减少庞大的试验工程，同时对国产大飞机材料的选择具有指导作用。

1模型建立

1.1铝合金模型

JohnsonCook模型能够描述金属等材料的应变硬化效应、应变率强化效应和温度软化效应[6]，其表达式为σ=（A+Bεn）（1+Cln *）（1-（T*）m）（1） 式中：σ为等效应力；ε为等效塑性应变；*=/0为等效应变率，0为参考应变率；A，B，n，C和m为5个待求的参数。A+Bεn，1+Cln *和1-T*m分别描述材料的应变硬化效应、应变率强化效应和温度软化效应，其中T*=（T-Tr）/（Tm-Tr）（2）式中：Tr为室温；Tm为材料的熔点。endprint

在不考虑材料的温度软化效应的情况下，对应力应变曲线进行拟合只需要得到JohnsonCook模型方程中的A，B，C和n这4个参数。

铝合金的断裂准则基于JohnsonCook失效模型，失效表达式为εu=（D1+D2exp（D3η））（1+D4ln（*））（3）式中：D1，D2，D3和D4为4个失效模型参数。

在单向拉伸试验中η=-1/3，因此，式（3）可以转化为εu=（D1+D2exp（-D3/3））（1+D4ln（*））（4）JohnsonCook失效模型的参数采用文献[7]中的参数，见表1。有限元仿真中具體的材料失效模型参数见表2。直接在Abaqus/CAE中建模，铝合金使用C3D8R体单元。

1.2复合材料层内模型

对于复合材料层内失效，准则均应能在一定程度上反映复合材料的损伤。本文采用Hashin三维损伤准则[8]，具体损伤模式定义如下。

纤维拉伸（σ1>0）时QFFT=σ1XT2+τ212+τ213S212（5）纤维压缩（σ1<0）时QFFC=σ1XC2（6）基体拉伸（σ1+σ2>0）时QMFT=σ2+σ3YT2+τ223-σ2σ3S223+τ212+τ213S212（7）基体压缩（σ1+σ2<0）时QMFC=YC2S232-1σ2+σ3YC+σ2+σ32S232+τ223-σ2σ3S223+τ212+τ213S212（8）式中：QFFT，QFFC，QMFT和QMFC为损伤模式判断指标，当QFFT>1时表示复合材料纤维拉伸断裂，当QFFC>1时表示复合材料纤维挤压断裂，当QMFT>1时表示复合材料基体拉伸断裂，当QMFC>1时表示复合材料基体挤压断裂；XT为1方向的拉伸强度；XC为1方向的压缩强度，YT为2方向的拉伸强度；YC为2方向的压缩强度；S12为1层与2层间的剪切强度；S23为2层与3层间的剪切强度；σ1，σ2和σ3分别为3个方向的正应力；τ12，τ23和τ13分别为3个方向的剪应力。

试验中的纤维金属层板为GLARE材料，纤维层采用S2玻璃纤维，在Abaqus中使用C3D8R单元建模，具体参数见表3。表 3玻璃纤维属性参数

Tab.3Glass fiber property parameters参数参数值参数参数值密度ρ/（kg/m3）1 800拉伸强度XT/MPa1 900弹性模量E11/MPa54 000压缩强度XC/MPa800弹性模量E22/MPa9 400拉伸强度YT/MPa57弹性模量E33/MPa9 400压缩强度YC/MPa285泊松比v120.278拉伸强度ZT/MPa57泊松比v230.4压缩强度ZC/MPa285泊松比v130.278剪切强度S12/MPa75剪切模量G12/MPa5 600剪切强度S23/MPa30剪切模量G23/MPa2 500剪切强度S13/MPa75剪切模量G13/MPa5 600

材料性能的退化主要分为突然退化和渐进退化两种。突然退化是指损伤一出现就使模型中相应的材料性能参数值退化为0或者很小，渐进退化是指材料性能的退化以某些演化变量的函数形式逐渐变化。因此，可通过对相应的应力分量进行一定折减实现有限元单元刚度的退化。本文采用CamanhoMatthews折减方案[9]，具体应力更新方案（即刚度退化方案）见表4，其中1代表材料没有受损，其他参数表示材料的折减率。

表 4CamanhoMatthews刚度退化方案

Tab.4Stiffness degradation schemes of CamanhoMatthews损伤模式E11E22E33G12G23G13纤维拉伸断裂0.0711111纤维挤压断裂0.1411111基体拉伸断裂10.2010.200.201基体挤压断裂10.4010.400.401

复合材料层内失效的有限元模拟采用损伤渐进演化的方法，层内的应力、应变分析利用Abaqus/Explicit模块实现，单元材料本构分析、层内损伤起始判定、层内损伤演化法则的建立均通过自编用户子程序VUMAT实现，其流程见图1。

1.3复合材料层间模型

纤维金属层板的层间失效模型采用Abaqus中自带的粘接元材料模型。该模型可以有效地模拟2个不同相位的材料之间的粘接关系，并且允许法向上的外物作用。主面和从面之间的变形根据从层间的节点位移进行计算，失效判据采用常用的BenzeggaghKenane准则[10]，该模型把层间作用分为法向和切向2个方向，分别记为Mode I和Mode II，并给出2个不同的刚度进行仿真计算。层间失效模型参数见表5。

2仿真过程

冲击有限元模型的冲头参考Instron Dynatup 9250 HV落锤冲击试验机的冲头，冲头形状为半球形，半径8 mm，长度35.5 mm，质量10 kg，冲击速度范围为1.5～2.5 m/s。冲头真实形状见图2。在有限元建模时可以把冲头简化成球体形状的解析刚体，半径为8 mm，将质量设置在参考点上。纤维金属仿真选取GLARE 1#和2#。有限元模型四周固定约束，采用六向固支方式进行约束。具体试件尺寸见表6。在纤维金属层板的低速冲击过程中，假设：（1）冲头本身无明显变形，在有限元分析中可认为冲头是刚体；（2）冲头与冲击靶板的相对位移较小，忽略冲击过程中的摩擦力做功。

2.1相同冲击能量的高、低速冲击对比

在相同冲击能量作用下，对比分析高速冲击和低速冲击的不同。选取1#纤维金属层板作为研究对象，冲头质量设置在参考点上，整个钢球模型设置为解析刚体。高速冲击时钢球的半径为3 mm，质量为1.695 4×10-3 kg；低速冲击时的钢球半径为8 mm，质量为10 kg。具体工况见表7。

在钢球低速和高速冲击作用下，纤维金属层板都未发生穿透现象。2种冲击速度时钢球的能量时间图分别见图4和5。在冲击过程中，钢球能量都先下降到0然后呈上升的趋势，这说明钢球的速度先减少到0然后再增加，钢球都出现反弹现象。endprint

2个工况层板的变形云图分别见图6和7。由此可以发现：在冲击过程中，纤维金属层板的玻璃纤维先发生破坏，然后铝合金层出现裂纹，虽然都没有发生穿透现象，但是两者的失效模式仍有不同。在低速冲击过程中，钢球接触纤维金属层板后，玻璃纤维先发生破坏，随后与之接触的铝合金层开始出现断裂，而背面的铝合金层由于延展性良好，所以断裂不明显，最后纤维金属层板发生回弹。对于高速冲击来说，由于冲击速度很大，冲击过程更多地表现出瞬时性。在高速冲击过程中，玻璃纤维率先发生破坏，随后的铝合金层都出现一定程度的破坏。纤维金属层板受低速和高速冲击的主要区別，是在低速冲击过程中纤维金属层板出现明显的分层现象，而高速冲击的分层现象不明显。

2.2不同低速冲击的冲击响应

选取1#纤维金属层板作为研究对象，钢球半径为8 mm，质量为10 kg，质量设置在参考点上，整个钢球模型设置为解析刚体。具体工况见表8。2组工况对应的层板测量点位移时间图和钢球能量时间图分别见图8和9。在图8中，随着冲击能量逐渐增大，测量点的位移也逐渐变大，同时钢球反弹后的最大塑性变形也越大，这与事实相符。在图9中，钢球能量都下降到0然后又上升，说明钢球的速度先减小到0然后再增大。这说明纤维金属层板都没有出现穿透现象，钢球在纤维金属层板上产生反弹。在图中还可以看到，钢球的冲击能量越大，钢球的反弹速度也越大，这也与事实相吻合。

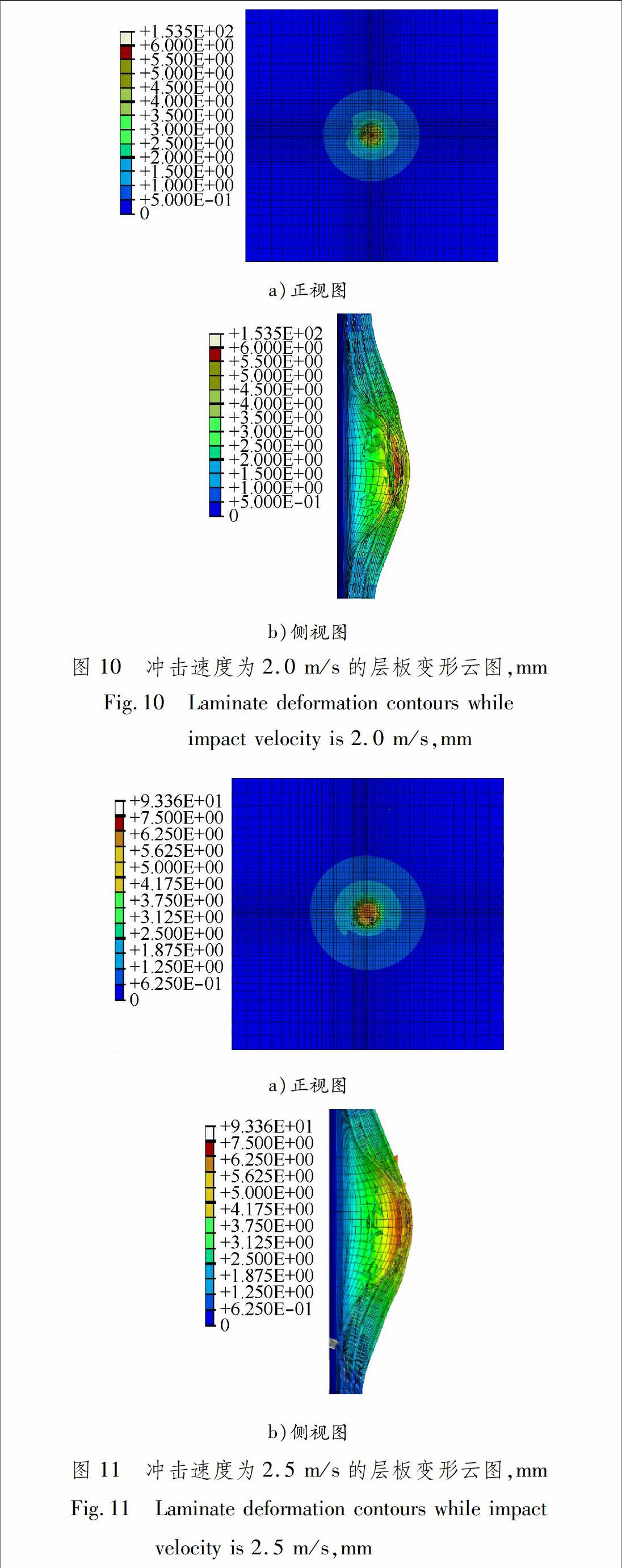
2个工况层板的变形云图分别见图10和11。由此可以发现：在冲击过程中，纤维金属层板的玻璃纤维先发生破坏，然后铝合金层出现裂纹，并没有发生穿透现象；当钢球的冲击速度增大时，纤维金属层板的位移也增大，2个工况都出现分层现象。

2.3不同类型纤维金属层板的冲击响应

仍取钢球的半径为8 mm，质量为10 kg，质量设置在参考点上，整个钢球模型设置为解析刚体，研究不同类型纤维金属层板的冲击响应。取冲击速度为2.0 m/s，冲击能量为20.00 J，2种层板对应的层板测量点位移时间图和钢球能量时间图分别见图12和13。在图12中，2种层板在测量点的位移都先增大再减小。在图13中，钢球的能量都下降到0然后又上升，说明钢球的速度先减小到0然后再增大。这说明纤维金属层板没有出现穿透现象，钢球产生

反弹。在相同的低速冲击载荷作用下，2种纤维金属层板抗低速冲击性能基本相同。

2种层板的变形云图分别见图14和15。由此可以发现：在冲击过程中，纤维金属层板的玻璃纤维先发生破坏，然后铝合金层出现裂纹，没有发生穿透现象；2种层板都出现分层现象。

3结论

基于Instron Dynatup 9250 HV落锤冲击试验，采用Abaqus/Explicit，结合用户自定义子程序VUMAT，模拟冲头冲击纤维金属层板的过程，得到如下结论。

（1）在相同冲击能量作用下，高速冲击和低速冲击的纤维金属层板都未发生穿透现象。低速冲击时铝合金的延展性体现得更强，并且出现分层现象；高速冲击时由于冲击速度很大，冲击过程更多地表现出瞬时性。与低速冲击相比，高速冲击时层板回弹不明显。

（2）在低速冲击过程中，随着冲击能量的增大，测量点的位移也逐渐增大，同时钢球反弹后的最大塑性变形也增大。

（3）在相同的低速冲击能量作用下，2种纤维金属层板的抗冲击性能基本相同。参考文献：

[1]VLOT A， VOGELESANG L B， de VRIES T J. Towards application of fiber metal laminates in large aircraft[J]. Aircraft Engineering and Aerospace Technology， 1999， 71（6）： 558570. DOI： 10.1108/00022669910303711.

[2]WU G C， YANG J M. Mechanical behavior of GLARE laminates for aircraft structures[J]. Journal of Minerals， Metals & Materials Society， 2005， 57（1）： 7279. DOI： 10.1007/s1183700500674.

[3]陶杰， 李华冠， 潘蕾， 等. 纤维金属层板的研究与发展趋势[J]. 南京航空航天大学学报， 2015， 47（5）： 626636. DOI： 10.16356/j.10052615.2015.05.002.

TAO J， LI H G， PAN L， et al. Review on research and development of fiber metal laminates[J]. Journal of Nanjing University of Aeronautics & Astronautics， 2015， 47（5）：626 636. DOI： 10.16356/j.10052615.2015.05.002.

[4]马玉娥， 胡海威， 熊晓枫. 低速冲击下FMLs、铝板和复合材料的损伤对比[J]. 航空学报， 2014， 35（7）： 19021911. DOI： 10.7527/S10006893.2013.0539.

MA Y E， HU H W， XIONG X F. Comparison of damage in FMLs， aluminum and composite panels subjected to lowvelocity impact[J]. Acta Aeronautica et Astronautica Sinica， 2014， 35（7）： 19021911. DOI： 10.7527/S10006893.2013.0539.endprint

[5]陈勇， 庞宝君， 郑伟， 等. 纤维金属层板低速冲击试验和数值仿真[J]. 复合材料学报， 2014， 31（3）： 733740. DOI： 10.13801/j.cnki.fhclxb.2014.03.026.

CHEN Y， PANG B J， ZHENG W， et al. Tests and numerical simulation on low velocity impact performance of fiber metal laminates[J]. Acta Materiae Compositae Sinica， 2014， 31（3）： 733740. DOI： 10.13801/j.cnki.fhclxb.2014.03.026.

[6]JOHNSON G R， COOK W H. Fracture characteristics of three metals subjected to various strains， strains rates， temperatures and pressures[J]. Engineering Fracture Mechanics， 1985， 21（1）： 3148. DOI： 10.1016/00137944（85）900529.

[7]KAY G. Failure modeling of titanium614V and 2024T3 aluminum with JohnsonCook material model： UCRLID149880[R]. US Department of Energy， 2003. DOI： 10.2172/15006359.

[8]HASHIN Z. Failure criteria for unidirectional fiber composites[J]. Journal of Applied Mechanics， 1980， 47（2）： 329334. DOI： 10.1115/1.3153664.

[9]CAMANHO P P， MATTHEWS F L. A progressive damage model for mechanically fastened joints in composite laminates[J]. Journal of Composite Materials， 1999， 33（24）： 22482280. DOI： 10.1177/002199839903302402.

[10]BUI Q V. A modified BenzeggaghKenane fracture criterion for mixedmode delamination[J]. Journal of Composite Materials， 2011， 45（4）： 389413. DOI： 10.1177/0021998310376105.（編辑武晓英）第26卷 第6期2017年12月计 算 机 辅 助 工 程Computer Aided EngineeringVol.26 No.6Dec. 2017endprint