多物理场耦合软件GTEA开发及应用

明平剑++张文平

摘要： 围绕多物理场耦合问题，基于连续介质假设，采用非结构化网格和有限体积方法开发多物理场耦合并行计算软件GTEA。该软件包括计算流体力学、结构应力波传播、流声耦合和声固耦合等4个功能模块。介绍GTEA前处理网格读取、网格格式转换、求解器开发等关键技术。通过柴油机缸内工作过程模拟、船舶水动力计算、自然对流与辐射传热耦合作用、流场动力噪声计算和结构声耦合计算等5个典型应用展示该软件的应用能力和适用范围。

关键词： 多物理场； GTEA； 有限体积方法； 非结构化网格

中图分类号： TP319文献标志码： B

Development and application of multiphysics

field software GTEA

MING Pingjian， ZHANG Wenping

（College of Power and Energy Engineering， Harbin Engineering University， Harbin 150001， China）

Abstract： According to the coupling issue of multiphysics field， based on continuous medium hypothesis， a multiphysics field coupling computing software GTEA is designed using the unstructured mesh and the finite volume method. The GTEA software consists of 4 functional modules， which are computational fluid dynamics， structural stress wave propagation， fluidacoustic coupling， and acousticstructure coupling. The key techniques are introduced such as the preprocessing mesh input， mesh format conversion， and numerical solver development. Five typical applications are selected to show the capabilities and applications of the software， including the simulation of incylinder working process of diesel engine， the calculation of ship hydrodynamics， the coupling effect of natural convection and radiation heat transfer， the dynamic noise calculation of flow field， and structureacoustics coupling simulation.

Key words： multiphysics field； GTEA； finite volume method； unstructured mesh

收稿日期： 2017[KG*9〗09[KG*9〗06修回日期： 2017[KG*9〗09[KG*9〗08

基金項目： 国家自然科学基金（51206031，51479038）；中央高校基本科研业务费重大项目（HEUCFP201711）

作者简介： 明平剑（1980—），教授，博导，研究方向为舰船柴油机性能及多物理场耦合计算方法，（Email）pingjianming@hrbeu.edu.cn0引言

随着制造业数字化时代的到来，软件的重要性日趋显现，软件开发起着举足轻重的作用，计算科学发展成为影响国家利益与国家安全的战略性问题。一些国家将计算机建模与仿真列为优先发展的、服务于国家利益的关键技术。有国内学者指出应将自主CAE软件的开发提高到战略发展的高度。

国内外已有大量的通用和专用CAE软件。2003年，哈尔滨工程大学启动CFD软件开发工程，2007年取得软件著作权，并成功应用于燃烧室内的流动、传热与燃烧过程分析，柴油机缸内工作过程模拟以及船舶水动力学分析等，2008年进行计算声学和结构应力波模拟软件开发，并对结构振动与噪声问题进行数值预报。

1网格前处理与转换技术

对于数值计算的程序开发人员来说，划分求解域网格、得到求解域网格信息（例如网格坐标、网格组成网格面系列等）是一项重复、复杂的工作。有经验的研究人员能够自己写出各种网格信息，但仅限于几何结构简单、网格数量较少的场合；对于非专业进行CFD求解器开发的研究人员，自己写出复杂问题的非结构化网格信息并保证不出错误有一定难度。因此，采用一种折中的方法，团队最初开发CGNS（CFD general notation system）标准格式文件，自编程序读取CGNS格式文件的网格信息并处理输出，应用于自行开发的求解器，可提供标准文件接口。[1]采用通用的网格生成器，如ICEM CFD，可以生成CGNS格式网格文件。为进一步支持主流的CFD软件的前处理格式文件，提高软件的通用性，课题组又先后开发前处理软件GAMBIT生成mesh格式文件，开发STARCCM+软件生成网格文件。

CGNS系统可作为一种标准，将核心求解器研发与商用前处理和后处理软件联系起来。核心求解器开发人员采用CGNS系统作为标准接口，可以解决网格生成和计算结果后处理问题。采用CGNS标准作为输入输出格式，可以读取非结构网格和混合网格，包括二维三角形和四边形网格，三维四面体、六面体和金字塔形网格。endprint

随着网格自适应和直角网格技术的发展，如商用软件STARCCM+和开源软件Openfoam等的广泛应用，对多边形和多面体网格前后处理的需求越来越大，因此，考虑采用非结构化网格有限体积法开发软件，而且基于面循环的方法形成系数矩阵，该方法适用于多边形和多面体网格。针对多边形网格和多面体网格生成器难以转化为CGNS标准格式这一问题，开发直接读取Openfoam网格文件的接口程序，新版tecplot在原有的基于单元的结果输出基础上，新增基于面输出的方法，包括多边形和多面体单元。

2GTEA求解器算法

2.1基本方程

开发多物理场耦合并行计算软件GTEA的前提是连续介质假设，在连续介质力学思想下统一流体力学、固体力学、声波动控制方程，详细过程可以参考文献[2]。该软件分为计算流体力学、结构应力波求解、流声耦合和声固耦合4个功能模块，采用非结构化网格离散控制方程，基本思想见图1。

2.2并行计算流程

GTEA基本流程见图2。GTEA在串行计算程序的基础上进行并行设计。与串行程序相比，并行计算增加区域分解和结果重建2个部分。程序开始运行后读取网格，根据计算环境判断是否存在多个进程，若存在多个进程，则在主进程中根据进程数目划分网格并映射到各进程。读取设置参数后进行离散形成线性方程组，利用并行解法进行计算求解，方程组循环收敛后，通过通信更新变量，准备下一步计算。在计算过程收敛后输出结果，当存在多进程时增加输出子区计算结果，并在主进程中增加调用结果重建环节。在程序线性方程并行计算过程中，各相邻区域之间通过MPI进行通信，线性方程组求解过程需要全局通信。[3]

当存在多进程计算时，需要根据进程数目将网格划分成相应的子区。主进程区域分解调用METIS软件系列的partdmesh工具。METIS软件包含不同的工具，如partnmesh和partdmesh，对于不同的进程数，二者的分区效率不同。为支持任意混合网格，先将网格文件转化成图形文件，然后调用KMETIS划分图形。前者以网格节点为节点转化图形文件，后者则以单元为节点转化。partdmesh可以使各相邻区域间通信量最小，而且各进程间负载较平衡。

在区域分解模块中，采用METIS工具根据进程数将计算域分解，采用主从模式，区域分解模块在主程序中调用，区域内的每个单元按所在的进程进行标识，形成子区内部单元与ghost单元。子区域网格的构建依賴于通信模式的选择，因此在介绍子区域网格构造之前先对通信模式进行说明。以交界面和相邻单元为基础，通信模式主要有2种，见图3。图 2GTEA软件计算基本流程

3仿真算例

3.1柴油机缸内工作过程模拟

某柴油机缸内工作过程模拟中的层动区域和滑移边界的应用示意见图4。红线为静止的不匹配网格边界，主要有2个：一个是气道区域与气阀区域的衔接处，一个是燃烧室区域与气缸区域的衔接处。蓝线为滑移边界，主要在气阀内部区域与外部区域的交接处以及气阀外部区域与气缸区域的交界处。区域1为适应阀杆运动的层动区域，区域2为跟随气阀运动的区域，区域3为适应气阀上表面运动的层动区域，区域4为适应气阀底部和活塞运动的层动区域，区域5为适应活塞运动的气缸层动区域。除区域2外，其他区域均为层动区域。计算过程不同时刻的网格和流场分别见图5和6。

3.2船舶水动力计算

船舶水动力计算简化模型[4]示意见图7。计算域大小为3.220 m×1.000 m×1.000 m，障碍物位于矩形水箱底部、水体前侧，大小为0.160 m×0.400 m×0.160 m，距离布置水体侧壁面2.480 m。初始水体大小为1.228 m×1.000 m×0.550 m。在矩形水箱底部H（0.582，0.500）点设置波高仪监测自由液面高度，在障碍物表面P（2.400，0.475，0.100）点设置压力传感器监测压力大小。

计算模型网格取结构化网格，网格数为161×50×50。自由面高度监测点H点自由面高度随时间变化曲线见图8，压力监测点P点的压力随时间变化曲线见图9。计算结果与实验结果吻合良好。a）分解前区域

3.3自然对流与辐射传热耦合作用

自然对流与辐射传热耦合作用模型示意见图10a）。一个边长为L的正方形封闭方腔，腔体左侧和右侧竖直壁面分别为低温和高温壁面，其温度分别为Tc和Th，上、下壁面绝热，重力方向向下。方腔中的介质是有发射性、吸收性和各向同性散射性的漫灰介质，所有壁面均可认为是黑体。空间被分成60×60的不均匀四边形网格，见图10b）。普朗克数Pl=（k/L）/（4σT30）=0.02，普朗特数Pr=cp/k=0.71，壁面发射率ε=1，消光因数β0=1，θ0=T0/（Th-Tc）=1.5，Tc/Th=0.5。详细计算方法与结果分析可参考文献[5]和[6]。

3.4流场动力噪声

流场动力噪声计算模型和网格划分见图12。采用相同的模型和网格在圆柱壁面附近进行加密。圆柱直径d=0.019 m，流场马赫数Ma=0.2，雷诺数Re=200，介质为空气。计算时间步长为dt=2×10-5 s，总计算时间t=0.15 s，当不可压流场计算趋于周期变化时，即当t=0.05 s时开始计算声场。流场计算左边界为速度进口，右边界为压力出口，上下为对称边界，域内正方形为内部面。在声场计算中，域内正方形到外边界为完全匹配层（perfectly matched layer，PML）区域。4个监测点分别设于A（0，10.0d），B（0，35.0d），C（0，44.9d）和D（0，45.1d）。

3.5结构声耦合算例

某大坝水库结构声耦合系统示意见图14。大坝的弹性模量E=3.437×109 Pa，泊松比μ=0.25，密度ρs= 2 000 kg/m3，纵波波速为cp=1 436 m/s。水中的声速ca=1 436 m/s，水的密度ρa=1 000 kg/m3。水面高度H=50 m，均匀分布的正弦载荷F（t）=200×sin 18t N/m作用在大坝顶部。大坝底部采用固支边界条件，水库上侧水面为绝对软边界，下侧固体壁面为绝对硬边界，右侧为吸收边界。在结构子域、声学子域内均采用显式求解。endprint

先采用常应变型四边形单元模型进行计算，然后进行改进，采用双线性四边形单元求解。边界上的网格尺寸[7]为5.000 m，结构子域中网格的最大边长Lmax≈9.038 m，最小边长为Lmin≈2.744 m，声学子域中Lmax=Lmin=5.000 m。基于显显耦合格式求解，依据稳定性条件，结构子域的时间步长需满足Δts≤1.91×10-3 s，声学子域的时间步长要满足Δta≤3.48×10-3 s，最终结构子域与声学子域取相同时间步长为1.5×10-3 s。

计算A点位移uy和B点声压p随时间的变化，并将计算结果与文献[7]中的结果进行对比，见图15。对于该非点源问题，改进前的四边形单元不能得到正确的结果，改进后的计算结果与文献结果吻合很好，说明对四边形单元的双线性改进处理可提高传统常应变单元方法在处理结构声耦合问题时的正确性。

3.6热应力问题

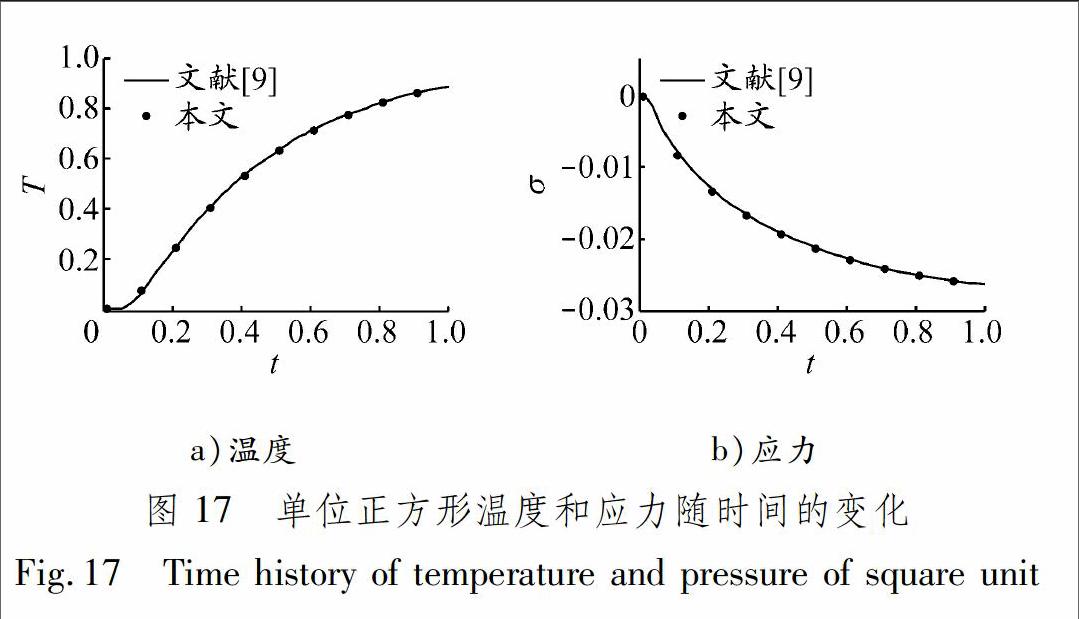
单位正方形热应力问题[8]示意见图16。计算数据进行无量纲化处理。上表面自由，温度为Tup=1，其余三边简支且绝热。采用平面应变假设，所有变量初始值均为0，时间步长为Δt=0.02。材料的杨氏模量E=1.0，泊松比μ=0.3，热导率k=1.0，密度ρc=1.0。为验证本文方法对非结构网格的适用性，采用196个三角形和98个四边形划分计算域。本文计算结果与文献[9]得到的结果对比见图17。由此可以看出，两者吻合良好，可验证本文方法的正确性。

5结束语

基于多物理场耦合问题进行计算软件研发的基本思想，介绍计算软件GTEA开发的一些实际问题及解决方法，其中包括网格格式和并行计算等问题，并通过几个具体算例展示该计算软件的功能。参考文献：

[1]雷国东， 柳贡民， 明平剑， 等. CGNS API和FVM在非结构混合网格计算中的应用[J]. 计算物理， 2007， 24（3）： 277281.

LEI G D， LIU G M， MING P J， et al. CGNS API and FVM in unstructured hybrid grid computational method[J]. Chinese Journal of Computational Physics， 2007， 24（3）： 277281.

[2]明平剑， 张文平. 计算多物理场——有限体积方法应用[M]. 北京： 北京航空航天大学出版社， 2015.

[3]明平剑， 姜任秋， 朱明刚， 等. 基于PC集群并行CFD算法实现[J]. 哈尔滨工程大学学报， 2007， 28（2）： 155160. DOI： 10.3969/j.issn.10067043.2007.02.008.

MING P J， JIANG R Q， ZHU M G， et al. Parallel CFD algorithm realization based on PC cluster[J]. Journal of Harbin Engineering University， 2007， 28（2）： 155160. DOI： 10.3969/j.issn.10067043.2007.02.008.

[4]KLEEFSMAN K M T， FEKKEN G， VELDMAN A E P， et al. A volumeoffluid based simulation method for wave impact problems[J]. Journal of Computational Physics， 2005， 206（1）： 363393. DOI： 10.1016/j.jcp.2004.12.007.

[5]MING P J， ZHANG W P. Numerical simulation of natural convection and radiation heat transfer in twodimensional enclosure on hybrid grids[J]. Numerical Heat Transfer： Part B Fundamentals， 2012， 61（6）： 505520.

[6]FU L R， ZHANG W P， MING P J， et al. Numerical method on natural convection and radiation heat transfer with an isotropic scattering medium[J]. Numerical Heat Transfer： Part B Fundamentals， 2015， 68（5）： 434458.

[7]SOARES D， RODRIGUES G G， GONALVES K A. An efficient multitimestep implicitexplicit method to analyze solidfluid coupled systems discretized by unconditionally stable timedomain finite element procedures[J]. Computers and Structures， 2010， 88（56）： 387394. DOI： 10.1016/j.compstruc.2009.12.001.

[8]BALIGA B R， PATANKAR S V. A new finiteelement formulation for convectiondiffusion problems[J]. Numerical Heat Transfer， 1980， 3（4）： 393409. DOI： 10.1080/10407798008547056.

[9]袁欣， 孫慧玉. 黏弹性树脂基三维编织复合材料的热膨胀性能研究[J]. 固体力学学报，2012， 33（4）： 379385. DOI： 10.3969/j.issn.02547805.2012.04.005.

YUAN X， SUN H Y. Study on thermal expansion properties of viscoelastic resinbased 3D braided composites[J]. Chinese Journal of Solid Mechanics， 2012， 33（4）： 379385. DOI： 10.3969/j.issn.02547805.2012.04.005.（编辑武晓英）第26卷 第6期2017年12月计 算 机 辅 助 工 程Computer Aided EngineeringVol.26 No.6Dec. 2017endprint