提高管壳式换热器温度传感器测量精度的研究

2018-01-12

自动化与仪表 2017年2期

（陕西理工大学陕西省工业自动化重点实验室，汉中 723000）

当今社会，制冷业已经成为人们生活中不可或缺的组成部分，制冷需求极速增加，给赖以生存的环境和能源带来了巨大的压力。针对目前现状，研发出了低温余热吸收式制冷机组，它利用工业中低温废气、废水作为主要驱动能源，具有很好的环保节能功效，其制冷效果也很好，在我国大中型城市得到了广泛应用。但对于低温余热吸收式制冷系统管壳式换热器的研究，最重要的就是其温度参数的测量，如果测量的温度值不准确，会影响制冷系统效率的提高。

1 Pt100温度传感器数据的标定

在众多Pt系列的传感器之中，Pt100温度传感器测量精度很高，测量范围在-40℃～+85℃之间，被广泛应用于低温余热吸收式制冷系统的发生器、吸收器中。所以检测就选用0～90℃的范围，依次改变恒温箱的温度进行检测。在实际应用中，首先对其进行R-T特性校正，常用方法有：①差值计算[1]，但是这种方法计算精度不够，必须选择合适的差值节点，而且运算时还占用很大的储存空间；②PB运算[2-4]，这种方法收敛速度慢，容易陷入局部极小而得不到全局最优值，计算结果误差太大，对于网络的隐节点数选取没有理论指导；③硬件补偿运算[5-6]，这种方法是对其测量电路进行校正补偿，虽然精度高，但操作复杂，而且电路中的元器件操作不当容易相互干扰，在实际生产中得不到广泛应用。

为了保证数据的拟合精度和直接有效地查看拟合效果，利用最小二乘法将测量数据分成3段，分别进行一次、二次、三次拟合，该方法拟合出的校正方程简单易懂，在对低温余热吸收式制冷系统和误差分析的应用中证实该方法测量精度非常高。低温余热吸收式制冷系统的吸收器、发生器研究的温度范围通常是在0～90℃，所以可以在这个监测范围内进行测试，采用恒温箱控制温度，依次改变恒温箱温度进行测量，采用四线制结法对Pt100温度传感器进行连接，用安捷伦表对Pt100铂电阻随温度变化而对应的电阻值进行测量，用精度高的数字温度计测量它的实际温度，图1所示为测量的实际数据。

图1 Pt100温度传感器R-T的实测数据的关系曲线Fig.1 R-T curve of measured data of the Pt100 tempreature sensor

由图1曲线可看出Pt100温度传感器具有非线性的特性，由此引出传统的校正方程，由文献[7]可知，Pt100温度传感器的温度和电阻关系在0～850℃范围之间的校正方程为

式中：Rt为温度t时的电阻；R0为t=0℃时的电阻；A=3.90802×10-3℃-1；B＝-5.801×10-7℃-2。本文将实测数据分成（0～30 ℃）、（30～60 ℃）、（60～90 ℃）3 个区间，用最小二乘法对区间内的数据进行一次、二次、三次拟合，然后利用误差评估原理得出Pt100温度传感器最佳的校正方程。

2 基于Matlab的数据拟合方法

2.1 最小二乘法拟合原理

首先测出一组数据（xi， fi）（i=0，1，2，3，4，…，n），找出一条最佳的拟合曲线y（x），使曲线上的各点的值y（xi）与测量值 fi的差的平方和在所有的拟合曲线中最小[8-10]。

设因变量 fi与 m 个自变量 x1，x2，x3，…，xm之间的关系为

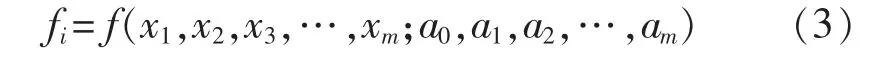
式中：a0，a1，a2，…，am为 m+1 个待定系数。

从而有

则有方程组：

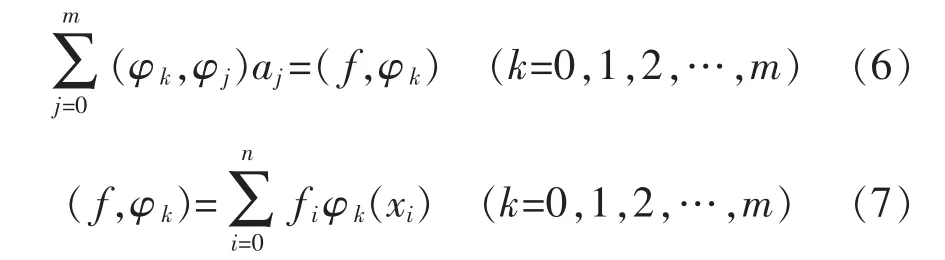
用矩阵形式表示为

求解以上的矩阵方程可得 a0，a1，a2，…，am。

2.2 利用Matlab实现

Matlab中的内置函数polyfit可以进行n次多项式拟合[11-12]，其调用格式为

式中：X为测量的温度；Y为其所对应的电阻值；n为多项式的次数。

在（0～30 ℃），（30～60 ℃），（60～90 ℃）区间内分别进行一次、二次、三次拟合，拟合后的多项式为

（1）一次拟合多项式

（2）二次拟合多项式

（3）三次拟合多项式

分段拟合后的图形如图2所示。

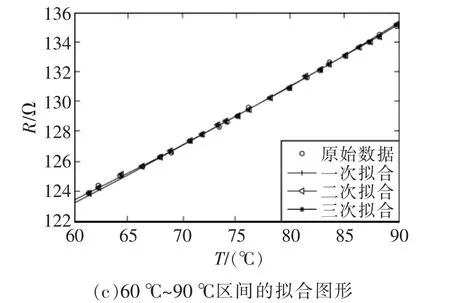
图2 最小二乘法的分段拟合图形Fig.2 Schemes of the segment fitting least square method

2.3 误差分析原理

测量温度和电阻值的时候，有效数字的位数虽然一点，但也会出现测量误差；拟合中选取精确度时，也会造成一些误差。本文通过绝对误差，标准误差以及算数平均误差来比较实测数据与拟合图形之间的误差[13-14]。

2.3.1 绝对误差

式中：di为校正方程的绝对误差，di波动越小，校正方程精度越高；yi为实测值；f（xi）为各个拟合关系式的拟合值。

2.3.2 算术平均误差

式中：δ为校正方程的算数平均误差，δ越小，精度越高；n为实测数据点数。

2.3.3 标准误差

式中：σ为校正方程标准误差，σ越小，精度越高，拟合度也越高。

2.4 评价校正方程

经过对各段拟合方程的系数进行误差分析，可知 Pt100温度传感器分别在（0～30℃，30～60℃，60～90℃）区间内进行一次拟合时的误差震荡波动最大，二次次之，三次拟合误差相对较小，通过对二次，三次2种拟合进行标准误差及算术平均误差的对比，可以得出Pt100温度传感器的最佳校正方程，结果如表1所示。

由表 1可以看出在 0～30℃，30～60℃，60～90℃区间上，三次拟合方程拟合出来的数据最小，精度最高，逼近度最高。所以在0～90℃区间内，与Pt100温度传感器R-T的实测数据的逼近度最高的是三次拟合方程，故最佳校正方程为

表1 Pt100温度传感器在0～90℃区间方程拟合误差Tab.1 Equation fitting error of Pt100 temperature sensor at 0～90 ℃

3 结语

本文利用最小二乘法对Pt100温度传感器的实测数据进行分段拟合得出了温度与电阻间的关系式，对低温余热制冷系统的温度控制意义重大。通过对绝对误差，算术平均误差以及标准误差的综合分析，得出在0～90℃区间内，三次拟合方程与Pt100温度传感器R-T的实测数据的逼近度最高。经过实验测量计算验证，得到校正方程比传统方程提高了2个数量级，符合其测量精度的需求。本文确定校正方程的方法不仅适用于Pt100温度传感器，而且也适合各类热电阻温度传感器的校正拟合。

[1]刘少强，黄惟一.基于插值计算与优化的铂电阻非线性校正方法[J].仪器仪表学报，2003，24（2）：216-219.

[2]孙毓星，洪学文，王卓军.铂电阻温度传感器的线性化方法[J].测控技术，1989（2）：34-39.

[3]刘天键，王劭伯，朱善安.基于神经网络的铂电阻温度传感器非线性校正方法[J].仪器仪表学报，2002，23（5）：81-84.

[4]李琴，刘海东.改进BP网络及其在传感器非线性校正中的应用[J].计算机应用与软件，2009，26（7）：181-184.

[5]张修太，胡雪惠，翟亚芳，等.基于PT100的高精度温度采集系统设计与实验研究[J].传感技术学报，2010，23（6）：813-815.

[6]张志勇，辛长宇，朱玉龙，等.Pt100温度传感器非线性的补偿方法与电路实现[J].电子器件，2007，30（6）：2190-2191.

[7]工业铂、铜热电阻JJG229-1998[S].北京：中国计量出版社，2004.

[8]向军文.最小二乘法在定向钻进中的数据拟合[J].石油钻采工艺，2010，32（6）：16-18.

[9]陈岚峰，杨静瑜，崔崧，等.基于MATLAB的最小二乘曲线拟合仿真研究[J].计算机与现代化，2014，32（1）：75-78．

[10]杨大地，王开荣.数值分析[M].北京：科学出版社，2006.

[11]杨云升.Matlab曲线拟合及其在试验数据处理中的应用[J].电脑与信息术，2009，17（2）：35-36.

[12]赵海滨.Matlab应用大全[M].北京：清华大学出版社，2012.