遗传算法优化BP神经网络的粒径大小研究

（兰州理工大学 电气工程与信息工程学院，兰州 730050）

在片剂生产行业流传着“制粒是龙头，压片是核心，包衣是凤尾”这样一句话，可见药物的湿法制粒工段在整个工序中起着举足轻重的作用。第一道工序的好坏影响着后面其他工序的生产质量，其中所得颗粒的的平均粒度是该工段的重要参数之一，粒度分布越集中，颗粒含量均匀度差异就小，颗粒的休止角小，实际的压片过程中模圈填料均匀保证较小的片重差异，与此同时颗粒的平均粒径对片剂的硬度也有较大的影响，粒径相对小时片剂具有较高的硬度。一般情况下粒径大小越集中于40～60目亦即 250 μm～420 μm，所得颗粒越合乎生产要求[1]。

本文以浙江某制药设备公司的一新型高效湿法制粒机为研究对象，该设备一开始试运行阶段所得药物颗粒的粒径大小始终不能满足生产要求。通过分析得知影响颗粒平均粒径大小的主要因素有搅拌桨转速、切割刀转速、搅拌时间、切割时间，而该4个因素与颗粒平均粒径之间呈非线性函数关系，建立数学模型十分困难[2]。因此，根据系统的输入输出关系构建一合理的BP神经网络，用来拟合平均粒度大小与搅拌桨转速、切割刀转速、搅拌时间、切割时间非线性函数关系。此外，为避免BP神经网络由于初始权值、阈值的随机选取而导致的易陷入局部极值点而得不到全局最优解的缺点，利用遗传算法优化构建好的BP神经网络，从而实现对平均粒径大小与其影响因素关系的非线性拟合，最终实现对平均粒径的理想控制。

1 BP神经网络介绍

BP（back propagation）神经网络是J.LMcClelland和D.E.Rumelhart于1986年提出的一种借用误差反向传递训练算法的有隐含层的多层前馈网络[3]。网络根据系统的输入输出关系数据经过相应的网络训练可以有效地建立输入输出之间的任意非线性映射关系，实现目标值与各个影响因子之间的内在联系[4]。

BP算法的实现实际上包括2个阶段：正向传播阶段和反向传播阶段。在正向传播过程，输入信息从输入层输入，然后经过隐含层处理，最终由输出层传出。这个过程中上一层节点输出传送至下一层，并通过调整连接权系数Wij来达到增强或者消弱上层输出的作用。输出层和隐含层每一个节点的输入是前一层节点输出的加权和，每个节点的激活程度由它的输入信号、节点阈值、以及激活函数决定。输入层节点的输出等于其输入。在反向传播过程，如果BP神经网络的输出层得不到预期的输出值则进入反向传播，该过程将网络的期望输出与实际输出的差值即误差信号沿原来的连接通道返回，并逐层修改各个神经元的权值和阈值，使得误差信号最小。BP神经网络结构如图1所示。

2 遗传算法介绍

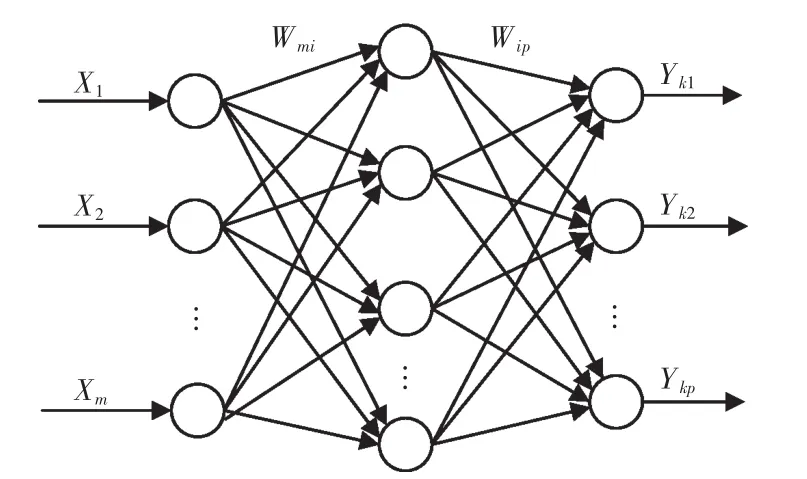
图1 BP神经网络结构Fig.1 BP neural network structure diagram

遗传算法（genetic algorithms）是美国Michigan大学教授Holland于20世纪60年代提出的一种模拟自然界的生物进化论和遗传机制而发展起来的基于自然选择和基因遗传思想的一种高效启发、并行计算随机搜索最优化方法，其来源于达尔文的进化理论以及孟德尔的群体遗传学说。该算法的基本思想是将自然界的优胜劣汰，适者生存的生物进化理论引入优化参数形成的编码串群体中，种群个体根据选择的适应度函数在通过遗传中的选择、交叉、变异操作后进行逐个筛选，最终淘汰适应度值较差的个体，保留适应度值较好的个体。这样所得的新的种群不仅遗传了上一种群的信息，又优于上一种群。反复进行遗传操作，直至满足条件要求的新群体产生。遗传算法从根本上说就是模拟生物界的进化机制与过程求解极值问题的一类自组织自适应人工智能技术[5]。

遗传算法的基本算法实现是从代表问题潜在的解集的一个种群开始的，将这些解集的每个个体通过实数编码或者二进制编码等方法转换成由一定数目染色体组成的种群。初代种群产生后，在种群内部按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解。在每一代，根据问题域中个体的适应度值大小选择个体，并借助于自然遗传学的遗传算子进行遗传操作。通过选择操作将种群中优良个体即个体适应度值符合要求的个体遗传到下一代的种群中。利用交叉操作，进行种群中个体染色体即编码串的重组来产生新的个体。利用变异操作实现染色体的点上变异得到优秀个体从而实现种群向更好的方向进化。这个过程将导致“编码串种群”像自然进化一样，后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。遗传算法流程如图2所示。

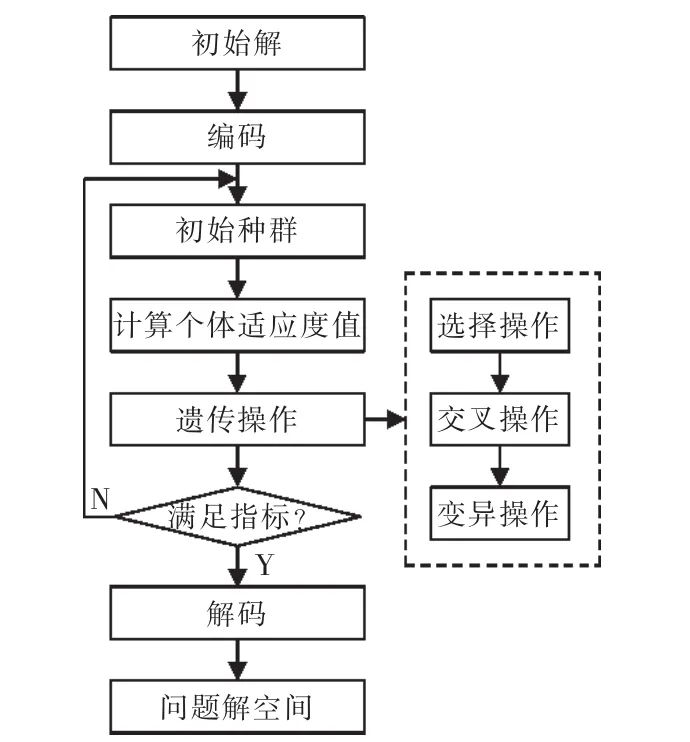
图2 遗传算法流程Fig.2 Genetic algorithm flow chart

3 BP网络算法实现

基于遗传算法优化BP神经网络的算法流程如图3所示。

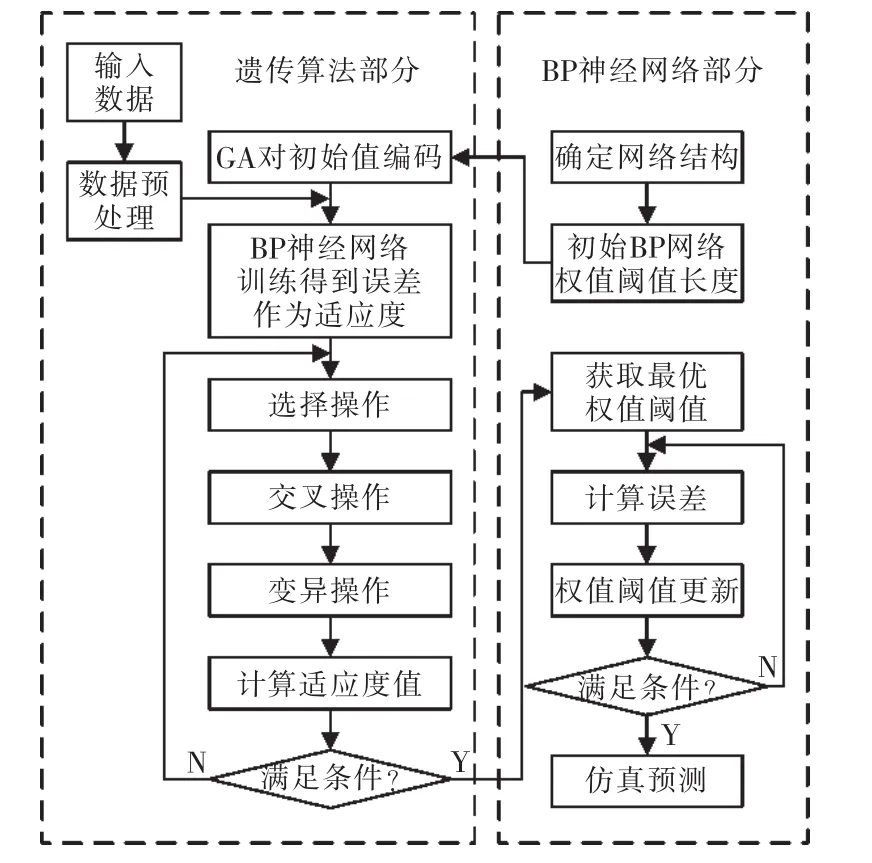
图3 遗传算法优化BP神经网络算法流程Fig.3 Genetic algorithm optimize BP neural network algorithm flow chart

3.1 BP网络参数设计及网络实现

根据Kolmogorvo定理，三层BP神经网络充分学习后能逼近任何函数。因此对于一般问题通常选择含有一层隐含层的BP神经网络作为实验的网络结构，必要时也可通过增加隐含层的神经元个数来降低误差。

（1）湿法制粒阶段所得颗粒的平均粒径影响因素包括搅拌桨转速、搅拌时间、切割刀转速、切割时间4个因素。所以确定输入层神经元的个数为4。输出层控制变量仅为平均粒径的大小，所以输出层神经元个数为1，其传递函数为线性函数purelin。隐含层神经元个数的选取为首先根据式（1）确定一数值，再经过多次实验仿真最终确定隐含层神经元个数为9个。隐含层神经元的传递函数为tansig函数。

（2）数据的归一化处理是把所有输入层数据转化成［0，1］之间的数。在BP神经网络中输入层的每一个维度代表一个特征，当输入层含有多个神经元即为多维度输入时就要取消各个维度数据之间的数量级差别。避免因输入的数据数量级别差距较大使得某些数值低的特征被淹没从而导致网络预测误差较大的情况发生。对BP神经网络数据进行归一化处理一般采用最大最小法，其函数形式为

数据的反归一化处理为归一化处理的反过程，输出的数据只有经过反归一化处理才能得到所需要的数据。

（3）BP神经网络的训练就是根据系统的输入，输出数据神经网络，使得经训练所得的BP网络能够预测系统的输入输出。根据高效湿法制粒机的实际生产采样1000组输入输出数据，选取其中800组作为网络的训练数据，余下200组作为测试数据，验证网络的拟合能力。

（4）BP神经网络的预测就是用训练好的BP网络预测系统的输出，对照实际输出对预测的结果进行分析，验证BP网络的优劣。

进行BP神经网络的Matlab仿真，选择网络的迭代次数为100，误差精度为0.01，学习速率为0.4。最终所得实验仿真结果如图4所示。

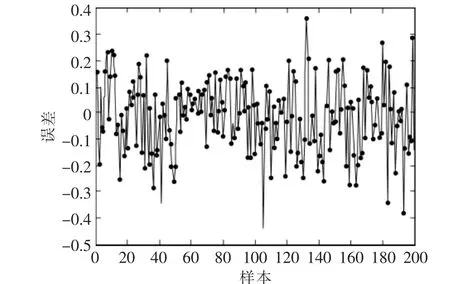
图4 BP神经网络预测误差Fig.4 BP neural network predicted error diagram

3.2 遗传算法优化BP神经网络

BP神经网络虽然具有较高的拟合能力，但网络预测误差仍然较大，因为BP神经网络的初始权值和阈值的选取过于随机，导致网络容易陷入局部最优。因此可以将BP神经网络和遗传算法结合起来，用遗传算法找出BP网络的最优初始权值和阈值，这样就可以弥补初始权值和阈值随机取值导致的缺陷，从而使得网络的预测精度更高[6-7]。

（1）种群初始化，随机生成M个个体，每个个体的长度由BP网络的结构确定。其中每个个体包括了BP网络所有的权值和阈值，作为遗传算法进化过程的起点。

选取种群规模时如果群体的规模过小，会导致群体中个体的多样性降低，限制遗传算法的搜索空间范围，导致算法陷入局部最优解而得不到全局最优解。与之相反，群体规模越大，算法陷入局部解的危险性就会越小。但是规模过大会增加算法的计算量。最终我们选取遗传算法的种群规模为30。

（2）编码采用实数编码方法，编码顺序为从输入层到输出层，从权值到阈值的方法。由上节仿真得知BP网络输入层、隐含层输出层的神经元个数分别为4、9和1。编码串的总长度计算公式为

因此可得编码串总长度为55。

（3）适应度函数的选取，选取网络误差函数作为适应度函数。并根据每个个体的适应度进行选择操作、交叉操作和变异操作。

变异概率一般较小，仍必须适当选择，因为如果过大虽然会增加样本的多样性，但会引起整个系统的不稳定。交叉概率决定了交叉操作的频率，该数值越高，算法收敛到最优解区域的速度越快。一般情况下交叉概率的选取范围为0.4～0.9。通过反复试验确定选定交叉概率为0.4，变异概率为0.02。

（4）进化若干代数后，当种群的平均适应度不再发生变化后则停止进化，否则重复第二步与第三步操作，最终的仿真结果如图5、图6所示，预测效果对比如表1所示。

遗传算法优化BP神经网络最终网络预测误差更加精确，其预测成品率和实际成品率之间的最大误差只有0.03 mm，具有相对良好的拟合性。对实际生产具有一定的指导意义。最终利用遗传算法寻优的湿法制粒所得颗粒平均粒度在40～60目的最佳参数组合为搅拌机转速为1400 r/min，搅拌时间为220 s，切割刀转速为3000 r/min，切割时间为240 s。

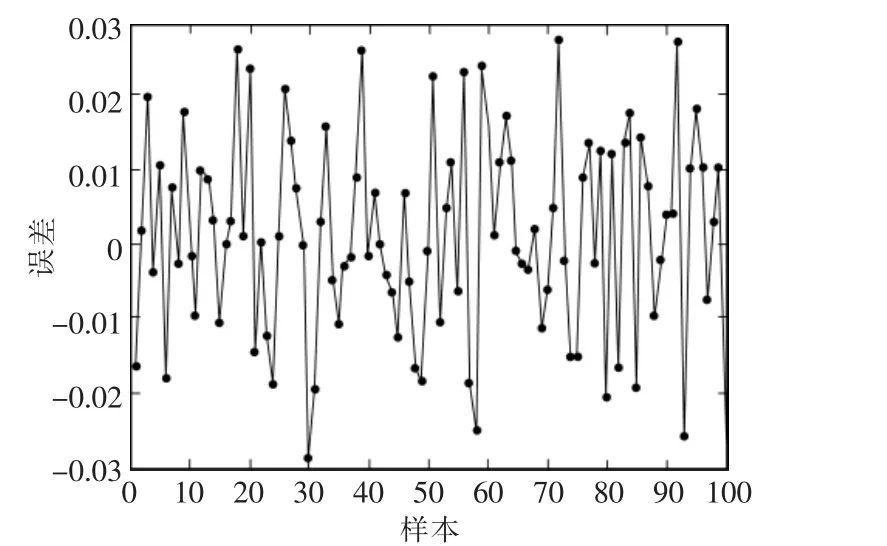
图5 遗传算法优化BP神经网络误差Fig.5 Genetic algorithm optimize BP neural network error diagram

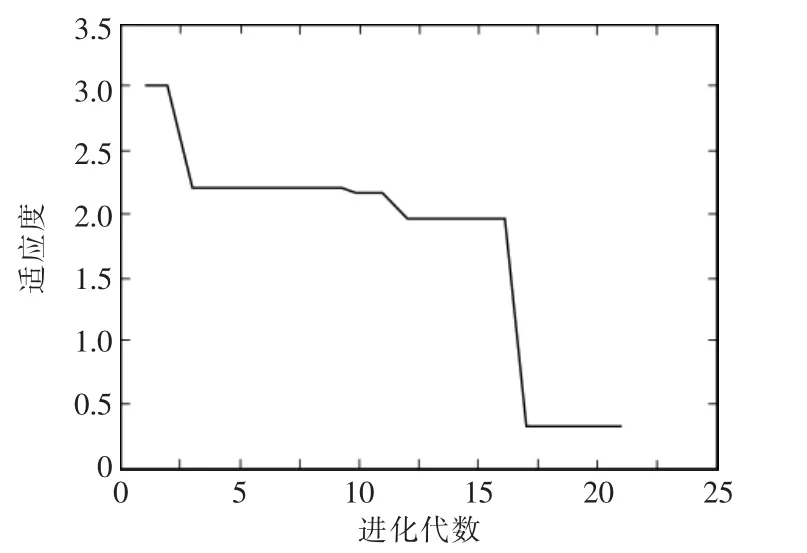
图6 最优个体适应度Fig.6 Fitness of optimal individual diagram

表1 预测效果对比Tab.1 Comparison of predicted effects

4 结语

BP神经网络虽然具有较高的拟合能力，但网络预测误差仍然较大的主要原因为BP神经网络的初始权值和阈值的选取过于随机，导致网络容易陷入局部最优值。因此，可以将BP神经网络和遗传算法结合起来，用遗传算法找出BP网络的最优初始权值和阈值，这样就可以弥补初始权值和阈值随机取值导致的缺陷，从而使网络的预测精度更高[5]。

拟合湿法制粒机运行过程中搅拌速率、搅拌时间、切割速率、切割时间与平均粒径之间的非线性函数关系，得到湿法制粒机运行过程中搅拌速率、搅拌时间、切割速率、切割时间的最佳运行参数。这些参数会保证所制颗粒的良好粒径分布，从而最终提高片剂的生产率以及质量，其设计思路具有一定的借鉴价值。

[1]张毓，钟晓明.中药颗粒成型工艺的研究进展[J].海峡药学，2010，22（1）：27-30.

[2]李奉勤，史冬霞，马震嗣，等.正交设计在中药制粒工艺研究中的应用概况[J].中国药业，2006，15（3）：67-68.

[3]王晓红.基于遗传神经网络中药片剂生产过程控制研究 [D].江西：南昌航空大学，2012.

[4]刘洁，刘子龙.典型非线性系统的自适应BP神经网络跟踪控制器设计[J].自动化与仪表，2004，19（2）：12-15.

[5]孙自广，李春贵，王秦.基于改进遗传算法的机器人路径规划[J].自动化与仪表，2009，24（6）：5-7.

[6]刘占明.基于案例推理和智能算法的石漠化治理模式优选研究[D].广西：广西师范学院，2011.

[7]徐齐胜，罗胜琪，陶欣，等.基于神经网络遗传算法的锅炉燃烧优化系统[J].自动化与仪表，2014，29（6）：30-32.