从单摆到微分方程近似解的新解法

从高中物理教材对单摆简谐性质的介绍出发，更深一步认识简单的摆的运动性质和视为简谐运动的条件，联系单摆作为计时器件的不足。通过用不同方式化简微分方程和使用计算机计算数值解并绘图，针对单摆模型的理论计算和现实中的摩擦阻尼试进行进一步讨论。

在高中物理选修课上我们已学习过单摆系统在小角度擺动的条件下可以近似为简谐运动，并了解了通过单摆测量当地重力加速度的值；在实验中，我们得到了与实际值较为符合的实验结果，可见这样的近似是合理的。然而，在实际生活中摆角并不能做到很小，否则单摆的能量很快回衰减到0，同时也会给测量上带来困难。因此在实际生活中，单摆的周期存在一定的误差，进一步计算表明，当摆角为5°时周期误差小于0.5%。本文讨论单摆在非小角度情况下的运动规律，得到非小角度下单摆周期的修正公式，并以此为基础讨论其在实际生活中的应用。诚然，单摆作为力学经典模型之一，其理论和各个方向的应用早已被讨论透彻，但从学生的角度还有一些东西可以发掘探究。

求理想模型中单摆的周期

初解方程

假设单摆长l，小球质量为m，初始摆角为α，空气摩擦不计。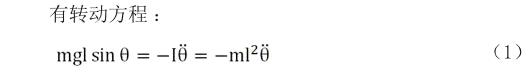

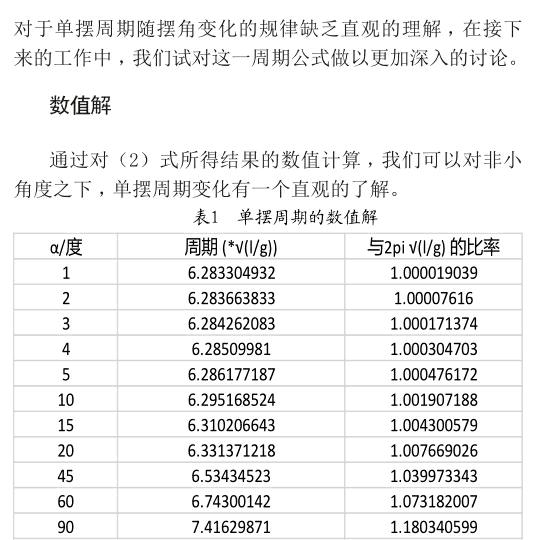
从表中我们可以看到，当单摆的摆角增大时，单摆周期也随之增大，并且偏差有加速增加的趋势。

修正周期公式

1）通过待定系数求解。

单摆在任意位置的运动状态都是确定的，因此即使在大角度下单摆依旧做周期运动，只是周期和周期内角度关于时间的分布有所改变。因此，我们不妨假设新的单摆仍做简谐运动，并通过待定系数法求解使得在某一最大摆角下最贴近真实运动的ω。

可以看到，待定系数方法修正的结果与实际情况最为接近，即使在60度的摆角之下，依然和数值解符合的很好。而高阶小量修正法的结果更加简洁明了，易于应用。另外，在“通过高阶小量展开近似求解”的讨论中，我们将其（1）的式子展开到二次项，但只将其（2）的式子展开一次项，结果却发现后者更精确，这也是很有意思的。

在实际中的应用

摆钟很早就被广泛应用于实际生活中。如果不能够充分考虑较大摆角下面周期变化，可能使得摆钟有较大的误差。

考虑空气阻力

定性分析：在一个单摆周期中，空气阻力产生的作用大约一半朝正放向，一半朝负方向，但总阻碍小球摆动。鉴于空气阻力始终与单摆运动方向相反，因此可以预见，由于空气阻力的存在，单摆的周期会有所变长。同时，当小球质量不太小，最大速度不太大时，系统在一个适合观察的时段内摆动幅度缩小不太过明显，可近似认为做周期运动。

对此方程，在各项数值确定的情况下可以方便地通过计算机做出将来的运动图像，由此即可与理想状况进行比较。

其他在单摆中存在而能够被忽略或较难以研究的因素

考虑地球引力场是有心力场；考虑地球参考系中由地球自转产生的科里奥利加速度；悬绳所挂节点在多次扭转过程中产生的热量损失；绳能被视作具有非常大劲度系数的弹性绳等。

结论

虽然单摆在实际生活中的作用已经逐渐减小，但是在单摆求解过程中的思考却可以给我带来很多启发。本文从单摆的大角度求解出发，从数值求解，泰勒展开求解以及待定系数优化误差三个角度分别讨论了单摆在大角度情况下周期的变化，并验证了，我们所提出的泰勒展开法与待定参数法所得到的结果与实际结果在60度的大摆角的情况下依然相当吻合。

同时基于误差最小优化参数的方法是我们独立提出的具有创新性的一种微分方程的新解法，这对微分方程近似解求解有着积极的指导作用。

参考文献

[1]刘凤祥.单摆运动周期的近似解[J].大学物理，1999，18（11）：5-7.

[2]黄秀兰.单摆周期近似解的讨论[J].云南师范大学学报（自然科学版），1995（2）：38-45.

[3]谭志忠.求大摆角单摆周期近似解的“局部常化”方法[J].大学物理，2005，24（12）：14-17.

（作者简介：朱嘉玮，江苏省丹阳高级中学。）endprint