广义变分不等式组和非扩张映射对的Wiener-Hopf方程技巧

邱洋青

(上海第二工业大学理学院,上海201209)

广义变分不等式组和非扩张映射对的Wiener-Hopf方程技巧

邱洋青

(上海第二工业大学理学院,上海201209)

将含松弛共强制映射的广义变分不等式组和非扩张映射对转化为广义非线性Wiener-Hopf方程组,构造新的迭代算法,证明广义变分不等式组解集和非扩张映射对积集公共解的存在性及迭代序列的强收敛性。

Wiener-Hopf方程技巧;松弛共强制映射;迭代算法;非扩张映射

0 引言

将变分不等式转化为算子方程,最终化为不动点问题,是求解变分不等式普遍使用的方法,其中之一是将变分不等式转化为Wiener-Hopf方程[1-9]。设H是实Hilbert空间,C⊂H为非空闭凸子集,C(H)是H中所有非空紧子集的全体,Ai:C×C→H是非线性映射,Bi:H×H → C(H)是集值映射,i=1,2。寻找(x,y)∈C×C,w1∈B1(x,y),w2∈B2(x,y),使得

式(1)称为广义变分不等式组,它的解记为SVI(C,Ai,Bi)。又设S1,S2:C→C是2个非扩张映射,它们的不动点集的积集记为F(S1)×F(S2)。设SVI(C,Ai,Bi)∩(F(S1)×F(S2))非空,本文将Wiener-Hopf方程技巧用于求解广义拟变分不等式组解集和非扩张映射对不动点积集的公共解问题,是文献[1-9]中主要结果的整合、改进和推广。

若A1=A2=A,B1=B2=B,则式(1)化为:找x∈C,w∈B(x)使得

它是由Noor[1]引进并研究的。

1 预备知识

定义1[5,10]设X是自反Banach空间,T :X →X∗是单值映射,如果存在2个常数α,β＞0,使得

其中D(T)表示T的定义域,G(T)表示T的图,则称T为(α,β)-松弛共强制的。

引理1[11]设H是Hilbert空间,C是H的非空闭凸子集,PC表示H到C上的投影算子,给定点z∈H,则∀x∈C满足不等式

当且仅当

引理2[11]由引理1定义的投影算子PC:H→C是非扩张的,即

‖PC(u)-PC(v)‖ ≤ ‖u-v‖, ∀u,v ∈ H

引理3 (x,y,w1,w2)是式(1)的解当且仅当(x,y,w1,w2)满足

式中:(x,y)∈C×C,w1∈B1(x,y),w2∈B2(x,y),PC是H 到C上的投影算子;ρ1,ρ2＞0是常数。

证明 由引理1即得。

2 Wiener-Hopf方程技巧及迭代算法

建立Wiener-Hopf方程。

设I是H中的恒同映射,令QC=IPC,S1,S2:C → C是非扩张映射,寻找z1,z2,w1,w2∈ H,使得w1∈ B1(PCz1,PCz2),w2∈B2(PCz1,PCz2)且

称为广义非线性Wiener-Hopf方程组。

值得注意的是:当B1=B2,S1=S2=I时,即为 Wiener-Hopf方程[1-3]。

定理2 广义变分不等式组式(1)的解集和非扩张映射对不动点积集存在公共解(x,y)∈SVI(C,Ai,Bi)∩(F(S1)×F(S2))当且仅当广义非线性Wiener-Hopf方程组(4)有解,(x,y)∈C×C,(z1,z2)∈H×H,w1∈B1(PCz1,y),w2∈B2(x,PCz2),且满足

式中,ρ1,ρ2＞ 0 是常数。

证明 (1)必要性。若(x,y)∈SVI(C,Ai,Bi)∩(F(S1)×F(S2)),则x=S1x,y=S2y。又由引理3可知,(x,y)满足式(3)。令z1=x-ρ1(A1(x,y)+w1),z2=y-ρ2(A2(x,y)+w2),则由式(3)知,x=PCz1,又x=S1x,可得x=S1PCz1。同理,由y=S2y和y=PCz2可得y=S2PCz2,从而式(5)成立,且

上式就是广义Wiener-Hopf方程组(4)。

(2)充分性。由上述过程反推即得。定理证完。

利用定理2,构造以下迭代算法:

算法1 设Ai:C×C→H,Bi:H×H→C(H),S1,S2:C→ C是非扩张映射对,任意∈B1(x0,y0),∈B2(x0,y0),由以下迭代程序

式中,n=0,1,···。

3 主要结果

下面求解广义变分不等式组解集和非扩张映射对不动点积集的公共逼近解。

定理3 设H是实Hilbert空间;C⊂H为非空闭凸子集;S1,S2:C → C是非扩张映射;Ai:C × C → H 是 (ξi,ηi)-Lipschitz连续且关于第i变元是(αi,βi)-松弛共强制映射;Bi:H×H→C(H)是(γi,ζi)-˜H-Lipschitz连续映射,i=1,2。若

由式(8)有

由A1关于第一变元的松弛共强制(见定义1)及Lipschitz连续性,有

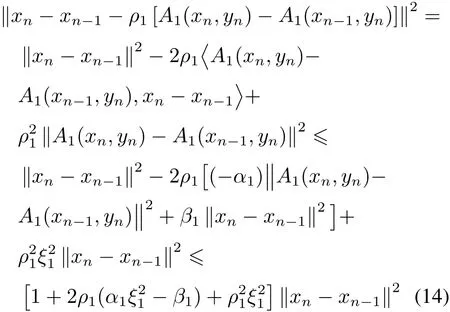
及

由式(10)及B1的˜H-Lipschitz连续性,有

由式 (13～16)有

同理有

又由式(6～7)及引理2有

和

由式 (17～20)有

式中

其次,由式(19～20)知,{xn},{yn}也是H中的Cauchy列,从而存在x∗,y∗∈H,使得当n→∞时,xn→x∗,yn→y∗。由式(16)可知,{}也是H 中的Cauchy列。同理,{}也是H中的Cauchy列。

因为B1(x∗,y∗)是紧集,所以∈B1(x∗,y∗)。同理可得,∈B2(x∗,y∗)。由PC,A1,A2的连续性及式(6～9),令n→∞,有

即式 (5)成立。从而由定理 2,有 (x∗,y∗) ∈SVI(C,Ai,Bi)∩(F(S1)×F(S2))。定理证完。

注1 定理3研究的是广义变分不等组解集与非扩张映射对不动点积集的公共元问题,是文献[5～7]中所研究问题的推广。具体来说,文献[5]研究的是变分不等式组问题,文献[6～7]研究的是一个变分不等式的解和一个非扩张映射不动点的公共元问题。

若A1=A2=A,B1=B2=B,S1=S2=I,由算法1,为式(2)构造相应的迭代算法:设A:C→ H,B:H→ C(H),任意给定z0∈H,x0=PCz0,w0∈B(x0),由以下迭代程序得到序列{xn}、{zn}和{wn}。

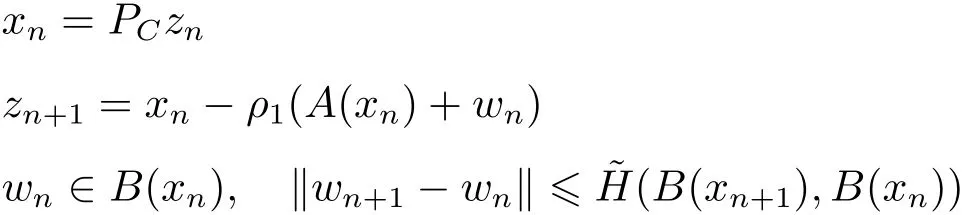
其中 n=0,1,···。

由定理 3,αi= ηi= ζi=0,ξ2= γ2=0,即有以下结论:

推论1 设H是实Hilbert空间,C⊂H为非空闭凸子集,A:C→H是β-强单调ξ-Lipschitz连续映射,B:H→C(H)是γ-˜H-Lipschitz连续映射,若ρ满足以下条件:

则 存 在 (x∗,w∗) 是 式 (2)的 解,z∗满 足 相 应的Wiener-Hopf方程,且由新算法生成的序列{xn},{zn},{wn} 分别强收敛于 x∗,z∗,w∗。

[1] NOOR M A.Some developments in general variational inequalities[J].Applied Mathematics&Computation,2004,152(1):199-277.

[2] SHI P.Equivalence of variational inequalities with Wiener-Hopf equations[J].Proceedings of the American Mathematical Society,1991,111(2):339-346.

[3] NOOR M A.Wiener-Hopf equations and variational inequalities[J].J Optim Theory Appl,1993,79(1):197-206.[4] NOOR M A.Iterative schemes for multivalued quasi variational inclusions[J].J Global Optim,2001,19(2):141-150.

[5] QIU Y Q,LI X L.The existence of solutions for systems of generalized set-valued nonlinear quasi-variational inequalities[J].Fixed Point Theory&Applications,2013(1):1-15.

[6] NOOR M A,HUANG Z Y.Wiener-Hopf equation technique for variational inequalities and nonexpansive mappings[J].Applied Mathematics&Computation,2007,191(2):504-510.

[7] QIN X L,NOOR M A.General Wiener-Hopf equation technique for nonexpansive mappings and general variational inequalities in Hilbert spaces[J].Applied Mathematics&Computation,2008,201(1/2):716-722.

[8] 闻道君,宋树枝,龙宪军.非凸变分不等式和非扩张映象的Wiener-Hopf方法[J].云南大学学报(自然科学版),2012,34(1):5-8.

[9] 王月虎,张从军.广义均衡问题旳算法及强收敛性——基于Wiener-Hopf方程技巧[J].数学物理学报,2015,35A(4):695-709.

[10]邱洋青,刘理蔚,兰丽英.一类新的含(A,η)-增生算子的广义混合拟-似变分包含组[J].应用泛函分析学报,2011,13(4):375-382.

[11]张石生.变分不等式和相补问题理论及应用[M].上海:上海科技文献出版社,1991.

The Wiener-Hopf Equation Technique of a System of Generalized Variational Inequalities and a Couple of Nonexpansive Mappings

QIU Yangqing
(School of Science,Shanghai Polytechnic University,Shanghai 201209,China)

A system of generalized variational inequalities involving relaxed co-coceive mappings and a couple of nonexpansive mappings were transferred into the system of generalized Wiener-Hopf equations.A new iterative algorithm was constructed.Finally,the existence of the common solution of the system of generalized variational inequalities and the couple of nonexpansive mappings and the strong convergences of iterative sequences were proved.

Wiener-Hopf equations technique;relaxed co-coceive mappings;iterative algorithms;nonexpansive mapping

O 177.91

A

1001-4543(2017)04-0291-04

10.19570/j.cnki.jsspu.2017.04.007

2017-07-13

邱洋青(1981–),女,江西赣州人,讲师,博士,主要研究方向为变分不等式及相补理论。E-mail:yqqiu@sspu.edu.cn。

上海第二工业大学校基金(EGD17XQD04)资助