求解一类交界面问题的模态基函数谱元法数值实验

邵文婷

(上海第二工业大学理学院,上海201209)

求解一类交界面问题的模态基函数谱元法数值实验

邵文婷

(上海第二工业大学理学院,上海201209)

采用模态基函数形式下的谱元法,对一类一维和二维交界面问题进行了数值计算研究。不仅考虑了具有间断系数的方程,还涉及了右端带有奇性源项的方程。对于二维问题的数值计算,研究了四边形单元谱元法和三角单元谱元法的离散格式。通过一些具有精确解的数值算例,验证了基于模态基函数谱元法求解交界面问题的可行性和有效性。与其他数值方法相比,谱元法对于一维问题可以实现指数阶收敛精度,对于二维问题也得到了较高的计算精度。

谱元法;四边形单元;三角单元;交界面问题;间断系数;奇性源项

0 引言

具有间断系数或者右端带有奇性源项的方程称为交界面问题。这类问题起源于许多应用领域,例如2种不同材料或者相同材料在不同状态下物理机制的研究[1]。由于方程所含的奇性,使得真解的光滑性较差,甚至在求解区域内部会出现函数值间断面。尽管在有限元、有限差分和有限体方法上,目前已提出了不少有效的数值离散格式,但对于高精度数值方法,如谱方法和径向基函数方法在这类问题上的计算研究工作并不多见。Jung等[2]提出了基于最小二乘的Legendre谱配点法和径向基函数方法来求解一维椭圆交界面问题。

对于谱方法或者拟谱方法,早期的工作[3]主要集中在单个区域上的Chebyshev谱方法和Fourier谱方法。由于这些高精度方法本身在建立离散格式时采用的基函数为定义在整个计算区域上的正交多项式,因此对真解在求解区域上局部呈现奇性的问题并不适用,对光滑性较差的函数的展开逼近具有一定的局限性。另一方面,由于本文所考虑的问题真解在物理区域交界面处具有奇性,从而破坏了光滑性,使得采用基于全局逼近的谱方法在进行数值计算时得不到指数阶收敛精度。近年来,不少计算数学研究者致力于研究适用于多个区域上进行求解的高精度方法。谱元法(SEM)[4]正是在这种迫切需求下产生的,它将有限元法的灵活网格剖分技术融合于谱方法中,使得谱方法不再局限于整体逼近,对问题的真解在局部区域上呈现不同性态时也可以进行计算,同时保留指数阶收敛精度。谱元法不仅保留了谱方法的高精度优势,同时具备了有限元法强健的区域适应性。其基本想法是将求解区域剖分成若干个互不重叠的子单元,在每个单元上采用谱方法进行离散。同有限元法类似,将单元刚度和质量矩阵按一定的顺序集成总体刚度和质量矩阵,最后求解离散得到的线性代数方程组。根据基函数的选取,SEM分为2种形式:节点基函数[5]和模态基函数[6]。有别于选取Gauss-Lobatto-Legendre(GLL)积分节点或者Chebyshev积分节点上建立的Lagrange多项式型节点基函数,模态基函数是采用Legendre正交多项式和自然定义在三角区域上的Dubiner正交多项式[7],分别建立四边形单元谱元法(QSEM)和三角单元谱元法(TSEM)。模态基函数相对于节点基函数的优势在于,充分利用了基函数的正交性,使得采用较少的计算量就可以有效地计算单元刚度和质量矩阵,并且保证了高精度。

如果求解区域采用的网格剖分与问题给定的交界面相吻合,使得真解具有奇性的区域落在网格单元之间的边界处,由于谱元法本身的逼近方式在单元边界处的连续性仅为C0,当真解在交界面处其导数出现跳跃时,而离散格式恰好允许这样的非光滑性,因此采用谱元法求解这类交界面问题可以得到有效的数值结果。基于上述想法,本文的主要工作是通过一系列具有精确解的数值算例,采用模态基函数形式下的谱元法进行求解交界面问题的数值实验。对于二维问题,考虑了四边形单元和三角单元2种谱元法。选取的算例中既涉及具有间断系数的方程又涉及右端带有奇性源项的方程。通过数值实验发现,对于一维问题,可以得到具有指数阶收敛精度的数值解,对于二维问题也得到了较为满意的数值结果。

1 谱元法离散格式

1.1 一维问题

首先,考虑如下一维交界面边值问题

式中:r为常数;β为分片常数。当x∈Ω+时,β=β+;当x∈Ω-时,β=β-。

对求解区域Ω进行网格剖分T,记Ωe为网格

Ωe上进行如下积分:

将单元Ωe变换至标准单元Ωst=[-1,1],那么可以将上式中每个单元Ωe上涉及的积分转化为在Ωst上进行计算。假设在Ωst上,真解具有如下的N阶多项式展开逼近:

其中:φk(ξ)=Lk(ξ)-Lk+2(ξ);Lk(ξ) 为 Legendre多项式。

采用高斯积分公式进行数值积分,最后得到展开系数满足的如下线性代数方程组

其中:M为由单元刚度和质量矩阵装配后得到总体刚度和质量矩阵构成的系数矩阵,u为展开系数向量,u=,k=0,1,···,N,e=1,2,···,Nel;F为由右端项fe(x)确定的已知向量。

1.2 四边形单元(QSEM)

对于二维问题,首先考虑在矩形求解区域上采用四边形单元进行网格剖分,即:Ω =算,与一维问题相同,引入标准单元Ωst=[-1,1]2,从而使得在离散过程中每个单元Ωe上所涉及的微分和积分计算均可以在标准单元Ωst上一致进行。

假设在Ωst上,真解具有N阶多项式展开:数。采用四边形单元网格剖分的一大优点在于,二维模态基函数可以由一维基函数进行张量积得到,ψi,j(ξ,η)= ψi(ξ)ψj(η),即[3]:

充分利用Legendre多项式的正交性,采用上述基函数建立的单元Laplacian算子矩阵和质量矩阵具有如图1所示的稀疏结构。

图1 QSEM离散得到的单元Laplacian算子矩阵和质量矩阵的稀疏结构,多项式阶数N=9Fig.1 Sparse structure of the elemental Laplacian and mass matrices of QSEM with the modal bases of order N=9

1.3 三角单元(TSEM)

假设任意三角单元Ωe的3个顶点坐标为:{(xA,yA),(xB,yB),(xC,yC)},单元Ωe上的积分运算都可以通过如下坐标变换转化至参考三角单元τ={(ξ1,ξ2)|-1 ≤ξ1,ξ2;ξ1+ξ2≤ 0}上进行:

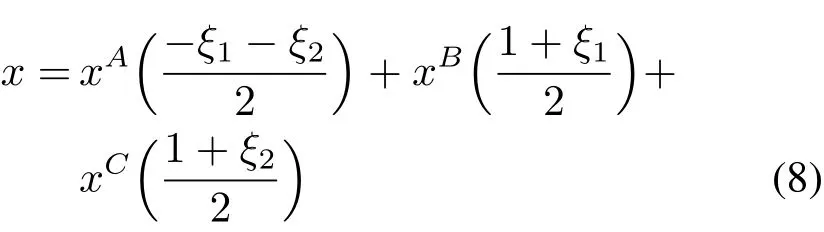
为了进一步计算方便,引入如下Duffy变换[8]及其逆变换

首先,通过式(8)、(9)将任意三角单元Ωe变换至参考三角单元τ,再借助Duffy变换,将参考三角单元τ变化至标准单元Ωst上,进行数值积分等相关计算(见图2)。

图2 任意三角单元(a)变换至参考三角单元τ(b),再变换至标准单元Ωst(c)进行数值积分Fig.2 Each triangular element(a)is mapped into the reference triangular τ;(b)then mapped into the standard elementΩst;(c)f i nally all local operations are evaluated in Ωst

根据图2(b)标记的参考三角单元τ的顶点顺序,给出如下三角单元的模态基函数[3]:

需要指出的是,Duffy变换是将标准单元Ωst的1条边压缩至三角形的1个顶点。如图2所示,边CC′通过变换后压缩至顶点C,顶点C′退化,使得数值积分时在η2方向上采用的GLL积分节点在顶点C处过于密集。如果在η1方向上采用GLL积分节点,而在η2方向上采用Gauss-Radau积分节点,那么顶点退化的问题不会对数值积分引入奇性。

最后,图3给出了单元Laplacian算子矩阵和质量矩阵的稀疏结构。

2 数值实验

选取一系列带有间断系数或奇性源项的交界面问题,采用模态基形式下的谱元法来进行数值离散求解,通过计算结果来验证谱元法求解这类问题的可行性和高效性。所有运算均借助Matlab 7数学软件得以实现,计算过程中所涉及的三角单元网格由Matlab自带的PDE工具箱生成。

算例1 首先,考虑如下一维交界面问题,方程具有间断系数且右端项含有奇性源Dirac函数[2]

精确解为

取µ=10,-10进行数值实验。表1和表2列出了L2误差随着选取不同的多项式展开阶数N和子区域个数Nel时的变化趋势,并且与文献[2]中采用的最小二乘Legendre谱配点法(LCM)得到的数值结果进行对比。从表中数据可以发现,对该一维交界面问题,当采用较少的未知量个数时,SEM得到了更高的精度,同时实现了指数阶收敛速度。图4和图5分别呈现了µ=10,-10时,得到的数值解和节点上的误差,这里取Nel=2,N=10。

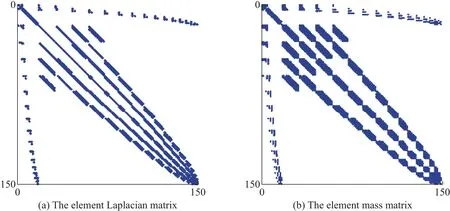
图3 TSEM离散得到的单元Laplacian算子矩阵和质量矩阵的稀疏结构,多项式阶数N=14Fig.3 Sparse structure of the elemental Laplacian and mass matrices of TSEM with the modal bases of order N=14

表1 LCM和SEM离散得到的L2误差对比,µ=10,算例1Tab.1 Comparison of the L2norm errors for LCM and SEM withµ=10,Example 1

表2 LCM和SEM离散得到的L2误差对比,µ=-10,算例1Tab.2 Comparison of the L2norm errors for LCM and SEM withµ=-10,Example 1

图4 SEM计算得到的数值解和节点误差,µ=10,Nel=2,N=10,算例1Fig.4 The numerical solution and pointwise errors of SEM withµ=10,Nel=2,N=10,Example 1

图5 SEM计算得到的数值解和节点误差,µ=-10,Nel=2,N=10算例1Fig.5 The numerical solution and pointwise errors of SEM withµ=-10,Nel=2,N=10,Example 1

算例2 考虑如下定义在Ω=(0,L)×(0,1)上的二维交界面问题[2]

精确解为:

其中:β-、β+、γ-、γ+、α、L、Ci的值与算例1中相同。

取µ=10进行数值测试,将求解区域Ω剖分为2 个子区域 [0,α]×[0,1],[α,L]×[0,1],采用 QSEM进行数值离散。在表3中,将其求解得到的L∞和L2误差与LCM[2]进行了对比。由于LCM的微分矩阵条件数随着配点个数的增加而增长得非常迅速,使得精度严重受到舍入误差的影响,而本文采用的QSEM可以达到计算机的容忍精度。

表3 LCM[2]和SEM离散得到的L∞和L2误差对比,µ=10,算例2Tab.3 Comparison of the L∞and L2norm errors for LCM and SEM withµ=10,Example 2

算例3 考虑如下二维交界面问题[9],采用TSEM进行数值求解

其中:交界面为曲线Γ=Ω-∩Ω+,Ω-=此外,[∇u·n]=∇u-·n-+∇u+·n+,n±为Ω±的单位外法向量。

精确解为:

其中:α=3,r0=1/2,R=1/2。f,µ和g可以由精确解代入方程推导得到。

间断系数β选取如下4组值进行数值测试:(1)β+=103,β-=1;(2)β+=106,β-=1;(3)β+=1,β-=103;(4)β+=1,β-=106。该算例的求解困难之处在于β+/β-的取值非常小或非常大。表4列出了当多项式展开阶数取为N=4,对应不同大小的三角单元网格剖分,TSEM数值计算得到的L∞和L2误差,其中h记为所有三角形单元的直径最大值。从表中数据可以发现,对于上述给出的4种间断系数选取,无论β+/β-的值非常大还是非常小,TSEM均得到了具有相同数量级的精度,对参数的选取并不敏感。图6展示了β+/β-=10-6,106时的数值解。

算例4 最后,考虑如下定义在Ω=[-1,1]2上,同时具有间断变系数以及右端奇性源项的问题[10]

表4 TSEM离散得到的L∞和L2误差,算例3Tab.4 The L∞and L2errors of TSEM,Example 3

图6 β+/β-取值非常小和非常大时,TSEM计算得到的数值解,算例3Fig.6 The numerical solutions of TSEM with the very small and big ratio β+/β-,Example 3

式中,f(x,y)=8r2+4并且

精确解为:及其满足的Dirichlet边界条件。

表5列出了b=10,C=0.1和b=-3,C=0.1时,采用TSEM计算得到的L∞和L2误差,图7所示为对应2组参数取值的数值解。

数值结果表明,采用TSEM求解同时具有间断变系数和奇性源项的交界面问题是可行有效的,得到了不错的数值结果。需要指出的是对于第二组参数值,由于b=-3＜0,问题本身并不是典型的椭圆方程,给求解带来一定的难度,然而还是得到了有效的计算精度。

表5 TSEM离散得到的L∞和L2误差,算例4Tab.5 The L∞and L2errors of TSEM,Example 4

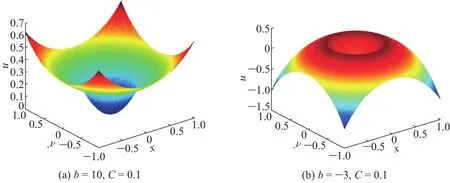
图7 TSEM计算得到的数值解,算例4Fig.7 The numerical solutions of TSEM,Example 4

3 结 语

本文对采用模态基函数形式下的谱元法求解交界面问题进行了数值实验。对于二维问题的网格剖分,不仅考虑了四边形单元还考虑了三角单元。选取一系列具有间断系数和右端带有奇性源项的交界面问题来验证谱元法的计算效果。数值结果表明,谱元法对于交界面问题的求解是可行并且有效的,对于一维问题实现指数阶收敛精度,对于二维问题也得到了较为理想的计算精度。

[1] WU Y,TRUSCOTT S,OKADA M.A f i nite difference scheme for an interface problem[J].Japan J Indust Appl Math,2010,27(2):239-262.

[2] SHIN B C,JUNG J H.Spectral collocation and radial basis function methods for one-dimensional interface problems[J].Appl Numer Math,2011,61(8):911-928.

[3] SHEN J,TANG T.Spectral and high-order methods with applications[M].2nd ed.Beijing:Science Press,2006.

[4] KARNIADAKIS G,SHERWIN S.Spectral/hp element methods for CFD[M].2nd ed.New York:Oxford University Press,2013.

[5] DEHGHAN M,SABOURI M.A spectral element method for solving the Pennesbioheat transfer equation by using triangular and quadrilateral elements[J].Appl Math Model,2012,36(12):6031-6049.

[6] FAKHAR–IZADI F,DEHGHAN M.A spectral element method using the modal basis and its application in solving second-order nonlinear partial differential equations[J].Math Method Appl Sci,2015,38(3):478-504.

[7] DUBINER M.Spectral methods on triangles and other domains[J].J Sci Comput,1991,6(4):345-390.

[8] DUFFY M G.Quadrature over a pyramid or cube of integrands with a singularity at a vertex[J].Siam Journal on Numerical Analysis,1982,19(6):1260-1262.

[9] HOU S,LIU X D.A numerical method for solving variable coeff i cient elliptic equation with interfaces[J].J Comput Phys,2005,202(2):411-445.

[10]LEVEQUE R J,LI Z.The immersed interface method for elliptic equations with discontinuous coeff i cients and singular sources[J].Siam J Numer Anal,1994,31(4),1019-1044.

A Numerical Study of The Modal Bases Spectral Element Method for Solving Interface Problems

SHAO Wenting(School of Science,Shanghai Polytechnic University,Shanghai 201209,China)

The numerical solution of one and two dimensional interface problems using the modal bases spectral element method(SEM)was studied.Equations with the discontinuous coeff i cient or singular source were concerned.For two dimensional cases,the implementations of the quadrilateral element(QSEM)and the triangular element(TSEM)were both investigated.Several numerical examples with exact solutions were provided to illustrate the feasibility and effectiveness of the modal bases SEM.Compared with other numerical results,exponential accuracy was regained for the one dimensional case,and better accuracy was also obtained for the two dimensional case.

spectral element method;quadrilateral elements;triangular elements;interface problems;discontinuous coeff i cient;singular source

O 241.82

A

1001-4543(2017)04-0283-08

10.19570/j.cnki.jsspu.2017.04.006

2017-04-27

邵文婷(1987–),女,上海人,讲师,博士,主要研究方向为偏微分方程数值解。E-mail:wtshao@sspu.edu.cn。

上海市自然科学基金项目(16ZR1412700),上海第二工业大学校重点学科建设项目(XXKZD1304)资助