一类具有年龄分布和加权总规模的周期种群系统的最优控制

沈荣涛，曹雪靓

(兰州交通大学 数理学院，甘肃 兰州 730000)

一类具有年龄分布和加权总规模的周期种群系统的最优控制

沈荣涛，曹雪靓

(兰州交通大学 数理学院，甘肃 兰州 730000)

种群动力系统的最优控制问题是控制理论中的一个重要的研究领域，它对种群的发展和控制提供了非常重要的参考价值。考虑到加权总规模和周期对种群发展的影响，本文给出了一类带年龄结构和周期的种群系统数学模型，其生死率依赖于个体年龄和加权总规模，借助不动点原理确立了系统的适定性，应用极大化序列法证明了最优解的存在性，得到了最优解的必要性。

种群规模；最优控制；年龄结构；加权总量；周期解

由于生物种群生存在周期性的变化环境中，所以研究周期性变化的种群模型更加符合实际。不少学者研究了带有周期性的种群系统的最优控制问题，获得不少成功。文献[1]和文献[2]最早讲述了年龄种群系统的控制问题和稳定性分析；文献[3]讨论了具有年龄结构和移民的非线性种群动态的最优生育控制问题；文献[4]研究了三种年龄结构的捕食者-食饵系统的最优控制；文献[5]讨论了一类非线性种群系统的最优控制问题，文献[6]研究了一类周期种群系统的适定性及最优控制，该文证明了非线性种群系统周期解的存在唯一性。本文再次基础上讨论下列非线性具有加权项的周期种群系统的最优控制问题：

(1)

其中:Q=(0,A)*(0,)，固定常数A,T分别表示个体最高寿命和系统演变周期。状态变量p(a,t)表示t时刻年龄为a的个体数量，控制函数u(a,t)代表收获努力度，S(t)表示t时刻种群的加权总量，ω为权函数，β，μ表示出生率和死亡率，他们的结构意味着不同年龄的个体对种群演化有不同的影响。

本文假设：

关于x有二阶连续的偏导数，满足|μx|≤M1,|μxx|≤M1,μ(a,t,S(t))=μ(a,t+T,S(t+T))。(H3)对任意(a,t,x)∈Q×(0,+)，0≤β(a,t,x)≤M2,β关于x局部Lipschitz连续，β(·,·,x)是x的减函数,关于x有连续的二阶偏导数,满足|βx|≤M2,|βxx|≤M2,且β(a,t,S(t))=β(a,t+T,S(t+T))。 (H4)对任意(a,t)∈Q,0≤ω(a,t)≤M3,M1,M2,M3为常数。

所谓系统(1)的解是指函数p∈L(Q)，满足

不妨假设u≡0，其他情形同法处理。

1 解对控制变量的连续依赖性

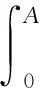
p(a,t,S)=b(t-a;S)∏(a,t,a;S),t≥A

。

(2)

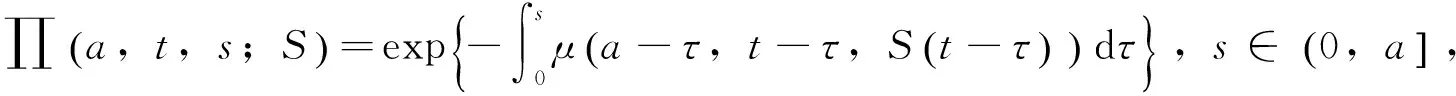
(3)

而b(·;S)为下列Volterra积分方程的T-周期解：

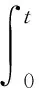
(4)

这里：

(5)

K(t,a,:S)=β(a,t,S(t))∏(a,t,a;S)。

(6)

(7)

|b(t;S)|≤M。

(8)

证明 由式(6)，得

由此得：|K(t,a;S1)-K(t,a;S2)|≤L1W(t)。

当A+T>t>A时，由式(4)得：

利用式(5)得 ：

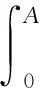
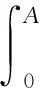
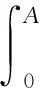
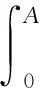
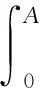
考虑到b的周期性，不妨设t∈[A,A+T]。根据Gronwall不等式，得：

2 最优性条件

其中q为下列共轭系统的解

(9)

证明：对∀v∈Tu(u*)(U在u*处的切锥)，当λ>0充分小时，u*+λv∈U，因此J(u*+λv)≥J(u*)，即:

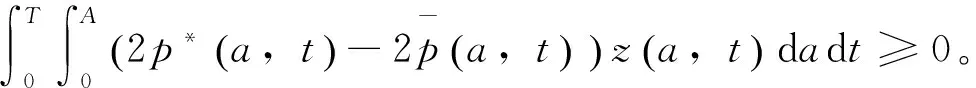
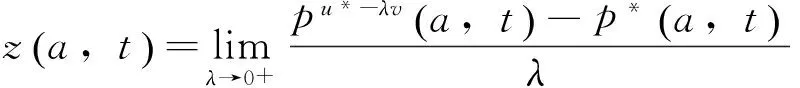
(10)

将式(10)的第一式乘以z(a,t)并在(0,A)×(0,T)上积分加上式(10)的第一式乘以q(a,t)在(0,A)×(0,T)上积分，得：

有文献[7]中定理3.2.5，即知定值的结论成立。

[1] Anita S.Analysis and control of age-dependent population dynamics[M].Dordrecht:Kluwer Academic Publishers,2000:31-104.

[2] Lotka A J.The stability of the normal age distribution[J].Proc Nat Acad Sci,1992,8:339-345.

[3] He Zerong, Wang Miansen.Optimal birth control problems for a nonlinear population dynamics with age-structure and immigration[J].应用数学,2003,16(4):136-142.

[4] Luo Zhixue, He Zerong, Li Wantong.Optimal birth control for predator-prey system of three species with age-structure[J].Applied Mathematics and Computation 2004,155:665-685.

[5] 何泽荣,朱广田.基于年龄分布和加权总规模的种群系统的最优收获控制[J].数学进展, 2006,35(3):316-324.

[6] 赵春,王绵森,何泽荣,等.一类周期种群系统的适定性及最有控制[J].应用数学,2004,17(4):551-556.

[7] 何泽荣.具有年龄结构的捕食种群系统的最优收获策略.系统科学和数学[J],2006,26(4):467-483.

[8] 赵春,王绵森,赵平.一类种群系统的适定性及最优收获问题[J].系统科学和数学,2005,25(1):1-12.

Optimal Control of Periodic Population System with Age Structure and Weighted Total Scale

SHEN Rongtao， CAO Xuejing

(Lanzhou Jiaotong University, Lanzhou 730070, China)

s: The optimal control problem of the population dynamics system is an important research field in the control theory, which provides a very important reference value for the development and the control of the population. Considering the effect of the weighted total scale and period on the population development, this paper presents a mathematical model of population system with age structure and period, which the mortality depends on the individual age and weighted total scale, then, the system is established by means of fixed point principle, finally, the existence of the optimal solution is proved by the maximal sequence method, and the necessity of the optimal solution is obtained.

population size; optimal control; age structure; weighted total; cycle

10.3969/j.issn.1674-5403.2017.04.020

O175.1

A

1674-5403(2017)04-0090-04

2017-09-19

沈荣涛(1992-)，男，江苏泰州人，在读硕士研究生，主要从事生物数学方面的研究.