修正的Peck公式在常州地铁隧道施工地表沉降预测中的应用

郭 二 新

(河南理工大学 土木工程学院，河南 焦作 454003)

修正的Peck公式在常州地铁隧道施工地表沉降预测中的应用

郭 二 新

(河南理工大学 土木工程学院，河南 焦作 454003)

本文以常州地铁项目部实测数据为依据，运用数学方法进行拟合，并结合实测数据对Peck公式进行修正，修正参数为地表最大沉降值和沉降槽宽度。得出了适应常州地区的Peck公式。结果表明：通过实测数据来分析得出地表最大沉降值修正范围在0.172 4～0.442 3，沉降槽的修正范围在0.556 4～0.746 1时，在运用Peck公式预测盾构施工引起的地表沉降时，和真实结果较为接近，且与原始Peck公式相比，预测结果更为可靠。

地铁隧道；地表沉降；Peck公式；修正系数

进入21世纪，伴随着社会的高速发展，现在城市都在大力修建地铁，而修建地铁采用的盾构法施工带来的地表沉降也是值得关注的问题[1]。目前，盾构法施工引起地面变形计算方法主要有经验公式法[2-3]、数值分析法[4]、解析法[5]、模型试验法[6]等。通过经验公式法来进行地表预测较为简单，其结果和工程实测数据基本相符，并且在大量的工程案例中得到了验证。但是，原始的Peck公式计算地表沉降有一定的误差，要进行参数的修正。当前，常州地铁正在全力建设，本文通过对常州地区地表沉降数据分析，对Peck公式进行修正，修正后的公式可为类似工程提供参考。

1 Peck公式的基本理论

Peck 公式是在大量的工程实测数据的基础上得到的，在此基础上并认为隧道施工中不考虑水的渗流，在隧道开挖之后的形成的沉降槽体积和盾构施工形成的地层损失体积一致。开挖形成的沉降槽曲线为正态分布曲线。横向槽如图1所示。Peck公式为：

图1 地表横向沉降槽示意图

(1)

(2)

式中:s(x)为距隧道中线x处的地表沉降值，m；v1为隧道工程单位长度地层损失，m3；i为地表沉降槽曲线拐点到隧道中心线的水平距离,m；smax为隧道中线处的最大地表沉降值,m。

由于地表测点沉降值与隧道轴线距离存在一一对应的关系，故将Peck公式进行线性回归[7]。

(3)

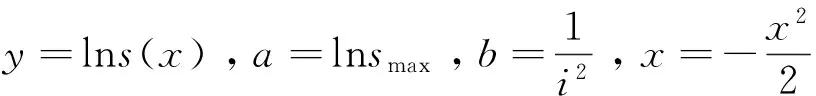
则式(3)可以简化为y=a+bx

由上式可以得到回归后的smax及i。

2 常州地铁隧道施工地表沉降预测分析

本文以江苏省常州市地铁为依托，其隧道采用土压平衡盾构机，盾构法区间衬砌管片外径6.2 m，内径5.5 m，隧道顶覆土深度为9.7 m～21.3 m。盾构穿越主要地层工程地质情况如表1所示。

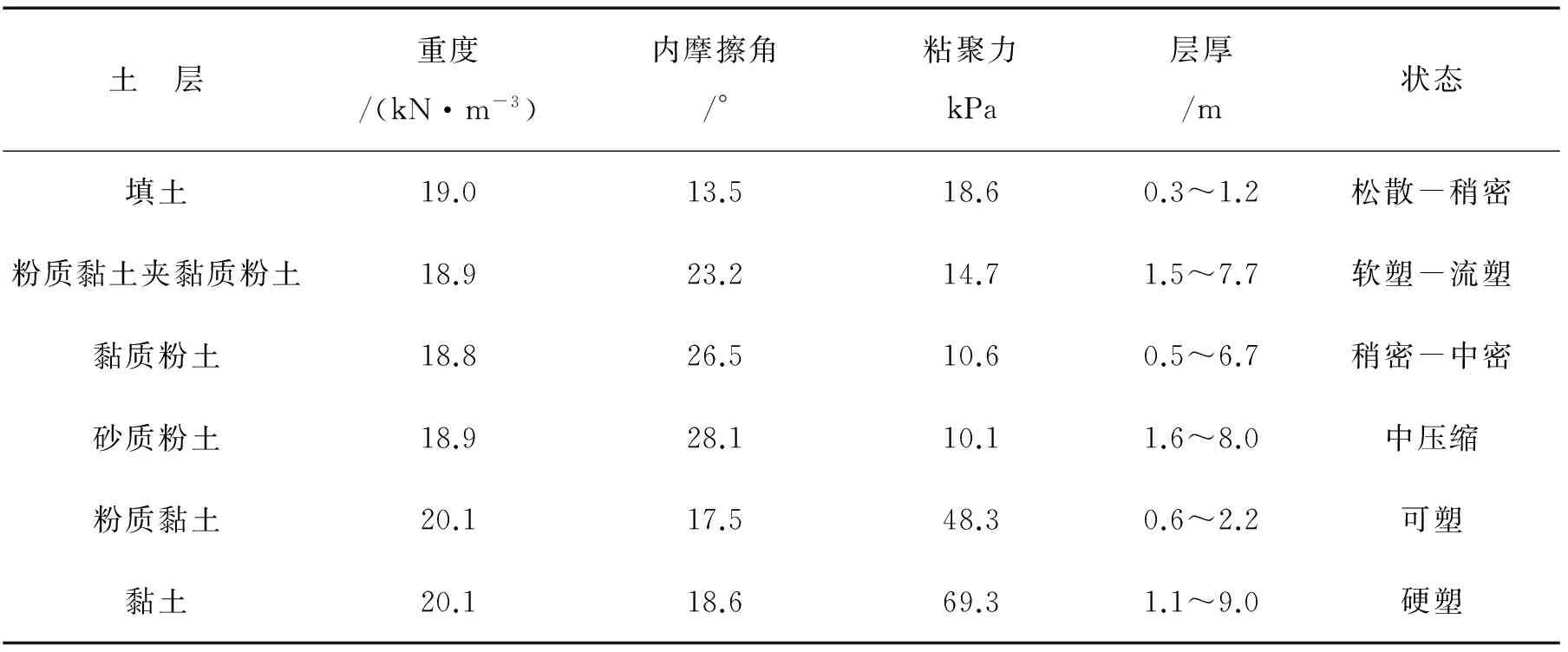
表1 工程地质参数

2.1 修正的Peck公式

本文根据在常州地铁获取的地表沉降数据，通过Peck公式拟合后，并将现场实测数据和拟合后的数据进行对比分析，通过分析得出适合本工程的地表预测沉降公式。

2.2 工程实测数据的获取

本文选取常州某标段科北～科南区间的典型断面，地面沉降监测点按照设计文件要求布设，横断面监测点每隔50 m布设一组，工程4个断面实测数据如表2所示。

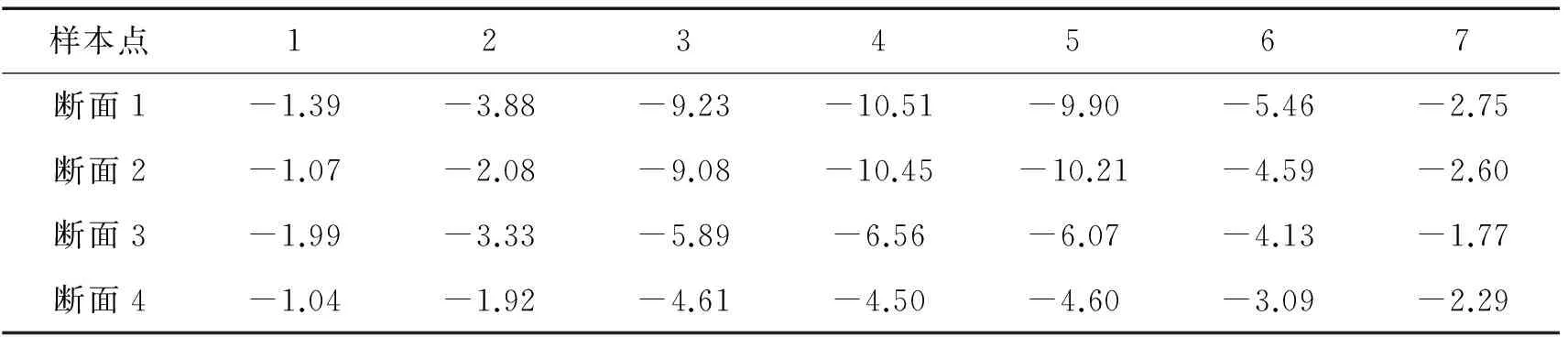
表2 沉降实测数据 /mm

2.3 原始的Peck预测曲线

通过查看断面地质资料，地层损失率[8]，根据文献结合本工程，取单位长度地层损失体积，则断面原始预测Peck数值如表3所示。

表3 预测Peck沉降值 /mm

从表3的预测值可以看出，原始的Peck预测值较大，不符合工程实际情况。

2.4 实测数据曲线和拟合后数据曲线对比

将实测数据和拟合后的数据进行对比，结果如表4～表7所示。

表4 断面1实测拟合数据对比 /mm

表5 断面2实测拟合数据对比 /mm

表6 断面3实测拟合数据对比 /mm

表7 断面4实测拟合数据对比 /mm

断面1数据经过回归后得到Smax=11.31 mm,沉降槽宽度i=6.565 m；断面2数据经过回归后得到Smax=9.48 mm，沉降槽宽度i=6.819 m；断面3数据经过回归后得到Smax=6.28 mm，沉降槽宽度i=8.367 m；断面4数据经过回归后得到Smax=4.40 mm，沉降槽宽度i=8.805 m。

通过对比表4～表7可以看出，拟合后曲线和实测数据曲线比较吻合，现对原始Peck公式增加两个修正系数，使其可以在常州盾构施工地表沉降预测中应用。修正后的Peck公式为:

(4)

式中：α为地表最大沉降修正系数；β为沉降槽宽度修正系数。

转换为线性函数后得到：

(5)

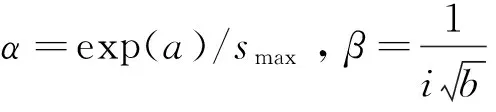
将计算出来的α、β作为Peck公式的修正系数，可以很好地预测断面沉降，较修正前的公式预测结果有了很大提高。

3 结 语

(1)根据Peck公式，计算了地表沉降的理论沉降值。

(2)根据地铁隧道开挖监测得到的数据，对Peck公式进行修正，地表最大沉降修正系数在0.172 4～0.442 3，沉降槽宽度系数在0.556 4～0.746 1，得到修正后的预测结果和实测结果更为接近。

(3)实测数据仅为地铁某标段，具有一定的局限性，但可以用类比的方法预测其它标段地表沉降，可以达到预期效果。

[1] 王梦恕.21世纪我国隧道及地下空间发展的探讨[J].铁道科学与工程学报，2004,1(1):7-8.

[2] 沈培良，张海波.上海地区地铁隧道盾构施工地面沉降分析[J].河海大学学报(自然科学版)2010,31(11):556-559.

[3] 周文波.盾构法隧道施工技术及应用[M].北京：中国建筑工业出版社，2004.

[4] 郑淑芬.盾构隧道施工地表沉降规律及控制措施[D].湖南：中南大学，2010.

[5] 黎春林，缪林昌.盾构隧道施工土体塑性区解析法研究[J].中国矿业大学学报，2014,03:402-408.

[6] 徐前卫.盾构施工参数的地层适应性模型试验及其理论研究[D].上海：同济大学，2006.

[7] 姚爱军，赵强，管江，等.基于北京地层地铁隧道施工的Peck公式的改进[J].地下空间与工程学报，2010,6(4)：789-73.

[8] 王建秀，邹宝平，付慧仙，等.盾构地层损失与对应地面沉降计算的对比分析[J].铁道工程学报，2013(9)：72-77.

Application of Modified Peck formula to Prediction of Ground Settlement in Changzhou Metro Tunnel Construction

GUO Erxin

(Henan Polytechnic University, Jiaozuo 454003, China)

In this paper, based on the measured data of Changzhou metro project, mathematical method is used to fit and combines the measured data to revise the Peck formula. The correction parameters are the maximum settlement of the ground surface and the width of the settlement trough. The Peck formula, which is adapted to Changzhou area, is obtained. The results showed that the use of Peck formula to predict the surface settlement caused by shield construction. The actual data analysis shows that the maximum surface settlement correction in the range of 0.172 4～0.442 3, settling tank correction in the range of 0.556 4～0.746 1. Real results and the original Peck formula are compared. And prediction results is more reliable.

subway tunnel；surface subsidence；Peck formula；correction coefficient

10.3969/j.issn.1674-5403.2017.04.009

TU93

A

1674-5403(2017)04-0037-04

2017-08-27

郭二新(1991-)，男，河南焦作人，在读硕士研究生，主要从事岩土地下方面的研究.