基于Holt-Winters与最小二乘支持向量机的混合预测模型

刘宝成，张仲荣，盛秀梅，程丽娟

(兰州交通大学 数理学院，甘肃 兰州 730070)

基于Holt-Winters与最小二乘支持向量机的混合预测模型

刘宝成，张仲荣，盛秀梅，程丽娟

(兰州交通大学 数理学院，甘肃 兰州 730070)

为了提高地下水埋深时间序列的预测精度，本文应用Holt-Winters三参数指数平滑法作为预测模型，使用最小二乘支持向量机对残差序列进行预测。由于核参数和惩罚因子在很大程度上直接影响了最小二乘支持向量机的预测性能，本文选用果蝇优化算法对其参数进行优化选取，该方法不仅能够建立最优的混合预测模型，而且能够很好地捕获地下水埋深序列的非线性特征。选用甘肃民勤县大坝乡城西八社地下水监测站点的数据来验证所建模型的预测性能，实验结果表明与传统的单一预测方法相比，本文所建混合预测模型提高了预测精度。

Holt-Winters三参数指数平滑；最小二乘支持向量机；果蝇优化算法；混合预测模型

地下水通常具有高质量、不需要化学处理可以直接用于人类社会活动的特点[1]，作为自然界重要的优质水资源，特别在干旱或半干旱地区地下水已成为人们主要的甚至唯一的供水水源[2]。地下水埋深是指潜水面至地表面的距离，是衡量地下水水量重要的标准，准确预测地下水埋深以减少有害影响并维持供需之间的差距对于水管理者和工程师来说是必要的[3]。目前时间序列预测方法，比如ARIMA、GM(1,1)、Holt-Winters指数平滑法以及回归模型已被广泛地应用地下水埋深[4-6]；地下水埋深由于诸多自然因素以及人类活动的影响，呈现出复杂的非线性特征[7]。传统的预测模型由于自身非线性逼近能力的不足，难以提高预测精度，基于神经网络(ANN)与机器学习有很强捕获非线性特征的能力，许多研究者已将其应用于地下水埋深预测，比如最小二乘支持向量机(LSSVM)[7]、GM(1,1)与ANN结合[8]、ANN与自适应模糊系统(ANFIS)结合[9]等取得了很好的预测结果；为了降低序列噪声的影响，小波降噪结合其他方法，比如小波-支持向量回归(WSVR)、小波-神经网络(WANN)[10-11]等,但是这些方法不能很好地拟合序列的季节性[12]。

本文结合Holt-Winters三参数指数平滑、最小二乘支持向量机(Least Squares Support Vector Machines, LSSVM)和果蝇优化算法(fruit fly optimization algorithm, FOA)建立混合预测模型Holt-Winters-FOA-LSSVM。首先，应用Holt-Winters三参数指数平滑对原序列拟合并预测，获得残差序列以及预测值；其次，应用LSSVM对残差序列进行预测，并使用FOA对LSSVM的两个参数进行优化，建立最优的混合预测模型；最后，通过实验与传统单一预测方法比较，来证明本文所建模型的有效性。

1 使用方法

1.1 Holt-Winters三参数指数平滑

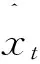
(1)

，

(2)

(3)

如采用乘法模型，构造如下：

(4)

(5)

(6)

1.2 最小二乘支持向量机

LSSVM是支持向量机的一种类型，是一种新型的人工智能技术[14]。最小二乘法支持向量机(LSSVM)模型被广泛地用于科学工程，LSSVM模型的优点，在有关的定量和定性方面，有很强的非线性拟合能力。

假设{(xi,yi)}为训练样本集，输入变量的值是i=1,2,…,N,xi∈Rn、yi∈Rn是输出变量，线性回归函数可用表示为：

f(x)=ωTφ(x)+b。

(7)

其中：x是输入向量，ω是权重矩阵，b是常数；根据结构最小化原则，优化问题就会转化为寻找函数f(x)，使达到最小：

(8)

其中：γ是惩罚因子，ei是误差；约束方程表示如下：

yi=ωTφ(xi)+b+ei,i=1,2,…,N。

(9)

引进拉格朗日乘子ai，得到：

(10)

根据KKT条件，LSSVM对方程(10)两边求偏导数，得到方程：

(11)

(12)

其中：y=[y1,y2,…,yN]T，a=[a1,a2,…,aN]T，lv=[1,1,…,1]T，I是单位矩阵，K是邻接矩阵，K(xi,xj)=φ(xi,xj)Tφ(xi)是满足Mercer理论的核矩阵。径向基函数具有广泛的收敛性和较强的泛化能力，是一种理想的回归核函数。公式(13)为径向基函数 所示：

(13)

其中：σ是核的宽度参数，它决定了样本数据分布的复杂性。它影响了LSSVM在特征空间中的超平面获得最佳分类的概括能力。调节惩罚因子γ和核参数σ是两个影响LSSVM基于径向核函数模型回归性能的超参数。a和b可通过最小二乘方法获得，则LSSVM的线性回归预测模型表达式：

(14)

调节惩罚因子γ和核参数σ的选取对LSSVM有很大的影响。为了获取最优参数得到最优模型以及考虑到算法的复杂性，本文采用果蝇优化算法(FOA)选取一组最优参数。

1.3 果蝇优化算法

台湾潘文超教授基于果蝇觅食行为，提出了一种新的全局优化的方法，称之为果蝇优化算法(FOA)，它的基本原理是粒子群优化算法[15-16]。作为一种比较全新的全局优化算法，果蝇优化算法不仅在科学和工程领域得到了广泛的应用，而且通过与其他方法进行混合运用到了数据挖掘中[17]。FOA算法的优点在于运算速度快，算法简单，并且对计算机的要求也比较低。根据上一节内容惩罚因子γ和核参数σ的选取直接影响LSSVM的拟合性能，因此，本文选用了果蝇优化算法优化参数，来建立最佳的LSSVM拟合模型。

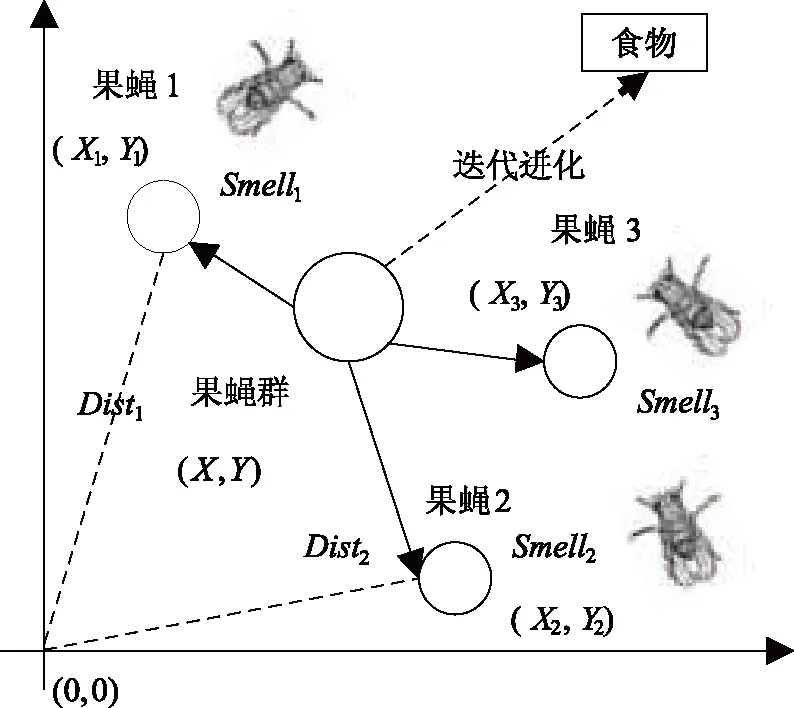
图1 果蝇组迭代搜索食物示意图

果蝇组迭代搜索食物示意图如图1所示。具体步骤如下：

(1) 果蝇群组的规模为Sizepop，迭代的最大数量为Maxgen，随机初始化果蝇群体位置为X-axis、Y-axis；

(2) 果蝇群体位置更新由公式(15)计算，其中随机值就是搜索到的距离：

(15)

(3) 计算果蝇与食物的距离Disti，然后再计算食物味道浓度判定值Si，Si值是距离的倒数。

(16)

(17)

味道浓度值Smelli如下：

Smelli=Function(Si)。

(18)

(4) 把味道浓度判定值Si代入味道浓度判定函数，计算出果蝇个体位置的味道浓度[15]；

(5) 找出此果蝇群体中味道浓度最佳的果蝇[16]：

[bestSmellbestindex]=min(Smelli)。

(19)

(6) 记录并保留最佳味道浓度值与x,y坐标[15-16]。此时果蝇群体利用视觉不断向目标位置靠近；

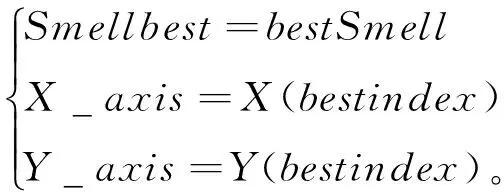
(20)

(7)重复执行步骤(3)～步骤(6)迭代寻优，当味道浓度不再优于先前迭代的味道浓度或迭代数量达到最大值时终止计算。

2 混合预测模型Holt-Winters-FOA-LSSVM建立

步骤1:根据原时间序列来确定Holt-Winters三参数指数平滑法的3个参数α、β、γ；建立Holt-Winters模拟预测模型，获得拟合值与预测值；

步骤2:结合FOA与LSSVM应用残差序列建立最优的残差预测模型；

步骤3:设置FOA的最大迭代次数、种群个数、果蝇随机位置及方向和LSSVM两个参数取值范围；

步骤4:使用真实值与LSSVM预测值的平均绝对百分比误差(MAPE)作为适应度函数，其中果蝇优化算法搜索达到最大迭代次数，最小的MAPE所对应的食物味道浓度判定值，及得到最优的一组参数；

步骤5:带入LSSVM建立最优的混合预测模型Holt-Winters-FOA-LSSVM。

3 应用实例

3.1 研究区及数据

本实验数据是甘肃省民勤县大坝乡城西八社(东经103°00′12″、北纬38°38′11″)从1999年1月至2013年12月(共180个数据)地下水监测站点数据，并由民勤县水务局提供。民勤县位于河西走廊东部石羊河下游，除西南一角与金昌、凉州区相接外，其余均被腾格里和巴丹吉林沙漠包围，是一个半封闭的内陆荒漠区，在阻碍两大沙漠汇合中起着极其重要的作用，是我国典型的资源型缺水地区[18]。

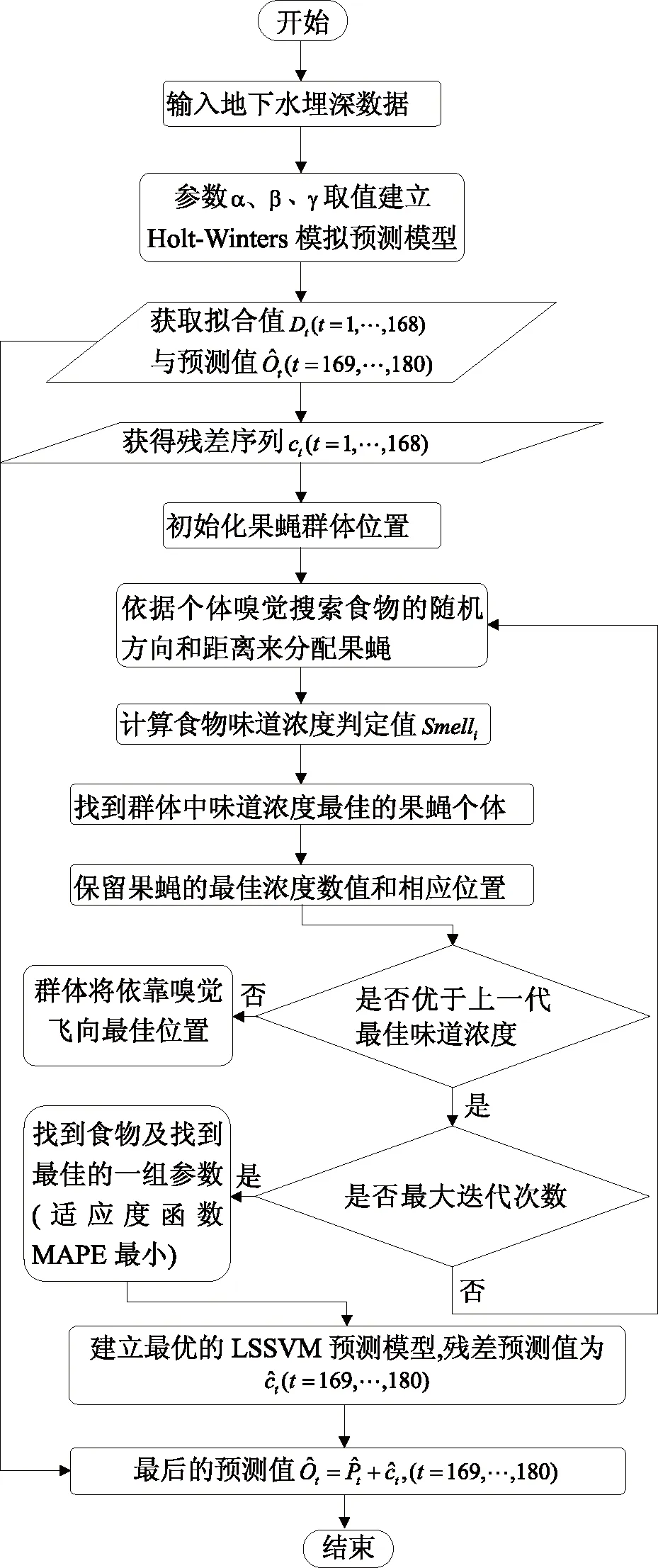
图2 Holt-Winters-FOA-LSSVM实验流程图

3.2 实验过程

Holt-Winters-FOA-LSSVM实验流程如图2所示。

步骤1：将原序列1991年1月至2012年12月数据(前168个数据)作为训练集，2013年12个月的数据(第169至180个数据)作为验证集。如图3原观测序列有明显的趋势与季节性，通过SAS模块可直接建立Holt-Winters 3参数指数平滑预测模型，由于随着时间的推移季节波动振幅随着序列水平的变化而变化，故采用乘法模型[13]，其中α、β取SAS默认的值0.106，通过多次试验γ值取0.5时拟合优度R2=0.971，所建立模型拟合效果如图4所示。

步骤3：设置FOA的最大迭代次数Maxgen=100、种群规模Sizepop=10、果蝇随机位置[-10,10]及方向[-1,1]和LSSVM两个参数γ范围设为[0,400]和σ初始范围为[0,10]；以残差序列ct(t=1,…,168)为训练集，经由FOA的50次迭代动态调整LSSVM参数后MAPE收敛情形；图5所示当迭代26次时适应度函数值MAPE达到最小，对应最优参数为γ=374.228和σ=1.358；

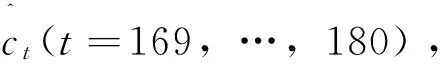
3.3 实验结果

通过与Holt-Winters、LSSVM和SARIMA预测模型相比较，由表1表明，本文所建模型预测结果MAE=0.068，MAPE=0.077均小于其他几种单一预测模型，即预测精度相对较好，2013年12个月预测值对比如图6所示。

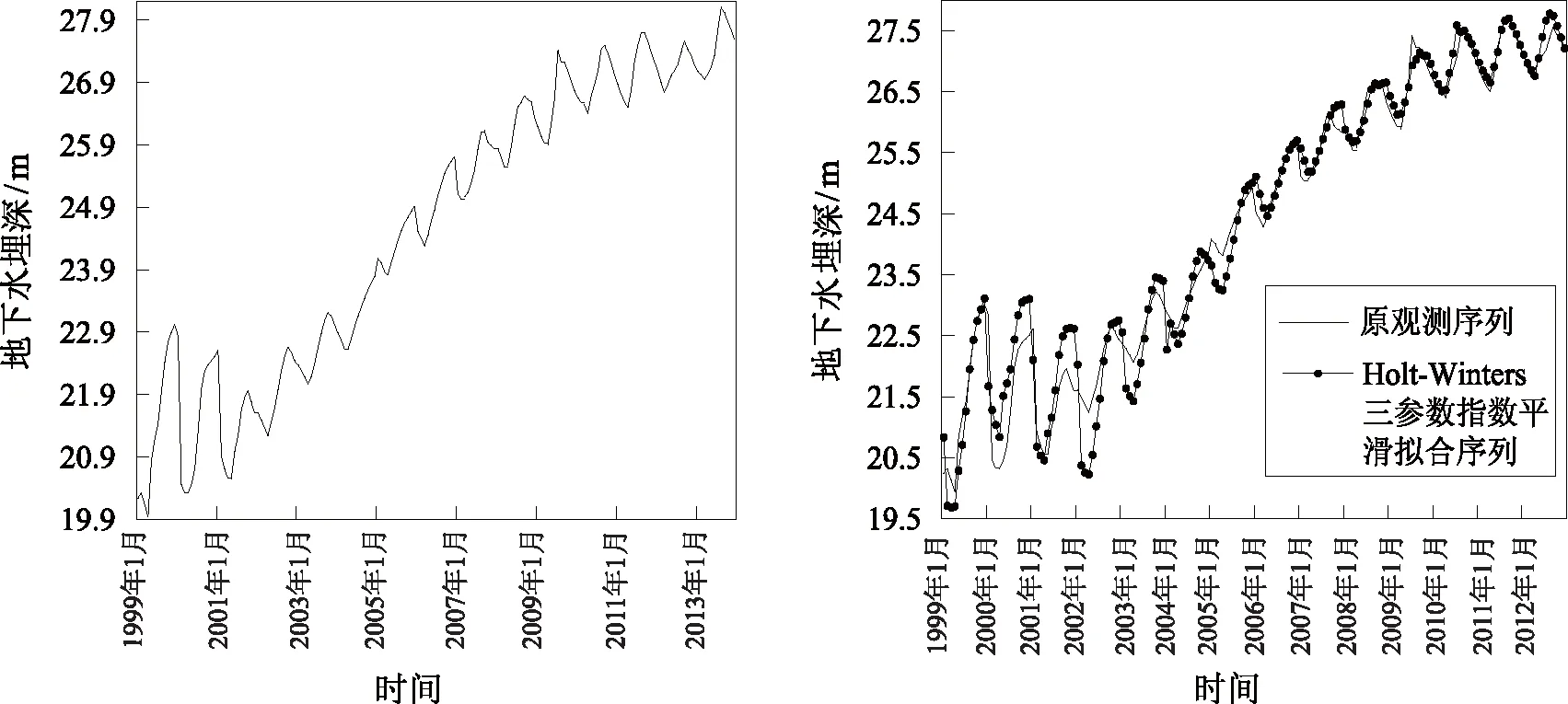
图3 原观测序列 图4 观测序列与拟合序列

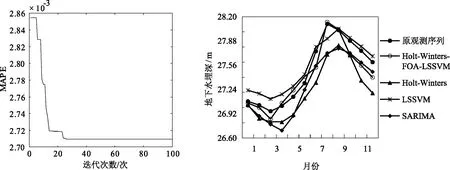
图5 迭代优化LSSVM参数后的MAPE收敛趋势图 图6 各模型预测结果对比图

模型Holt-Winters-FOA-LSSVMHolt-WintersLSSVMSARIMAMAE0.0680.1180.1230.097MAPE0.0770.0840.0970.121

4 结 语

本文基于建立混合预测模型的思路来提高地下水埋深预测精度。根据原序列的自身季节和趋势，用Holt-Winters三参数指数平滑法作为拟合预测模型来逼近其周期和趋势；为了很好地捕获序列的非线性特征，使用了LSSVM来拟合预测残差序列；考虑到调节因子γ和核参数σ直接影响着LSSVM的预测性能，选取了果蝇优化算法来搜索一组最优参数，建立一种最优的混合预测模型(Holt-Winters-FOA-LSSVM)。通过对甘肃民勤县大坝乡城西八社2013年地下水埋深数据预测结果表明，本文所建模型预测精度高于其他几种单一预测模型。本文不足之处为Holt-Winters参数使用了SAS软件默认值，为了能够获得更准确的预测需要进行优化选取。影响地下水埋深变化的因素有很多，为此，收集更多相关的数据，考虑影响地下水埋深多种因素，建立更精准的地下水埋深预测模型是即将开展的工作。

[1] Chitsazan M,Rahmani G,Neyamadpour A.Forecasting groundwater level by artificial neural networks as an alternative approach to groundwater modeling[J].Journal of the Geological Society of India,2015,85(1):98-106.

[2] 陆垂裕,孙青言,李慧,等.基于水循环模拟的干旱半干旱地区地下水补给评价[J].水利学报,2014,6(45):701-711.

[3] 闫浩文,刘艳平,曹建君.民勤绿洲地下水埋深影响因素分析及其变化趋势预测[J].中国水土保持科学,2013,11(2):45-51.

[4] 张云云,高子云,朱家明,等.组合预测模型在山东省地下水资源量预测中的应用[J].高师理科学刊,2016,36(6):24-28.

[5] 郝健,刘俊民.GM(1,1)模型改进技术在咸阳市地下水动态预测中的应用[J].水土保持研究,2011,18(3):252-256.

[6] 王美.Holt-Winters指数平滑法的地下水水位预测[J].青年时代,2016,4:161-162.

[7] 龙文,梁昔明,龙祖强,等.PSO-LSSVM灰色组合模型在地下水埋深预测中的应用[J].系统工程理论与实践,2013,33(1):243-248.

[8] Hadi E,Taher R.Simulation of groundwater level variations using wavelet combined with neural network,linear regression and support vector machine[J].Global and Planetary Change,2017(148):181-191.

[9] 杨婷,魏晓妹,胡国杰,等.灰色BP神经网络模型在民勤盆地地下水埋深动态预测中的应用[J].干旱地区农业研究,2011,29(3):204-208.

[10] Mamgholizadeh S,Moslemi K,Karami G.Prediction the Groundwater Level of Bastam Plain(Iran) by Artificial Neural Network(ANN) and Adaptive Neuro-Fuzzy Inference System (ANFIS)[J].Water Resources Management,2014,28(15):5433-5446.

[11] Suryanarayana C,Sudheer C,Mahammood V,et al.An integrated wavelet-support vector machine for groundwater level prediction in Visakhapatnam,India[J].Neurocomputing,2014,145(18):324-335.

[12] Guo Z H,Zhao J B,Zhang W Y,et al.A corrected hybrid approach for wind speed prediction in Hexi Corridor of China[J].Energy,2011,36:1668-1679.

[13] 王燕.应用时间序列分析[M].北京:中国人民大学出版社,2015:196-198.

[14] Gu Y P,Zhao W J,Wu Z S.Least squares support vector machine algorithm[J].Qinghua Daxue Xuebao/journal of Tsinghua University,2010,50(7):1063-1057.

[15] Wu X W,Li Q.Research of optimizing performance of fruit fly optimization algorithm and five kinds of intelligent algorithm [J].Fire Control & Command Control,2013,38(4):17-22.

[16] Pan W T,Pan W T.A new fruit fly optimization algorithm:taking the financial distress model as an example.Knowledge Based Systems[J].Knowledge-Based System,2012,26(2):69-74.

[17] Han J,Liu C.Fruit fly optimization algorithm based on bacterial chemotaxis[J].Journal of Computer Applications,2013,33(4):964-938.

[17] 肖笃宁,李小玉,宋冬梅,等.民勤绿洲地下水开采时空动态模拟[J].地球科学,2006,36(6):567-578.

Hybrid Prediction Model Based on Holt-Winters and Least Squares Support Vector Machine

LIU Baocheng, ZHANG Zhongrong, SHENG Xiumei, CHENG Lijuan

(Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to improve the prediction accuracy of the time series of groundwater depth, Holt-Winters three-parameter exponential smoothing method was used as the prediction model. The least squares support vector machine was also used to predict the residual sequence. As the prediction performance of least squares support vector machine, to a large extent, is directly affected by the kernel parameters and penalty factors, in this paper, the fruit fly optimization algorithm is used to optimize the parameters, which can not only establish the optimal hybrid forecasting model, but also can capture the Non-Linear characteristics and the predicted model was verified by the data collected from the groundwater monitoring station in the Minqin County Daba in Gansu Province. The experimental results show that the hybrid prediction model proposed in this paper improves the prediction accuracy compared with the traditional single prediction method.

Holt-Winters three-parameters exponential smoothing; least squares support vector machine; fruit fly optimization algorithm; hybrid prediction model

10.3969/j.issn.1674-5403.2017.04.018

O273.4

A

1674-5403(2017)04-0079-06

2017-06-16

刘宝成(1991-)，男，甘肃陇南人，在读硕士研究生，主要从事时空预测、机器学习、智能优化等方面的研究.

国家自然科学基金项目(41371435).