关于热传导方程源项系数的确定方法

甄苇苇，曾 剑，任建龙

(兰州交通大学 数理学院,甘肃 兰州 730070)

关于热传导方程源项系数的确定方法

甄苇苇，曾 剑，任建龙

(兰州交通大学 数理学院,甘肃 兰州 730070)

考虑了一类利用终端观测值反演热传导方程中源项系数的反问题,此类问题无论是在理论讨论还是在实际应用中都有极其重要的研究意义。基于最优控制框架下讨论了控制泛函极小元的存在性及其满足的必要条件,最后证明了最优解的唯一性及稳定性。

热传导方程;最优控制; 唯一性; 稳定性

本文考虑一类特殊的退化抛物型方程的源项系数的反问题,具体的数学模型如下:

(1)

其中0<α<1且c(x)和φ(x)是两个给定的光滑函数满足如下条件:

φ(x)∈L2(0,1),φ(x)≥0,φ(x)≡0,x∈(0,1),

(2)

而f(x)是未知系数满足:f∈L2(Q)。

假设给定如下的附加条件：

u(x,T)=g(x),x∈[0,l],

(3)

其中：g(x)是一个已知函数。利用条件(1)/条件(3)来同时确定函数u和f。

鉴于不适定问题的研究是偏微分方程的一个重要分支[1,2]。许多学者针对类似于式(1)/式(3)的问题求解做了大量的研究工作[3-8],该问题的难度在于问题的不适定。文献[3,4]中作者运用最优控制理论框架反演了方程ut-a(x)uxx+b(x)ux+c(x)u=f(x,t),(x,t)∈Q中的首项系数a(x),而对于反演方程中源项f=f(x)的情况可参见文献[5]。文献[6]利用观测数据从数值计算的角度对抛物型方程中未知源项的反演问题做了研究。文献[8]研究了一类时间分数阶扩散方程的源项反演问题。

1 最优化问题

由于问题是严重不适定的,故我们将原系数反演问题转化为如下的一个优化控制问题。

(4)

其中

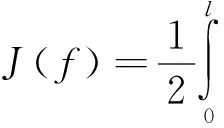
(5)

Α={f(x)|0<γ≤f≤κ,fx∈L2(0,1)},

(6)

u(x,t;f)是对应于任意给定的系数f(x)∈Α,方程(1)的解,N是正则化参数,γ,κ是两个给定的正数。

我们要求观测数据g(x)满足:

g(x)∈C(0,1),

(7)

并假设c(x)有下界,即c(x)≥c0,其中c0是一个正整数。

首先,我们对正问题做一些讨论,给出几个相关的定义及引理。

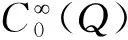
定义1.2u是方程(1)的弱解,如果满足u∈C([0,T];L2[0,1]∩B),u(x,0)=φ(x),x∈(0,1),并且对任意的t∈(0,T],有如下的积分方程:

(8)

引理1.1 对任意给定的f∈L(0,1),φ∈L(0,1),方程(1)存在唯一弱解且满足如下估计式：

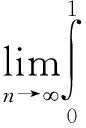
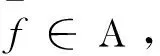
2 必要条件

定理2.1 令f是最优控制问题(5)的极小元,则存在三元函数组(u,v;f)满足下面条件：

(9)

(10)

和

(11)

证明: 对任意h∈Α,0≤δ≤1有

fδ≡(1-δ)f+δh∈Α。

则有

(12)

令uδ为方程(1)对应于给定系数f=fδ的解。由于f是控制问题(5)的最优解,从而有

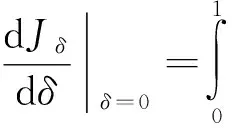
(13)

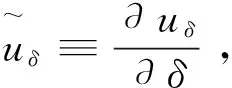
(14)

(15)

由式(14)得到

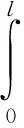
(16)

令Lξ=ξt-((x+τ)αξx)x+cξ,并假设η是下面方程的解

(17)

这里L*是算子L的共轭算子。

由格林公式可得

(18)

得

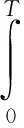
(19)

定理2.1证毕。

3 唯一性和稳定性

定理3.1 假设g1(x)和g2(x)是满足条件(7)的两个给定的函数,并令f1(x)和f2(x)为最优控制问题的p1为别对应于g1(x)和g2(x)的极小元。如果存在一点x0∈[0,1]使得f1(x0)=f2(x0),则有下面的估计

这里C与T,l及N无关。

证明: 在式(11)中,当f=f1时取h=f2,而当f=f2时取h=f1,于是有

(20)

(21)

这里{ui,ξi}(i=1,2)分别是方程(9)和方程(10)当f=fi(i=1,2)时的解。

令u1-u2=U,ξ1+ξ2=E,则U和E满足

(22)

(23)

由极值原理知方程(23)只有零解,于是可得

ξ1(x,t)=-ξ2(x,t)。

(24)

此外,ξ1满足下面的方程

(25)

由式(22)和式(25)可知

U(x,t)=-ξ1(x,t)。

(26)

由式(20)、式(21)、式(25)及式(26)可得

(27)

由定理3.1的假设和HÖlder不等式,在0≤x≤1上有

(28)

由此可得

(29)

合并式(28)和式(29)有

定理证毕。

[1] 姜礼尚,陈亚浙.数学物理方程讲义[M].3版.北京:高等教育出版社,2006:108-158.

[2] 刘继军.不适定问题的正则化方法及应用[M].北京:科学出版社,2005:51-55.

[3] Jiang L S,Chen Q H,Wang L J.A new well-posed algorithm to recover implied local volatility[J].Quantitative Finance,2003,3(6):451-457.

[4] Jiang L S,Tao Y S.Identifying the volatility of underlying assets from option prices[J].Inverse Problems,2001,17(1):137-155.

[5] Yang L,Deng Z C,Yu J N.Optimization method for the inverse problem of reconstructing the source term in a parabolic equation[J].Math Comput Simul,2009,80(2):314-326.

[6] Yang L,Dehghan M,Yu J N.Inverse probem of time-dependent heat sources numerical reconstruction[J].Math Comput Simul,2011,81(8):1656-1672.

[7] Deng Z C,Yang L.An inverse problem of identifying the radiative coefficient in a degenerate parabolic equation[J].Chinese Annals Math,2014,35B(3):355-382.

[8] Yang F, Fu C L.Amollification regularization method for the inverse spatial-dependent heat source problem[J].J Comput Appl Math,2014,255(2): 555-567.

Method for Identifying the Source Term Coefficient in a Class of Heat Conduction Equations

ZHEN Weiwei, ZENG Jian, REN Jianlong

(Lanzhou Jiaotong University, Lanzhou 730070, China)

This paper studies an inverse problem of identifying the source term coefficient in a class of heat conduction equations from the final observation, which is of great significance both in theory and practice. Based on the optimal control framework, the existence of the minimizer and the necessary conditions are deduced. At the end of the paper, the uniqueness and the stability of the solution are also proved.

heat conduction equations; optimal control; uniqueness; stability

10.3969/j.issn.1674-5403.2017.04.015

O175.26

A

1674-5403(2017)04-0065-05

2017-07-17

甄苇苇(1994-),女,山西长治人,在读硕士研究生,主要从事数学物理反问题方面的研究.

国家自然科学基金项目(11261029).