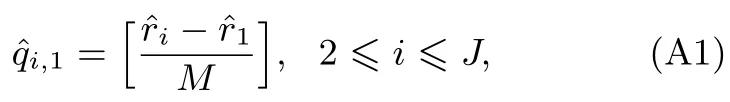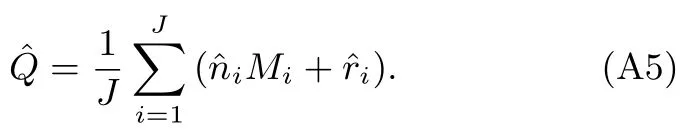单次空时域并行欠采样下的频率和到达角联合估计∗

黄翔东 刘明卓 杨琳 刘琨 刘铁根

1)(天津大学电气自动化与信息工程学院,天津 300072)

2)(天津大学精密仪器与光电子学院,天津 300072)

单次空时域并行欠采样下的频率和到达角联合估计∗

黄翔东1)刘明卓1)杨琳1)刘琨2)†刘铁根2)

1)(天津大学电气自动化与信息工程学院,天津 300072)

2)(天津大学精密仪器与光电子学院,天津 300072)

欠采样,到达角估计,频率估计,中国余数定理

1 引 言

在雷达[1]、无线通信系统[2,3]、电子战等被动目标感知领域[4,5],入射电磁波的波长和到达角(direction of arrival,DOA)是至关重要的两个待测物理量.然而,随着S波段(如美国宙斯盾防御系统)、C波段、X波段(如美军萨德反导系统)、K波段等高频段雷达应用在近年来逐渐展开,客观上要求在信号处理领域研发出相应的入射波长(实际上是频率的检测)和DOA的检测算法.然而以上高频段应用也给信号检测带来两个突出问题:一方面,由于Ngsuist采样定律要求采样速率大于等于检测信号最高频率的两倍,现有的模数转换器(analog to digital converter,ADC)完全达不到如此高的采样要求;另一方面,由于传统均匀阵列天线要求阵元间距小于等于信号最小波长的一半,故以上波段的雷达阵列天线的阵元布置相当困难(如X波段AN/TPY-2的雷达系统需在9.2 m2的小范围内密集安装30464个天线阵元),必然使得阵元间耦合变得非常严重.因此,急需研发出可在空间域和时间域均做稀疏欠采样下的低成本、低复杂度、低功耗的频率和DOA联合估计算法.

目前,频率与DOA的联合估计的解决方案绝大多数都基于传统特征空子空间分解法(如:多重信号分类(multiple signal classi fication,MUSIC)算法、借助旋转不变技术估计信号参数(estimating signal parameters via rotational invariance techniques,ESPRIT)算法或最大似然(maximum likelihood,ML)算法.文献[6]结合快速傅里叶变换(fast fourier transform,FFT)和ML算法实现空时域参数联合估计,但是该算法需要通过多次迭代进行多维度搜索,计算复杂度较高;文献[7—10]利用子空间算法来实现频率与DOA的联合估计,其中文献[7]提出了长基线和短基线的概念,在均匀线阵中不同位置的阵元上应用不同的采样速率,利用ESPRIT算法实现频率和DOA联合估计;文献[9]提出一种树形结构FSF(frequency-spacefrequency)-MUSIC算法,即先后多次利用MUSIC算法进行特征值分解与变换,从而实现频率与DOA的联合估计.但是以上算法都是基于传统均匀线阵和Nysuist采样定理,且只适合检测低于10 MHz的信号.

近年来,稀疏阵列因其有灵活的布置方案(如最小冗余阵列[11]、最小空洞阵列[12]和互素阵列[13−15]等)、更低的硬件成本和空间限制(有利于减小阵元间耦合),故吸引了越来越多的关注.但这些稀疏阵列中,最小冗余阵列和最小空洞阵列不具有闭合的推导形式,因而难以在实际工程中应用;而Vaidyanathan提出的互素阵列(coprime array)[13−15]及其改进后的版本[16]和稀疏嵌套阵列[17−19],在某些局部阵元区域,仍不是稀疏的.在设计DOA估计算法方面,通常需要将这些稀疏阵列的观测协方差矩阵转化为Nysuist空间采样的协方差矩阵,再对其做MUSIC分解而测算出入射方位角值.但这些估计器无法在欠采样率条件下估计入射信号的频率值(文献[11—19]均把入射频率当做已知量来处理),故仅是单参数估计器,而不是联合估计器.

文献[20]提出时空欠采样条件下的频率与DOA联合估计算法,但是该算法需要在单阵元上进行多次时域欠采样(各次采样都得到等长的快拍序列,采样次数与阵元数目相等),并借助离散傅里叶变换(discrete Fourier transform,DFT)和中国余数定理得到模糊频率估计,再利用多阵元的采样值的DFT相位差获得DOA估计值.很显然,该方法对单阵元做多次采样,不仅耗费了过多的延时,不利于捕获快速目标,而且会增大数据处理负担.本文提出单次空时欠采样下的基于互素稀疏阵列的频率与DOA联合估计算法,该算法基于一种具有高度稀疏度的阵列,把闭式鲁棒中国余数定理(closed-form Chinese remainder theorem,closedform CRT)[21]与Tsui谱校正器[22]结合起来,仅仅依据稀疏分布的阵元上做单次并行欠采样下的快拍数据,即可获得高精度的频率与DOA的联合估计,从而大大缩短了延时.仿真结果证明了本文所提出的联合估计算法的可行性,并展现出优良的性能.

2 互素稀疏阵列与信号模型

互素稀疏阵列结构如图1所示,由L(L>1)个传感器阵元组成非均匀稀疏阵列.令阵元间距dl具有如下形式:

其中,λ为允许的最高检测频率对应的波长(本文称之为单位波长),Mθ为正整数,而Γ1,Γ2,···,ΓL−1互为素数,显然,(1)和 (2)式可以保证dl≫λ/2,l=1,2,···,L−1,即阵列具有很高的空间稀疏度.

不失一般性,将图1的DOA为θ0的入射的远场目标的窄带信号表示如下:

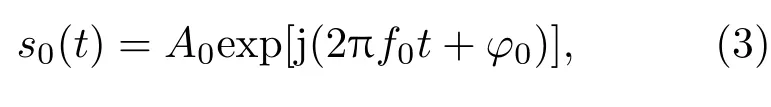
其中A0,f0,φ0分别表示信号的幅值、频率和初相.

图1稀疏阵列的每个阵元上都配置了两个采样速率分别为fs1,fs2的ADC采样器,对其做如下数值设置:

图1 互素稀疏阵列结构Fig.1.Structure of the proposed relaxed coprime sparse array.

其中η1和η2是互素整数,Mf是正整数.对Mf,η1,η2做适度设置,可以使得fs1,fs2≪f0,也就是说,任意阵元上得到的都是时间域高度欠采样的快拍数据.

联合估计器的任务,就是在上述空间域和时间域均为高度欠采样的苛刻条件下,仅仅依靠L阵元上单次并行欠采样的快拍数据(文献[20]需要在单阵元上做多次采样),高精度地估计出入射信号的频率值和DOA值.

3 频率估计算法

3.1 单目标频率估计模型

考虑噪声和相移的因素,不妨将第l个阵元上的接收信号表示为

其中φl表示信号到达阵元的相位,ξl(t)表示零均值高斯白噪声.将t=n/fs1,t=n/fs2代入(5)式,可得到两个长度为Mf的序列,

其中,n=0,1,···,Mf−1.

由于欠采样,(6)式中的f0/fs1和f0/fs2必然都大于1,从而有

联立(6)和(7)式,则xl,1(n)和xl,2(n)可进一步表示为

其中,n=0,···,Mf−1.

为方便表示,令

将(4)和(9)式代入(7)式中,有

(10)式完全符合文献[21]的闭式鲁棒中国余数定理模型为模值,为余数,n1,n2为折叠整数),关键在于两个归一化频率的估计.另外,为估计θ0,(8)式的相位值φl也需估计出来.

3.2 基于CRT和谱校正的单目标频率和相位估计

DFT是常用的频率和相位测量手段,然而由于固定的采样速率与未知的信号频率通常不成整数倍关系,无法直接从离散序列的DFT中获得准确的频率、幅值和相位估计值.故需要借助频谱校正措施获得这3个参数的估计.文献[22]提出的Tsui估计器,只需通过1次迭代操作即可获得高精度频率估计值(其频率估计误差方差接近克拉美-罗理论下限).故本文采用Tsui估计器进行频谱校正,其流程如图2所示.

结合3.1节的单目标模型和图2流程,可在各阵元上获得目标源的频率估计和到达相位估计,步骤如下.

图2 Tsui估计器流程图Fig.2.Overall data flow of the Tsui estimator.

步骤1在任意第l个阵元上(l=1,2,···,L),对欠采样序列xl,1(n),xl,2(n)均按照图2的Tsui谱校正流程进行参数估计,分别得到参数估计集

步骤2构造余数模值和重构通?道数J=2.将这些参数代入附录A所列出的闭式中国余数定理重构流程,得到第l个阵元上的频率估计结果

步骤3构造均值矢量取其相角作为第l个阵元的相位估计,即

步骤3的矢量平均操作,起到了抑制噪声干扰、提升φl估计精度的作用,为后续DOA估计打下基础.

3.3 最终信号频率估计

既然DOA是在估计入射频率f0后测出的,若f0的估计精度不足,其估计误差会蔓延到DOA估计中去.提高f0估计精度的解决办法是,对所获得的各阵元入射频率的粗估计值做平均,即

4 DOA估计

假设远场窄带信号s0(t)以角度θ0入射到图1所示的稀疏阵列天线上,则其第l个阵元和第l+1个阵元所接收到的相位差可以表示为

由于阵元间距dl≫λ/2,导致相位差必然包含2π整周模糊,即

其中nl表示未知整数,故mod 2π(mod表示模除操作).将(12)和(13)式整理合并,

将(1)式代入到(14)式,有

令

联立(15)和(16)式,有

显然,(17)式符合闭式鲁棒CRT模型,其中M1,···,ML−1表示模值,r1,···,rL−1表示余数,n1,···,nL−1表示折叠整数.把CRT的重构值和已得到的波长估计值代入(16)式,即可得DOA估计值

5 联合估计器的总流程及其性能分析

5.1 联合估计器总流程

基于前两节的阐述,可将空时欠采样下入射信号的频率和DOA联合估计器的流程总结如图3所示.

从图3可以看出,只需将L个稀疏阵元上并行采样得到的欠采样序列对{xl,1(n),xl,2(n),l=1,2,···,L}馈入联合估计器,经基于CRT和谱校正的频率、相位估计器(详见3.2节的三步骤)做并行处理后,对其输出的频率估计值做简单平均即可得到入射信号频率估计值对其输出的相位估计值ˆφ1,···,ˆφL做差分、2π模除、对应因子相乘和闭式鲁棒CRT重构、反三角运算处理后,即可得到DOA估计值

图3 空时欠采样下入射信号的频率和DOA联合估计流程图Fig.3.Overall data flow of the proposed frequency and DOA joint estimator.

5.2 联合估计器性能分析

入射信号频率测量精度和DOA估计的噪声鲁棒性这两方面性能是工程应用中所关心的.

入射信号的频率测量精度可由足够多的快拍数Mf和平均操作来保证.从图3可看出,对各阵元已经测出的入射频率估计结果做平均,可起到抑制噪声干扰,提升入射信号测量精度的作用.

而DOA估计的噪声鲁棒性是由CRT重构的余数误差容许上限决定的.文献[21]已证明:闭式鲁棒CRT的余数误差容许上限等于各模值最大公约数(greatest common divisor,gcd)的1/4,由于(16)式CRT模型中的模值为Ml=MθΓl,l=1,2,···,L−1,故其估计误差容许上限为gcd{M1,···,ML−1}/4=Mθ/4. 令设第l个阵元与第l+1个阵元的理论相位差为∆φl,相位差测量误差为εl,即有

则其CRT重构的余数误差应满足

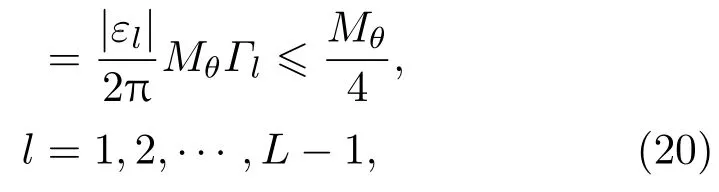
即相位差测量误差εl要求满足

(21)式表明: 素数组{Γ1,···,ΓL−1}值越大(对应阵元间距dl也越大),相位差测量误差的容错上限就越小.从而可得出结论:DOA估计的噪声鲁棒性与阵列的稀疏度成反比.

6 实 验

6.1 频率和DOA联合估计

将图1的阵列模型参数设置如下:θ0=38◦,假设检测X波段(即f∈[8,12]GHz,相应的阵列单位波长λ=c/fmax=0.025 m);本地阵列信噪比(signal-to-noise ratio,SNR)设为5 dB,阵元数L=3,Mθ=2,互素整数{Γ1,Γ2}={5,7}. 根据(1)和(2)式可算出阵元间距:{d1,d2}={0.175 m,0.125 m}. 显然,d1,d2≫λ/2,阵列具有很高的空间稀疏度.

对(3)式的目标源参数设置如下:f0=8 GHz(λ0=c/f0=0.0375 mm),A0=2,φ0=100◦;另外,互素数组{η1,η2}={5011,5021},快拍数Mf=1024.根据(4)式将两个ADC的采样速率设置为:fs1=Mfη1=5.131264 MHz,fs2=Mfη2=5.141504 MHz.显然,fs1,fs2≪f0,属于高度时域欠采样情况.

表1列出了本文提出的联合估计器测算的各阵元频率检测值、最终的频率估计值和DOA估计值等实验结果(文献[20]的联合估计器只能在多次欠采样条件下工作,故无法和在单次并行欠采样条件下工作的本文提出的联合估计器做对比).

表1 频率与DOA联合估计实验参数与结果Table 1.Parameters and results of the frequency and DOA joint estimation.

从表1可推出:频率估计的相对误差仅为|ˆf0−f0|/f0×100%=1.575×10−7%,而DOA测量误差仅为0.0602◦.

6.2 不同的时间域欠采样对频率估计的噪声鲁棒性的影响

时间域欠采样程度可通过改变互素整数η1,η2值来调整. 保留6.1节的仿真参数设置,考虑两种互素整数取值情况:{η1,η2}={5011,5021}和{η1,η2}={7013,7019}(即对应两组采样速率{fs1,fs2}={5.131264,5.141504}MHz和{fs1,fs2}={7.181312,7.187456}MHz);另外,设置信噪比测试区间为SNR∈[−25,5]dB,对每种SNR条件进行1000次蒙特卡罗测试,若某次测试的频率估计值ˆf0满足|ˆf0−f0|

如图4所示, 对于{η1,η2}={5011,5021}的情况,当SNR>−6 dB,频率检测成功率达到100%,而对于{η1,η2}={7013,7019}的情况,当SNR>−3 dB,频率检测成功率达到100%,即前

图4 频率检测成功概率Fig.4.Probability of frequency detection.

6.3 不同的空间域欠采样对DOA估计的噪声鲁棒性的影响

空间域欠采样程度(即阵列稀疏度)可通过改变互素组{Γ1,···,ΓL−1}值来调整. 在保留6.1节的主要仿真参数设置的基础上,仅考虑虑两组Γ取值:{Γ1,Γ2}={5,7}和{Γ1,Γ2}={13,17},根据(1)和(2)式可算出阵元间距:{d1,d2}={0.175 m,0.125 m},{d1,d2}={0.425 m,0.325 m}.设定SNR∈[−25,5]dB,对于每种SNR条件进行1000次蒙特卡罗测试,若某次测试的DOA测量值ˆθ0满足|ˆθ0−θ0|<1◦,则视为检测成功,否则视为失败.

如图5所示,对于{Γ1,Γ2}={5,7}的情况,当SNR>−6 dB时,DOA检测成功率达到100%.对于{Γ1,Γ2}={13,17}的情况,当SNR>0 dB,DOA检测成功率达到100%,即前者成功率曲线相比于后者左移了约6 dB,这就意味着当互素组{Γ1,···,ΓL−1}取值较小时(即阵元间距较小, 阵列稀疏度较低),DOA估计的抗噪鲁棒性更好.从而验证了5.2节得出的DOA估计的噪声鲁棒性与阵列的稀疏度成反比的结论.者的成功率曲线相比于后者约左移了3 dB.这就意味着当互素组{η1,η2}取值较小时,频率估计的噪声鲁棒性更好.其原因在于:互素组{η1,η2}取值越小,采样速率就越小,采样时间间隔就越大,当快拍数Mf固定时,必然占据更长的观测时间,故频率测量的噪声鲁棒性增强.

图5 DOA检测成功概率Fig.5.Probability of DOA detection.

6.4 与经典互素MUSIC分解的DOA估计器的性能比较

将本文提出的联合估计器的DOA测量结果与文献[16]提出的基于经典互素阵列的(包括两个子阵列)MUSIC估计器做对比,检测频段仍为f∈[8,12]GHz(对应单位波长λ=0.025 m).将(5)式信号模型中的参数共同设置为:入射信号频率f0=9 GHz,幅值A0=2,初相φ0=100◦;令θ0=45◦,且两个估计器的接收阵元个数同为L=6个,每个阵元收集的快拍数目同为Mf=512.需指出,文献[16]的估计器仅能测算DOA值,无法实现时域欠采样下的频率估计,因而本仿真只能把f0值当作已知量来处理.另外,为实现L=6个阵元布置,该估计器还需指定1对素数N=3,M=2,则其中第1个子阵的N=3个阵元的参考坐标为

第2个子阵的2M−1=3个阵元的参考坐标为

由于两个子阵排布在同一直线上,则所有6个阵元的参考坐标为故第2,3,4个阵元之间的距离仅为λ/2,在空间域不完全符合稀疏采样.

对于本文的联合估计器,设定(4)式中的两个素数为[η1,η2]=[5101,5107](对应两个ADC的采样速率为[fs1,fs2]=[2.611712,2.614784]MHz).另外,令Mθ=2,设定L−1=5个素数值为{Γ1,···,Γ5}=[2,3,5,7,11], 将其代入(1)式和(2)式,可确定所有6个阵元的参考坐标为从而所有相邻阵元的间距都远远大于λ/2,属于稀疏度非常高的空间采样.

考虑信噪比测试区间为SNR∈[−15,30]dB,对于每种SNR条件,对两个估计器均进行1000次蒙特卡罗测试,并统计其DOA测量值的均方根误差(root mean square error,RMSE),如图6所示.

图6 DOA估计的RMSE对比Fig.6.RMSE comparion of DOA estimation.

从图6的RMSE曲线,可得出如下两个结论.

1)当SNR高于6 dB时,本文估计器的DOA测量具有非常高的精度,其RMSE值比文献[16]的互素MUSIC估计器低3个数量级.这是因为本文估计器所选取的内嵌的频谱校正器精度非常高,且CRT本身不会引入重构误差,故DOA估计精度高;而文献[16]的估计器,需要将6个阵元上直接观测得到的协方差矩阵转化为Nysuist意义上的协方差矩阵,由于空间欠采样的缘故,会引入误差,降低了精度.

2)在低SNR区域,两个估计器都会出现阈值效应(即SNR低于该阈值时估计器失效),具体而言,文献[16]估计器的SNR阈值为−12 dB,本文估计器的SNR阈值为6 dB(即鲁棒性更差).这是因为,本文估计器的阵列阵元是高度稀疏放置的(如前所述,其最小阵元间距高达420×λ/2),而文献[16]的阵列阵元是局部稀疏放置的(如前所述,其最小阵元间距仅为λ/2),故根据5.2节得出的“DOA估计的噪声鲁棒性与阵列的稀疏度成反比”的结论,本文估计器的噪声鲁棒性不如文献[16]的估计器,这可看作是高度稀疏的空间采样所付出的代价.

7 结 论

本文提出了基于互素稀疏阵列的单目标入射频率和DOA联合估计器,该估计器融合了中国余数定理、阵列信号处理和频谱校正三大理论,使得空间稀疏布置的各阵元并行做单次时间欠采样的苛刻条件下,估计出入射信号的频率和DOA成为可能.相比于现有的联合估计器和稀疏阵列DOA估计方法,本文的联合估计器进一步放松了空、时域的采样限制,降低了硬件成本与计算复杂度.理论分析与仿真实验表明,该算法具有较高的抗噪声性能,故在雷达、遥感等在超高频段以上的被动感知的目标探测领域具有较为广泛的应用前景.未来将会在多目标的频率和DOA联合估计方面做拓展工作.

附录A 闭式鲁棒中国余数定理重构流程

假设有J个余数公约数为M,互素整数为

Γ1,···,ΓJ,因此有Mi=MΓi,i=1,2···,J,按照如下步骤可重构得到

步骤1利用所给余数构造J−1个参数

其中[·]表示四舍五入取整.

步骤2对关于Γi取模,得

其中,bi,1表示γ1/Γi关于Γi的模逆,定义γ1,Γ2···ΓJ.

步骤4通过下式计算出其余J−1个折叠整数

步骤5最终,未知数可以由下式重构得到

[1]Xu L,Li J,Stoica P 2008IEEE Trans.Aerosp.Electron Syst.44 927

[2]Rappaport T S 1996Wireless Communications:Principles and Practice(New Jersey:Prentice Hall PTR Upper Saddle River)p43

[3]Li Y,Seshadri N,Ariyavisitakul S 1999IEEE J.Sel.Areas Commun.17 461

[4]Poisel R 2012Electronic Warfare Target Location Methods(London:Artech House)p224

[5]Gustafsson F 2003International Conference on Acoustics,Speech,and Signal ProcessingHong Kong,China April 6–10,2003 p553

[6]Zatman M,Strangeways H 1995Antennas and Propagation Society International SymposiumNewport Beach,USA,June 18–23,1995 p431

[7]Lemma A N,van der Veen A J,Deprettere E F 1998International Conference on Acoustics,Speech,and Signal ProcessingSeattle,USA,May 15–19,1998 p1957

[8]Liang J,Zeng X,Ji B,Zhang J,Zhao F 2009Digit Signal Process19 596

[9]Lin J D,Fang W H,Wang Y Y,Chen J T 2006IEEE Trans.Signal Process54 4529

[10]Zoltowski M D,Mathews C P 1994IEEE Trans.Signal Process42 2781

[11]Mo ff et A 1968IEEE Trans.Antennas Propag.16 172

[12]Taylor H,Golomb S 1985CSI Tech.Rep5 1

[13]Vaidyanathan P P,Pal P 2011IEEE Trans.Signal Process59 3592

[14]Vaidyanathan P P,Pal P 2011IEEE Trans.Signal Process59 573

[15]Pal P,Vaidyanathan P P 2011Digital Signal Processing Workshop and IEEE Signal Processing Education WorkshopSedona,USA,January 4–7,2011 p289

[16]Liu C L,Vaidyanathan P P 2015IEEE Signal Process.Lett.22 1438

[17]Pal P,Vaidyanathan P P 2010IEEE Trans.Signal Process58 4167

[18]Liu C L,Vaidyanathan P P 2016IEEE Trans.Signal Process64 3997

[19]Liu C L,Vaidyanathan P P 2016IEEE Trans.Signal Process64 4203

[20]Liang H,Zhang H 2012J.Northwestern Polytechn.Univ.28 409(in Chinese)[梁红,张恒 2012西北工业大学学报28 409]

[21]Wang W,Xia X G 2010IEEE Trans.Signal Process58 5655

[22]Tsui J B 2004Digital Techniques for Wideband Receivers(Raleigh:SciTech Publishing)p341

Joint estimation of frequency and direction of arrival under the single-and-parallel spatial-temporal undersampling condition∗

Huang Xiang-Dong1)Liu Ming-Zhuo1)Yang Lin1)Liu Kun2)†Liu Tie-Gen2)

1)(School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China)

2)(School of Precision Instrument and Opto-electronics Engineering,Tianjin University,Tianjin 300072,China)

11 April 2017;revised manuscript

5 May 2017)

As the application frequency is increasingly high,it becomes difficult to design joint estimators for the frequencies and directions of arrival(DOAs)under the spatial-temporal undersampling condition.Specifically,on one hand,the temporal Nyquist theorem requires that the sampling rate be at least twice the highest frequency,which is unfordable for the existing analog-to-digital converters;on the other hand,the spatial Nyquist theorem also requires that each inter-element spacing be less than or equal to half the wavelength,which inevitably results in severe mutual coupling among sensors.To solve these intractable problems,in this paper,we propose a joint estimator based on a co-prime sparse array.Firstly,based on the combination of this sparse array and the closed-form robust Chinese remainder theorem(CRT),the theoretical model for the proposed frequency and DOA joint estimator is built up.Secondly,at each sensor,a frequency estimate for the source object can be calculated through implementing the closed-form robust CRT on two frequency remainders,which are generated by applying the Tsui spectrum correction to the discrete Fourier transform results of two receiver sequences.Then,averaging these estimates at all sensors yields the final frequency estimate.Lastly,on the basis of frequency estimation,the final DOA estimate can be calculated through implementing the closed-form robust CRT on all phase-difference remainders,which are also derived from the Tsui spectrum correction.It needs to be emphasized that the proposed joint estimator possesses two attractive merits.One merit is that due to the fact that the proposed array allows a high sparsity of element-spacings,both the hardware cost and the mutual coupling among sensors can be considerably reduced;the other merit is that compared with the existing estimators,the proposed joint estimator achieves high estimation precision even in the single-and-parallel undersampling condition(i.e.,multi-time undersampling is bypassed in each sensor element,leading to a high data processing efficiency).In particular,this high accuracy attributes to two aspects:1)the Tsui spectum corrector incorporated in the proposed joint estimator can provide high-accuracy remainders for the CRT recovery;2)the closed-form robust CRT itself is unbiased and thus the CRT recovery brings no extra system errors.Numerical results verify that the proposed joint estimator possesses both strong noise robustness and high estimation accuracy,which presents a vast potential application in several passive sensing fields such as radar and remote sensing.

undersampling,direction of arrival estimation,frequency estimation,Chinese remainder theorem

(2017年4月11日收到;2017年5月5日收到修改稿)

随着应用频段的不断升高,空时域欠采样下的入射信号的频率和到达角的联合估计变得愈加困难.为解决此难题,本文提出了一种基于互素稀疏阵列的联合估计器.首先,结合互素稀疏阵列和闭式中国余数定理,建立了频率估计和到达角估计的理论模型;其次,将频谱校正理论和中国余数定理结合起来,导出了频率估计算法;再次,将相位差校正和中国余数定理结合起来,导出了到达角估计算法.该估计器不仅可降低现有估计器的硬件成本,而且仅需对单次并行采样的快拍做并行处理即可获得联合估计结果,无需对单阵元做多次采样,数据处理效率较高.仿真实验表明,该估计器具有较高的鲁棒性估计精度,因而在雷达、遥感等被动感知领域具有较广阔的应用前景.

10.7498/aps.66.188401

∗国家自然科学基金(批准号:61671012,61475114)和国家重大科学仪器设备开发专项(批准号:2013YQ030915)资助的课题.

†通信作者.E-mail:beiyangkl@tju.edu.cn

感谢夏香根教授在闭式鲁棒中国余数定理方面提供的指导.

PACS:84.40.–x,84.40.Ua,07.07.Df,07.50.QxDOI:10.7498/aps.66.188401

*Project supported by the National Natural Science Foundation of China(Grant Nos.61671012,61475114)and the Special Funds of the Major Scientific Instruments Equipment Development of China(Grant No.2013YQ030915)

†Corresponding author.E-mail:beiyangkl@tju.edu.cn