改进的单次散射相函数解析表达式∗
2018-01-11程晨史泽林崔生成徐青山
程晨 史泽林 崔生成 徐青山
1)(中国科学院安徽光学精密机械研究所,中国科学院大气成分与光学重点实验室,合肥 230031)
2)(中国科学技术大学研究生院科学岛分院,合肥 230031)
3)(中国科学院沈阳自动化研究所,沈阳 110016)
改进的单次散射相函数解析表达式∗
程晨1)2)史泽林3)崔生成1)徐青山1)†
1)(中国科学院安徽光学精密机械研究所,中国科学院大气成分与光学重点实验室,合肥 230031)
2)(中国科学技术大学研究生院科学岛分院,合肥 230031)
3)(中国科学院沈阳自动化研究所,沈阳 110016)
散射,相函数,Henyey-Greenstein相函数,新的Henyey-Greenstein相函数
1 引 言
大气辐射传输模型是大气科学研究的主要课题之一,它是联系大气物理属性和辐射属性的重要途径.大气辐射传输模型的主要研究方法有解析数值法和统计模拟法,研究过程中需要考虑大气光学厚度、气体成分的单次散射反照率以及粒子的单次散射相函数,其中散射相函数的准确性和复杂程度直接影响到辐射传输模型的计算结果和计算效率[1−4].因此,对相函数的研究主要集中在缩短相函数的计算时间以及提高相函数的准确性.
目前常用于辐射传输模拟过程中的相函数计算方法有:Legendre多项式展开法、Mie理论递推公式计算方法、相函数调整方法以及Henyey-Greenstein(H-G)相函数近似法[5,6].Legendre多项式展开法主要用于离散纵坐标法求解辐射传输问题中,对于球形小粒子,相函数只需要很少的展开项就可以求解出它的散射问题;对于非球形粒子及大粒子,它们的前向散射峰异常尖锐,需要数千项的展开式才能收敛,且计算复杂、计算量巨大[7,8].Mie散射计算过程中将粒子假设为球体,对Mie理论直接编程时涉及到复变量Bessel函数的计算,因为粒子尺度限制,即使粒子为球形,散射角度也不能由几何光学或者格林公式[9]获得的渐近表达式足够准确的近似[10].相函数调整方法的基本思想是将相函数近似为狄拉克Delta函数和截断相函数的线性组合,并通过相似性原理[11,12]得到新的大气光学参数[13].以上3种相函数计算方法都存在计算时间长、效率低的问题.为减小计算时间、提高计算效率,研究粒子的辐射传输特性时通常使用相函数的近似解析表达式.H-G相函数是最普遍适用的相函数近似解析表达式[14],该相函数公式简单、数值计算方便,便于求解出关于散射角随机抽样的逆函数,可方便地应用于蒙特卡罗方法关于散射方向抽样的问题.但该近似方法仍然存在诸多局限,例如不能很好地描述后向散射问题[15].为了更好地描述不同的物理模型及物理问题提出了多种改进的H-G相函数近似方法,其中为了能很好地模拟后向散射问题,Cornette和Shanks[16]利用Rayleigh相函数与H-G相函数推导出Henyey-Greenstein*(H-G*)相函数.尽管如此,有些情况下H-G*相函数仍不能很好地模拟真实的散射相函数.为了能够得到最大程度符合粒子散射特性的散射相函数,结合Rayleigh相函数和H-G相函数,本文提出了一种新的散射相函数解析式(RH-G*相函数).为了验证RH-G*相函数在描述单个粒子及多分散系粒子散射特性的适用性,综合比较了单个粒子的RH-G*相函数与H-G相函数、H-G*相函数之间的偏离程度,并分析了多种气溶胶模式下RH-G*相函数与多分散系Mie散射相函数、H-G*相函数的吻合度,为更加准确、高效地计算辐射传输特性提供理论支持.
2 散射相函数
散射相函数描述的是入射能量经粒子散射后的能量角分布.入射方向与散射方向之间的夹角θ称为散射角,为了更好地描述散射能量随散射角的变化,有必要引入一个称之为相函数的无量纲参数p(cosθ),

按此定义,相函数是归一化的.按照定义计算粒子的散射相函数,可以保证计算结果的精度,但计算效率不够.为此,研究过程中常采用相函数的解析表达式来近似计算散射相函数.相函数解析表达式的优点是大大提高了计算效率,且在一定程度上符合实际的散射规律,但总体来说计算精度稍有不足[6,16].这就要求发展更加适合实际散射规律的相函数解析表达式.
2.1 Mie散射相函数
借助于振幅散射矩阵,球形粒子的散射相函数p表示为[17]
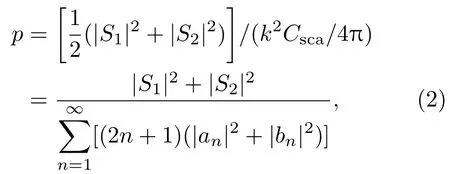
其中,k是波数;是散射截面,X是矢量散射振幅,Ω是立体角;an和bn为复函数;S1和S2为复振幅.S1和S2的计算公式如下:

其中πn和τn为角度依赖函数,可以通过递推关系求解.对于满足f(r)分布的多分散粒子系,散射相函数为[18]

其中p(λ,r,m,θ)是已知粒子尺寸参数及复折射率的单个粒子散射相函数,λ是波长,r是粒子半径,m是复折射率.
2.2 H-G相函数
Mie散射相函数的计算过程比较复杂,为了计算方便,常用表达形式简单、数值计算方便的H-G相函数来替代[10]:
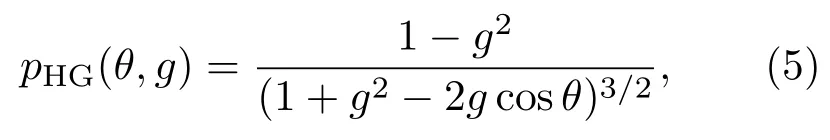
其中θ是散射角,g是不对称因子.H-G相函数可以较好地模拟前向散射峰,但是不能正确模拟后向散射,且当g→0时,该相函数不能还原成瑞利散射相函数:

2.3 双H-G相函数
为了克服H-G相函数不能正确模拟后向散射这个缺陷,Cornette和Shanks[16]提出使用双H-G相函数(DH-G相函数)来近似:

DHG相函数虽然可以较好地体现粒子的散射特征,但是解析式是由3个参数确定的:f是一个正的参数;g1是正值,表示前向散射部分;g2是负值,表示后向散射部分,使用起来比较复杂,不适合实际应用.当g→0时,为了将双H-G相函数还原成瑞利散射相函数,前向散射峰和后向散射峰需要相等,即g1=−g2,且f=1/2,但此时两者之间仍不能很好地符合,最小均方根误差为0.15[16].且H-G相函数、DH-G相函数只用于粒子的尺寸参数不是太小的情况.
2.4 H-G*相函数
为了能很好地模拟后向散射问题,Cornette和Shanks[16]利用Rayleigh相函数与H-G相函数推导出了修正的H-G相函数,即H-G*相函数:

该相函数在一定程度上弥补了H-G相函数和DHG相函数的不足,且只有一个自由参数g,在g→0时,与瑞利散射相函数符合;当g→1时,近似于H-G相函数.
3 本文提出的新的散射相函数
比较H-G*和H-G相函数会发现,H-G*在前向散射部分修正较多,而在后向散射部分修正较少,不能很好地模拟后向散射峰值比较大的粒子的散射特征,例如海洋型气溶胶[18].为了更好地模拟后向散射峰值比较大的粒子的散射特征,对H-G相函数解析式与瑞利散射相函数解析式按照不对称因子进行修正.将新的相函数表示成H-G相函数和瑞利相函数以及不对称因子的多项式的和,其中H-G相函数和瑞利相函数的系数是不对称因子g的多项式.要求在角度大于90◦时,增大后向散射峰值,且在g→0时,新的相函数与瑞利散射相函数符合;当g→1时,新的相函数近似于H-G相函数.基于这些考虑,改进的散射相函数(RH-G*)为

该相函数在一定程度上增大了后向散射峰,解析式形式简单,只有一个自由参数g.
图1给出了不对称因子从0到0.9(间隔为0.1)时,H-G相函数、H-G*相函数和RH-G*相函数随角度变化的数值结果.


图1 (a)—(j)是RH-G*相函数与H-G*相函数、H-G相函数的角分布对比Fig.1.(a)–(j)Comparison of RH-G*phase function,H-G*phase function and H-G phase function.
由图1可知:1)三种相函数角分布变化趋势相同,表现在小角度的前向散射峰值较强,后向散射峰值较弱,且随着不对称因子g的增大,都有前向散射峰增大、后向散射峰减小的趋势;2)相对于H-G相函数和H-G*相函数,RH-G*相函数增大了后向散射的峰值;3)当g=0时,RH-G*相函数和H-G*相函数完全重合,但与H-G相函数偏离程度较大;当g6 0.5时,三种相函数的前向散射峰值显现出很大的差异,但RH-G*相函数与H-G*相函数后向散射部分符合较好;当g>0.5时,则相反.总体来说,RH-G*相函数提高了后向散射峰值.
白璐等[19]提出了由于海洋型气溶胶的后向散射峰值比较大,采用H-G相函数及H-G*相函数难以给出较好的拟合结果;朱孟真等[20]给出了常见或霾天气条件下紫外光散射相函数的比较,结果显示H-G相函数及H-G*相函数的数值在120◦以后与Mie散射的计算结果差别比较大,Mie散射相函数有比较明显的后向散射峰,说明提高相函数解析式的后向散射峰值是很有必要的,RH-G*相函数能够合理地描述单个粒子散射辐射能量随角度的变化.
4 多种气溶胶模式下Mie散射相函数与RH-G*相函数的对比
显然,RH-G*相函数可以很好地描述单个粒子散射辐射能量的角分布特征.相函数还必须能够用于辐射传输问题的求解,因此需要能够模拟多分散系粒子散射能量的角分布.
Derimendjian[21,22]利用Mie散射理论描述了三种气溶胶类型(近似的大陆型霾C(Haze C)、海洋型霾M(Haze M)和积云C.1(Cloud C.1))的散射辐射能量的分布特征.海洋型霾M最初是为海洋线和沿海地区的气溶胶设计的;积云C.1类似薄的积云.近似大陆型霾C是不连续分布的;海洋型霾M和积云C.1是按照指数型公式分布(广义Γ分布):

其中,a表示粒子浓度;r是粒子半径;α,b,γ是依气溶胶种类不同而定的常数.表1列举了这三种气溶胶类型尺寸分布的典型参数.

表1 粒子尺度分布参数Table 1.Particle-size distributions.
非偏振多分散系Mie散射相函数计算过程选取的参数(波长、粒子尺度、复折射率)如表2所列:λ是波长,Re是折射率实部,Im是折射率虚部,参数g是散射不对称因子.

表2 粒子光学参数Table 2.Particle optical properties.
图2—图4给出了积云C.1、近似大陆型霾C和海洋型霾M三种模式下多分散系Mie散射相函数、RH-G*相函数和H-G*相函数的角分布.虚线表示Mie散射相函数;虚线加点表示RH-G*相函数;实线加星号表示H-G*相函数.
图2积云C.1模式中,RH-G*相函数和H-G*相函数的前向散射峰值很接近;波长小于5.3µm时,RH-G*相函数与多分散系Mie散射相函数在后向散射部分的符合程度高.图3近似大陆型霾C模式中,总体而言RH-G*相函数,对多分散系Mie散射相函数的拟合效果要优于H-G*相函数,尤其是在大角度后向散射上.图4中波长大于10µm时,海洋型霾M模式的后向散射峰值采用RH-G*相函数能得到较好的拟合结果.
总之,1)RH-G*相函数弥补了H-G*相函数描述后向散射峰尖锐程度的不足,特别是短波部分;2)RH-G*相函数提高了与多分散系Mie散射相函数的符合程度,特别是在前向散射部分;3)由于粒子尺度通常小于λ=100µm很多,散射相函数近似于瑞利散射相函数,此时RH-G*相函数精确地描述了这一现象,其随角度变化的曲线几乎与多分散系Mie散射相函数的曲线重合;4)对于后向散射特征比较明显的气溶胶模式,RH-G*相函数更接近于Mie散射相函数.


图2 (a)—(j)积云C.1的Mie散射相函数、H-G*相函数与RH-G*相函数的角度分布对比Fig.2.(a)–(j)Comparison of Mie phase function for the Cloud C.1 model,H-G*phase function and RH-G*phase function.

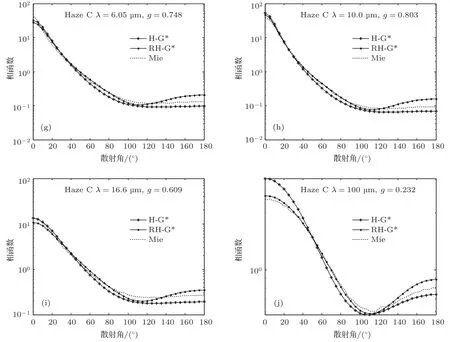
图3 (a)—(j)近似大陆型霾C的Mie散射相函数、H-G*相函数与RH-G*相函数的角度分布对比Fig.3.(a)–(j)Comparison of Mie phase function for the Haze C model,H-G*phase function and RH-G*phase function.
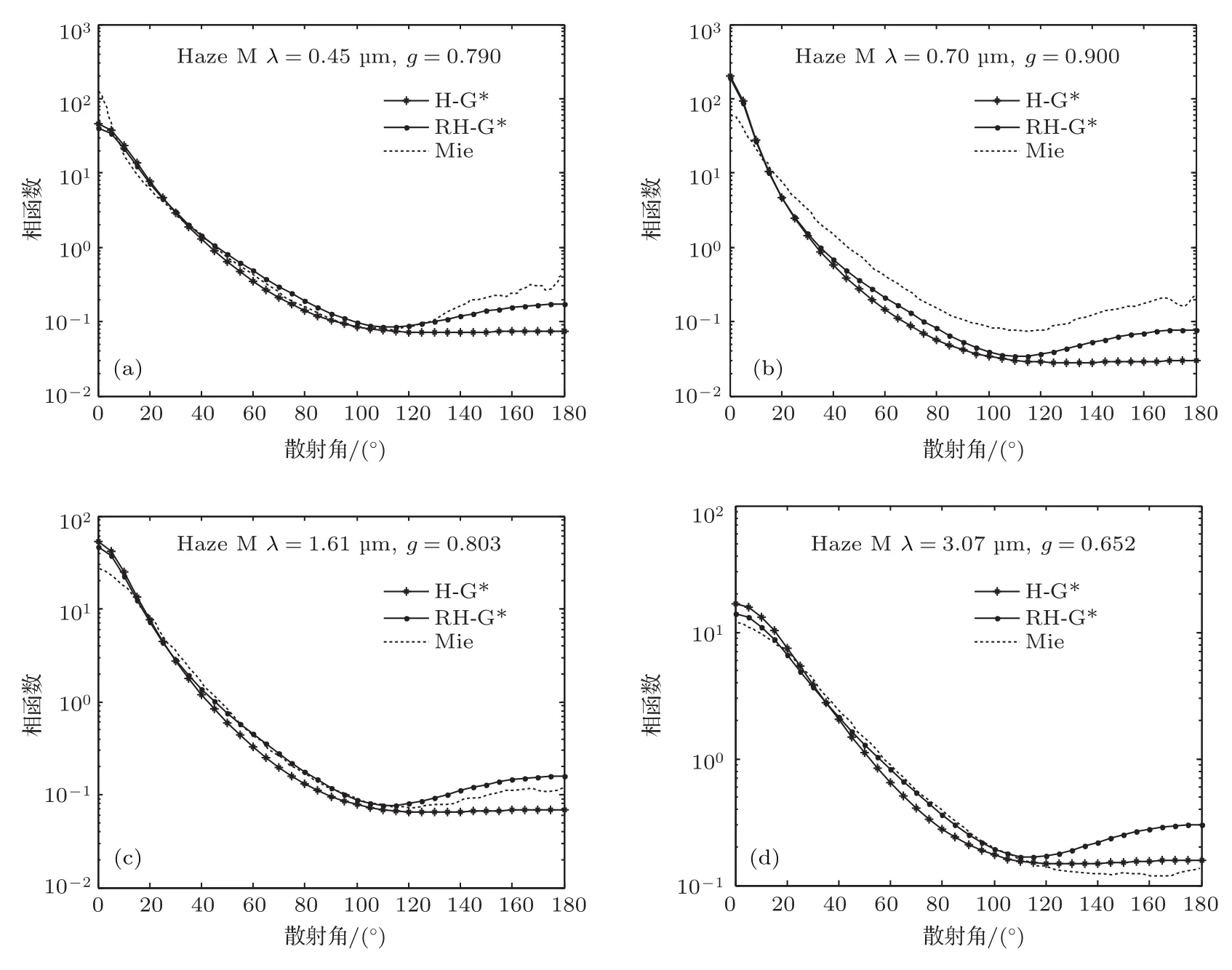
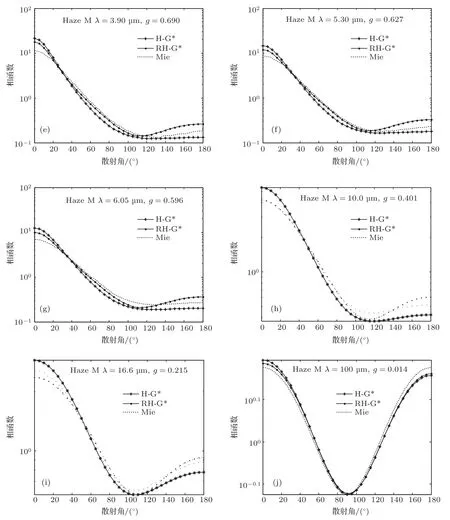
图4 (a)—(j)海洋型霾M的Mie散射相函数、H-G*相函数与RH-G*相函数的角度分布对比Fig.4.(a)–(j)Comparison of Mie phase function for the Haze M model,H-G*phase function and RH-G*phase function.
出现上述结果的原因如下:1)相同波段不同气溶胶类型的相函数计算结果不同,这主要是因为各种气溶胶类型的不对称因子g存在差异,不对称因子主要受粒子尺度因子a(a=πd/λ,d是粒子直径,λ是入射波长)和光学常数折射率的影响,本文中三种气溶胶类型的粒子尺度和折射率不同,所以计算结果存在差异,尺度因子越小,相函数随角度变化曲线的对称性越强,所以波长为100µm时,各个曲线的对称性是最强的;2)相函数解析式与Mie散射相函数的计算结果存在差异的原因是Mie散射相函数是由Mie散射参数和n阶Legendre多项式表示的,Mie散射参数反映了电场振荡和磁场振荡对散射的影响,而相函数解析式中将Mie散射参数近似为与不对称因子有关的多项式,所以RH-G*相函数和H-G*相函数随角度的变化曲线相对比较平滑,且与Mie散射相函数的计算结果存在差异;3)H-G*相函数和RH-G*相函数在相同波段下计算结果存在差异时主要原因在于RH-G相函数是通过H-G相函数与不对称因子和散射角有关的多项式的和来描述散射过程的,不对称因子增大时,RH-G*相函数在前向的修正较多,后向的修正较少,但是前向和后向的值都是增大;H-G*相函数是以不对称因子和散射角有关的多项式作为H-G相函数的系数来描述散射过程的,不对称因子越大,修正的越少,所以RH-G*相函数与H-G*相函数之间存在差异.
为了进一步说明RH-G*相函数提高大角度后向散射的合理性,表3比较了H-G*相函数、RH-G*相函数与多分散系Mie散射相函数在角度大于90◦时的均方根差值.对比时,角度间隔为5◦,均方根误差表示为是散射角θ处不同相函数解析式计算的值,pi(θ)是对应散射角θ下Mie散射相函数的计算值.表中列举出了三种气溶胶模式中,RH-G*相函数与Mie散射相函数的均方根差值小于H-G*相函数与Mie散射相函数的有22个,占总数的73.3%,说明大部分情况下,RH-G*相函数在大角度后向散射上与Mie散射相函数的符合程度较好.因此,RH-G*相函数提高大角度后向散射是合理的、必要的.

表3 多分散系气溶胶粒子H-G*相函数和RH-G*相函数与Mie散射相函数的方均根误差比较Table 3.Comparisons of the root-mean-square error between the RH-G*phase function,the H-G*phase function and the Mie-sacttering phase function.
5 结 论
本文提出了一种新的单次散射相函数(RH-G*相函数)的解析表达式,合理地提高了后向散射峰值,公式简单,计算方便.多种气溶胶模式下,RH-G*相函数与多分散系Mie散射相函数的拟合效果优于H-G*相函数,尤其是后向大角度方向上.RH-G*相函数模拟后向散射峰值比较大的粒子的散射特征有明显的效果,对准确模拟辐射传输过程具有重要意义.但新的相函数不能很好地求解出散射角随机抽样的逆函数,所以不能很好地用于蒙特卡罗方法中.
[1]Si F Q,Liu J G,Xie P H,Zhang Y J,Dou K,Liu W Q 2006Acta Phys.Sin.55 3165(in Chinese)[司福祺,刘建国,谢品华,张玉钧,窦科,刘文清2006物理学报55 3165]
[2]Xie Z L,Zhang R,Xiu X Q,Han P,Liu B,Chen L,Yu H Q,Jiang R L,Shi Y,Zhang Y D 2007Acta Phys.Sin.56 6717(in Chinese)[谢自力,张荣,修向前,韩平,刘斌,陈琳,俞慧强,江若链,施毅,郑有炓 2007物理学报 56 6717]
[3]Li Y,Song J,Zhang Z M 2003Chin.Phys.Lett.20 1189
[4]Li J N,Barker H,Yang P,Yi B Q 2015J.Geophys.Res.120 128
[5]Liu K,Zhang F,Wu K,Zhou X J,Zhang H,Liu R Q 2016Acta Meteorol.Sin.74 784(in Chinese)[刘琨, 张峰,吴琨,周秀骥,张华,刘仁强2016气象学报74 784]
[6]Toublance D 1996Appl.Opt.35 3270
[7]Chen X H,Liu Q,Wei H L 2007J.Light Scatt.3 283(in Chinese)[陈秀红,刘强,魏合理 2007光散射学报 3 283]
[8]Ding S,Xie Y,Yang P,Weng F,Liu Q,Baum B,Hu Y 2009J.Quant.Spectrosc.Radiat.Transfer110 1190
[9]Cai H,Huang N N 2003Chin.Phys.Lett.20 496
[10]Xu L Q,Li H,Xiao Z Y 2008Acta Phys.Sin.57 6030(in Chinese)[徐兰青,李晖,肖郑颖 2008物理学报 57 6030]
[11]Liou K N(translated by Guo C L,Zhou S J)2004An Introduction to Atmospheric Radiation(2nd Ed.)(Beijing:China Meteorogical Press)pp108–109(in Chinese)[廖国男 著(郭彩丽,周诗健 译)2004大气辐射导论(第二版)(北京:气象出版社)第108—109页]
[12]Joseph J,Wiscombe W,Weinman J 1976J.Atmos.Sci.33 2452
[13]Wiscombe W 1977J.Atmos.Sci.34 1408
[14]Huang C J,Liu Y F,Wu Z S,Sun Y Q,Long S M 2009Acta Phys Sin.58 2397(in Chinese)[黄朝军,刘亚峰,吴振森,孙彦清,龙姝明2009物理学报58 2397]
[15]Kattawar G W 1975Quant.Spectrosc.Radiat.Transfer15 839
[16]Cornette W M,Shanks J G 1992Appl.Opt.31 3152
[17]Bohre C F,Hu ff man D R 1983Absorption and Scattering of Light by Small Particles(New York:John Wiley)p100
[18]McCartney E J 1988Optics of the Atmosphere(Beijing:Science Press)p276(in Chinese)[麦克特尼 E J著 (潘乃先译)1988大气光学(北京:科学出版社)第276页]
[19]Bai L,Tang S Q,Wu Z S,Xie P H,Wang S M 2010Acta Phys.Sin.59 1749(in Chinese)[白璐,汤双庆,吴振森,谢品华,汪世美2010物理学报59 1749]
[20]Zhu M Z,Zhang H L,Jia H L,Yang J K,Cheng S L 2007J.Light Scatt.3 225(in Chinese)[朱孟真,张海良,贾红辉,杨建坤,常胜利2007光散射学报3 225]
[21]Derimendjian D 1963Scattering and Polarization Properties of Polydispersed Suspensions with Partial Absorption(New York:The MacMillan Company,Pursuant to a Special Arrangement with Pergamon Press)pp4–9
[22]Diermendjian D 1969Electromagnetic Scattering on Spherical Polydispersions(New York:American Elsevier)pp31–78
Modi fied analytic expression for the single-scattering phase function∗
Cheng Chen1)2)Shi Ze-Lin3)Cui Sheng-Cheng1)Xu Qing-Shan1)†
1)(Key Laboratory of Atmospheric Composition and Optical Radiation,Anhui Institute of Optics and Fine Mechanics,Chinese Academy of Sciences,Hefei 230031,China)
2)(Science Island Branch of Graduate School,University of Science and Technology of China,Hefei 230031,China)
3)(Shenyang Institute of Automation Chinese Academy of Sciences,Shenyang 110016,China)
6 April 2017;revised manuscript
11 May 2017)
In electromagnetic radiative transfer calculation,the accuracy and the computation time are usually determined by the representation of single-scattering phase function.Accurate calculation is time consuming even for spherical particle,thus,an analytic representation is commonly adopted to approximate the exact phase function and then accelerate the calculation.Most widely used single-scattering phase functions are the Henyey-Greenstein phase function and modi fied Henyey-Greenstein phase function(Henyey-Greenstein*).Although the Henyey-Greenstein phase function and the Henyey-Greenstein*phase function can represent the forward-scattering peak of Mie-scattering phase function well,they fail to reproduce the backscattering behavior,limiting the accuracy of the calculation.In order to better fit exact calculations and simulate the backward-scattering peak,we develop a new analytic expression based on the fundamental theory of electromagnetic scattering and radiation transmission.This phase function is an algebraic expression with one single free parameter(asymmetry factor),and can be expanded into Legendre polynomials.The new phase function converges to the Rayleigh phase function when the asymmetry factor approximates to 0,and it can approach to the Henyey-Greenstein phase function as the asymmetry factor is about 1.We compare the Henyey-Greenstein phase function,the Henyey-Greenstein*phase function,and the new phase function for different asymmetry factors,and f i nd that the new phase function provides a more realistic description for the unpolarized light scattering from small particles.Furthermore,the calculated value for the ratio of the scattering intensity at 90 degree to that in the backward direction is more reasonable.We also investigate the effectiveness by approximating the scattering from polydispersed particles through comparing the new phase function,the Henyey-Greenstein*phase function,and the Mie-scattering phase function for three types of Derimendjian’s polydispersions.Results show that the new phase function fits the Mie-scattering phase function much better than the Henyey-Greenstein*phase function.For the new phase function,the root-mean-square error is small for 73.3%data.By contrast,only 26.7%data fit the Mie-scattering phase function well for the Henyey-Greenstein*phase function.Similarly,the effectiveness of new function is most significant when calculating the ratio of the scattering intensity at 90 degree to that in the backward direction.In summary,the new Henyey-Greenstein*phase function provides a more accurate calculation for the scattering intensity in the backward direction,and is conducive to electromagnetic radiative transfer calculation.Furthermore,because the proposed phase function has the same basic form as the Heny-Greenstein phase function,reformatting radiative transfer model in terms of the new phase function should require relatively little effort.
scattering,phase function,Henyey-Greenstein phase function,new Henyey-Greenstein phase function
PACS:02.30.–f,03.65.Nk,07.60.Rd,42.25.BsDOI:10.7498/aps.66.180201
*Projectsupported by the ChinaSpecial Fund for Meteorological Research in the Public Interest(Grant No.GYHY201106002-03)and the National Natural Science Foundation of China(Grant No.41576185).
†Corresponding author.E-mail:qshxu@aiofm.ac.cn
(2017年4月6日收到;2017年5月11日收到修改稿)
单次散射相函数对电磁辐射传输模拟过程的准确性和计算效率有重要的影响.基于电磁散射与辐射传输中的基本理论,对单次散射相函数的解析表达式进行了研究,提出了一种新的单次散射相函数解析表达式.比较了单个粒子的Henyey-Greenstein相函数、Henyey-Greenstein*相函数与新的相函数随角度的分布,发现新的散射相函数提高了后向散射峰值,可以更合理地描述单个粒子的散射特性.按三种气溶胶粒子谱分布模式计算了Henyey-Greenstein*相函数和新的相函数对应的数值结果,并与多分散系Mie散射相函数进行对比,发现新的相函数提高了与多分散系Mie散射相函数的符合程度.研究表明,对于大角度(大于90◦)后向散射,新的相函数与Mie散射相函数均方根差较小的占73.3%,高于Henyey-Greenstein*相函数的26.7%,证明了新的相函数可以显著提高后向散射峰值.新的相函数对准确模拟辐射传输过程具有重要意义.
10.7498/aps.66.180201
∗气象专项课题(批准号:GYHY201106002-03)和国家自然科学基金(批准号:41576185)资助的课题.
†通信作者.E-mail:qshxu@aiofm.ac.cn
