基于LADRC的反渗透海水淡化温控系统①
2018-01-11刘宏利刘世佳俞永江陈小奇
刘宏利 刘世佳 康 权 俞永江 邵 磊 李 季 陈小奇
(1.天津理工大学天津市复杂系统控制理论及应用重点实验室;2.国家海洋局天津海水淡化与综合利用研究所)
基于LADRC的反渗透海水淡化温控系统①
刘宏利1刘世佳1康 权2俞永江2邵 磊1李 季1陈小奇1
(1.天津理工大学天津市复杂系统控制理论及应用重点实验室;2.国家海洋局天津海水淡化与综合利用研究所)
针对反渗透海水淡化系统中温度参数的非线性、时变、迟滞及存在扰动等特点,采用线性自抗扰(LADRC)控制器建立反渗透海水淡化温控系统。设计LADRC控制器可实现输入对输出的实时跟踪和实时补偿,并利用李雅普诺夫稳定性方法证明了该一阶LADRC中二阶线性扩张状态观测器LESO的稳定性问题。仿真结果表明:LADRC控制比PID控制响应速度更快,稳态精度更高,抗干扰能力更好,对整个系统稳定高效运行、降低系统能耗,有着重要的实用价值和研究意义。
反渗透 LADRC控制 LESO 温度控制 李雅普诺夫稳定性
水资源短缺已经成为全球性问题,而海洋占地球上所有水的97%,所以海水淡化成为解决水资源匮乏最具发展前景的一种途径[1]。海水淡化主要分为热法和膜法,热法主要为多效蒸馏和多级闪蒸,膜法主要为反渗透、电渗析和纳滤[2]。而反渗透以投资省、能耗低(无相变)、建设周期短及占地少等优点,在全球海水淡化装机总量中占主导地位。
反渗透海水淡化过程直接或间接地受到多种因素的影响,如操作压力、操作温度、水质、浓差极化、结垢程度及膜特性等。在这些因素中,工作温度显著地影响整个过程的性能[3]。因此,需要优化反渗透海水过程中的工作温度,使它恒定保持在一个最优值,以提高反渗透海水淡化的整体效率,降低系统能耗。
常用控制算法为传统PID控制,该控制方法结构简单,但对温度这样的大时滞系统并不能达到很好的控制效果。还有PID与智能算法的结合,如模糊控制算法[4]、遗传(GA)算法[5]及BP神经网络算法[6]等,这些控制算法的稳态精度以及对扰动的抗扰控制效果并不好。笔者采用线性自抗扰控制器(LADRC)控制算法,对温度能达到很好的稳态控制效果,抗干扰能力强,可为系统稳定高效运行提供保障。
1 反渗透海水淡化过程中的模型分析
反渗透过程中的溶解-扩散模型为[7]:
式中Aw、Bs——水渗透系数与盐渗透系数;
Cjm、Cjp——反渗透膜在进料侧和渗透侧的盐浓度;
Js、Jw——盐渗透通量和水渗透通量;
Δp——膜层两侧的压差;
Δπ——反渗透膜的渗透压。
因为进料温度增加不仅导致渗透压Δπ增加,而且导致水的粘度降低。在反渗透海水淡化过程中,如果膜两侧压差Δp是一个定值,则过程的净驱动力(Δp-Δπ)会降低,水渗透通量也会降低。另外,水粘度降低,RO膜的渗透性增加。由于以上这些效应,在反渗透海水淡化过程中更高的温度导致渗透流量和总溶解固体TDS增加[8]。因此,需要对温度进行控制,使它保持在一个最优的恒定值,从而提高系统运行整体效率,降低系统能耗。
2 线性自抗扰控制器的设计
2.1 线性自抗扰控制器的基本控制思想
LADRC继承了自抗扰控制器(ADRC)利用误差反馈进行控制的思想,它省去了自抗扰控制器中的跟踪微分器(TD),而且扩张状态观测器(ESO)和非线性误差反馈(NSEF)都采用线性函数[9]。
一阶线性自抗扰控制器的结构框图如图1所示,其被控对象的结构为单输入单输出(SISO)结构,框图中的参数kp、b0和线性扩张状态观测器(LESO)中的参数ω0为3个待整定的控制参数。其中kp为比例常数,ω0为观测器带宽,b0为扰动补偿因子。
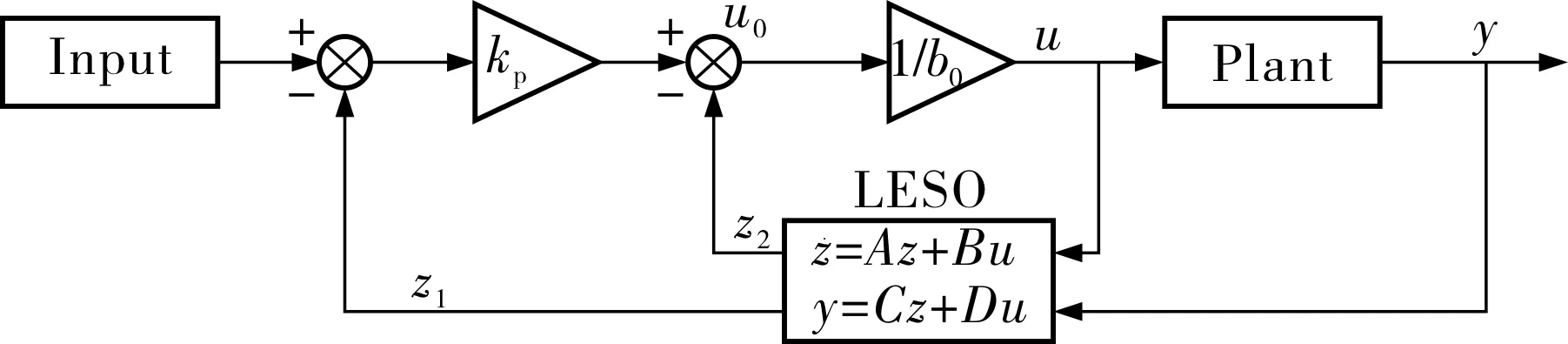
图1 一阶线性自抗扰控制器结构框图
LESO为状态空间方程标准形式:
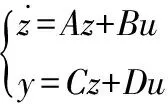
C=I2×2
D=02×2
其中,z为状态观测向量,z=[z1z2]T;y为系统输出;u为系统输入。
对于被控对象为一阶的系统,通过调整3个控制参数(kp、ω0和b0)可以保证整个系统有界输入有界输出(BIBO)稳定。
2.2 基于LADRC的反渗透恒温供水系统设计
考虑到该系统温度参数具有时滞性,存在扰动等,采用LADRC控制器可以有效减少时滞对系统产生的影响,而且不需要精确的数学模型,还可以实时补偿扰动。系统控制回路如图2所示。

图2 恒温控制回路
2.3 稳定性分析
由图1可知该算法是一个带反馈的闭环控制算法,存在稳定性问题,针对文中的一阶模型对它进行稳定性证明(在扰动给定的情况下)。
系统的LESO为:
(1)
L为观测器增益向量,选取增益为:

(2)

(3)

定义李雅普诺夫函数V(ε)=εTPε,则:
(4)
(5)

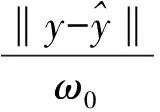
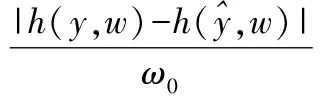
(6)
根据李雅普诺夫渐进稳定性的意义,有:
(7)
LSEF采用的是P控制率,本文的控制率u0为:
u0=kp(v-z1)
(8)
式中kp——比例常数;
v——输入值。
此时,u0是误差反馈控制量,但并不包括对扰动估计值的补偿。在上文已设计的二阶 LESO的基础上加入对扰动补偿的考虑,最终的控制量u可取为:
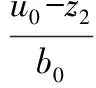
(9)
由式(8)、(9)可得:
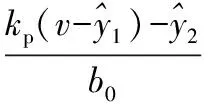
(10)
设e=v-y1,由式(10)得:
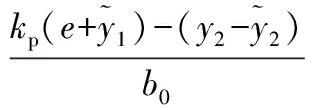
(11)
(12)
完整的线性自抗扰控制器中有跟踪微分器这个环节,这个环节的作用是安排理想的过渡过程并给出过渡过程的微分信号[10]。但考虑到时滞对象本身就反应延迟,所以去掉跟踪微分器。则系统变为:
(13)
式 (13) 写成状态空间的形式为:
(14)

对于稳定性的分析,得出线性自抗扰控制器稳定的条件,为参数整定提供了可靠的理论基础[10]。
3 仿真与结果分析
搭建系统的Simulink仿真系统模型,将反渗透海水淡化系统中的温度换热过程抽象成一阶惯性环节[11]:

式中Kw——系统放大倍数;
Tw——供水系统惯性时间常数;
τ——系统纯滞后时间。
用阶跃信号来模拟反渗透海水淡化过程中的温度,根据现场实验数据,取Kw=1、Tw=500对线性自抗扰控制器进行仿真,同时搭建PID控制,两者进行对比。
LADRC和PID控制下的系统仿真结果如图3所示。

图3 LADRC和PID控制下的系统仿真结果
用白噪声作扰动信号,系统仿真结果如图4所示。

图4 加入扰动后的仿真结果
从以上仿真结果可以看出,LADRC控制比PID控制达到稳态所用的时间短,过程中无超调现象,稳态精度高,加入扰动后PID控制波动较大,LADRC对干扰信号能实时作出补偿,误差在规定范围之内,抗干扰能力强。
4 结束语
针对反渗透海水淡化温控系统这样一个非线性、大时滞的复杂控制系统,LADRC控制器对温度的稳态控制更好,响应速度更快,稳态误差小,可以使系统更快、更准地达到稳态,避免其他能耗,并且利用LESO对扰动进行实时估计,然后将它用于反馈控制中,达到快速消除扰动的目的,抗干扰能力强,满足了反渗透海水淡化水温控制的要求,为反渗透海水淡化系统稳定高效运行提供了保障,为系统能耗的降低提供了保障,具有较强的实用价值。
[1] 郑智颖,李凤臣,李倩,等.海水淡化技术应用研究及发展现状[J].科学通报, 2016, 61(21):2344 ~ 2370.
[2] 满曰南,王晓娟,王银涛,等.海水淡化技术研究新进展和发展趋势[J].工业水处理,2014, 34(11):8 ~ 12.
[3] 孙毅,郑增建,单继宏,等.基于船用反渗透海水淡化装置的压力与温度参数优化[J].浙江工业大学学报,2016, 44(4):359 ~ 363.
[4] 赵阳,曲兴华,李睿.基于模糊算法的自调整温度控制系统[J].天津大学学报, 2011, 44(1):73 ~ 78.
[5] 傅晓云,方旭,杨钢,等.基于遗传算法的PID控制器设计及仿真[J].华中科技大学学报(自然科学版), 2012,40(5):1 ~ 5.
[6] 屈毅,宁铎,赖展翅,等.温室温度控制系统的神经网络 PID 控制[J].农业工程学报,2011, 27(2):307 ~ 311.
[7] 江爱朋,程文,王剑,等.全流程卷式反渗透海水淡化系统操作优化[J].化工学报,2014, 65(4):1333 ~ 1343.
[8] Seungjoon K, Younggeun L,Sanghoun O,et al.Energy Saving Methodology for the SWRO Desalination Process: Control of Operating Temperature and Pressure[J].Desalination,2009,247(1):260 ~ 270.
[9] 吴超,王浩文,张玉文,等.基于LADRC的无人直升机轨迹跟踪[J].航空学报,2015, 36(2):473 ~ 483.
[10] 马幼捷,赵健,周雪松,等.并联混合型有源电力滤波器的线性自抗扰控制及稳定性分析[J].电网技术,2012, 36(11):211 ~ 216.
[11] 邢健峰,纪志成. 基于模糊PID的Smith预估碱液温控系统[J].自动化及仪表,2014, 29(7):43 ~ 47.
TemperatureControlSystemforReverseOsmosisSeawaterDesalinationBasedonLADRC
LIU Hong-li1, LIU Shi-jia1, KANG Quan2, YU Yong-jiang2, SHAO Lei1, LI Ji1, CHEN Xiao-qi1
(1.TianjinKeyLaboratoryofControlTheory&ApplicationinComplicatedSystems,TianjinUniversityofTechnology; 2.SOATianjinInstituteofSeawaterDesalinationandMultipurposeUtilization)
Considering nonlinearity, time-varying, hysteresis and disturbance of the temperature parameters in reverse osmosis desalination system, adopting the linear active disturbance rejection control (LADRC) to establish a temperature control system for reverse osmosis searwater desalination was implemented, in which, having LADRC controller designed to realize real-time tracking and compensation of input to output, and the Lyapunov stability method adopted to prove stability of second order linear expansion state observer (LESO) in the first-order LADRC. The simulation results show that, the LADRC control outperforms the PID control in the response speed, steady-state precision and anti-interference abilities. It has practical value and significance in investigating the whole system’s steady and efficient operation and reducing the energy consumption of the system.
RO, LADRC control, LESO, temperature control, Liapunov stability
天津市科技计划项目(15ZXZNGX00140);天津市应用基础研究计划项目(16JCTPJC49400)。
刘宏利(1975-),副教授,从事控制科学与工程、检测技术与自动化装置、物联网和自主机器人的研究。
联系人刘世佳(1993-),硕士研究生,从事控制科学与工程、检测技术与自动化装置、物联网和自主机器人的研究,984875777@qq.com。
TH865
A
1000-3932(2017)12-1106-04
2017-08-10,
2017-10-31)
