我们的小学数学课堂可以再慢一点
2018-01-11江苏省苏州市吴中区木渎姑苏实验小学
江苏省苏州市吴中区木渎姑苏实验小学 蒋 欣
【存在现象】
现象一:有的老师在课堂教学中(尤其是上公开课),课前制作了十分精美的多媒体课件,当堂的演示也十分生动,整个展示过程可以说完整又严密,老师本以为这种顺风顺水的课堂很好地达成了预期的目标。可是,课后再请同学们讲述时,大部分被提问的同学往往是只能反馈其中的只言片语,且讲不到本质。
现象二:在公开课上,老师最担心学生没反应或者答不出自己心目中的标准答案,“是不是”“对不对”几乎成了口头禅,而学生的回答则是一片随声附和,“是”、“不是”、“对”、“不对”,营造出一个表面热闹踊跃的课堂。
现象三:有的老师将“有效课堂”片面地理解为学生能当堂“高效地”完成大量的练习,于是在一堂课上刻意地组织全体学生必须完成各种层次的练习题,这样程式化地走完教学设计。
【粗浅分析】
上述现象的存在,主要是由于课堂教学任务重,知识点多,而老师片面地追求课堂教学的“即效”,因此往往不给学生思辨、动手操作的时间,而是采取“短平快”的问答式教学,如果学生回答不上来,教师就自问自答——自己将全过程呈现出来。或者进行高密度的训练,课堂上充满着计算公式、解题方法的强化练习,表面上看课堂容量够大,学生短时间内掌握了解题技巧。这种快餐式的教学,虽然学生也很积极,但实际上学生只是学习的机器,只能盲目地跟着老师的预设高速运转,其思维主动性与创造性并没有得到有效发展。这样的教学可能夯实了“双基”(基本知识与基本技能),但是学生没有足够的时空去感悟数学思想方法,也没有有效地积累基本活动经验。
【几点尝试】
教育与其他行业有着本质的区别:教育不是一蹴而就的,否则就会“欲速则不达”,它是一个让智慧思考伴随始终的过程。然而在我们的小学数学课堂教学中,依然存在着过于追求“即效”的现象。下面,笔者结合自己的几个教学案例谈几点尝试与思考。
一、课堂慢一点,或许可以收获“意外的通道”
叶澜教授曾对关于课堂的动态生成说过一句令人回味的话:“课堂应是向未知方向挺进的旅程,随时都有可能发现意外的通道和美丽的图景,而不是一切都必须遵循固定线路而没有激情的行程。”
我们在课堂教学中,不能急于追求快速到达“行程”的终点,而要引领学生漫步于“向未知方向挺近的旅程”,这样或许会收获“意外通道”,领略“美丽图景”。
如我在教学“判断一个分数能否化成有限小数”时,曾偶遇过这样的“美丽图景”。以下是相关教学片段:
学生独立完成后反馈,发现有的分数能化成有限小数,有的则不能化成有限小数。教师指出不能化成有限小数时,一般保留三位小数。
生(突然举手,急于发言):如果一个分数能改写成分母是10、100、1000……的分数,那么它就能化成有限小数,否则就不能化成有限小数。(其余学生沉默片刻后点头示意)
师:这可是个重大发现,真的是这样吗?我们再找几个分数试试看。
师:看样子,一个分数能否化成有限小数,与它的分母有关(学生点头示意)。那为什么分母是6、14等这样的分数无法改写成分母是10、100、1000……的分数呢?
生:像6这个数只能扩大成30、60、90或者300、600、900等,就是无法扩大为10、100、1000。
生:可能是因为6里面含有3,所以无法扩大为10、100、1000……这样的数。
师(追问):为什么含有质因数3就不能扩大成10、100、1000……了呢?
生:因为在10、100、1000……这些数里只含有质因数2和5。
师:对今天研究的知识,我们又有了更新的、更深层的发现。那么,对于这两个分数,又是谁在“作怪”呢?
生:因为它们的分母中含有7、3、11这样的质因数,所以无法扩大为10、100、1000……
师:再看看自己举例的分数,我们的“发现”有道理吗?
学生通过验证,无一例外。
师:既然如此,我们以后判断一个分数能否化成有限小数,是否还要看它能否改写成分母是10、100、1000……的分数,有没有更简捷的方法?
生(交流后):不需要改写,只要直接看一个分数的分母是否含有2、5以外的质因数即可。
生(补充):如果分母中含有2、5以外的质因数,那么这个分数就不能化成有限小数,否则就可以化成有限小数。
生(再次补充):这个分数应该是最简分数。
……
这完全走出了我原来的设计,也“打乱”了我原有的教学节奏,于是我放慢了教学节奏,针对学生提出的看法进行因势利导,正是这个“节外生枝”,才收获了这个探究过程的“意外通道”。
二、课堂慢一点,可以为学生的探究而“留白”
在小学数学课堂教学中,我们提倡引领学生参与学习活动,力求体现学生的主体地位,留给学生一片自主探究的空间,让他们经历知识的发现、问题的提出与思考、规律的探索、结论的表达等活动过程。这就需要我们教师在教学中学会等待,学会“留白”,并在“留白”处等待学生进行丰富多彩的自主探究活动,在“留白”处让学生的探究潜能获得充分的释放。
下面以教学《圆锥体积》为例,谈谈自己的做法。
圆锥体体积的计算方法是由圆柱体的体积计算方法通过实验推导得出来的,其中包含“等底等高”和”两个要点。在教学这一内容(推导体积计算公式)时,若是简单地组织全班同学看教师的演示实验,一段时间后,学生总是丢三落四。在解决有关圆锥的实际问题或辨析相关概念时,不是忘记比较底和高,就是忘了乘因此,我在教学这一计算公式推导时,放慢了节奏。首先组织学生分组实验,各组中圆柱和圆锥的组合是多样的——有的等底等高,有的不是等底等高。然后组织实验操作,实验后汇报交流结果,结合五花八门的实验结果,反思实验、寻找原因、发现联系,从而引导学生发现:在等底等高的情况下,圆锥的体积时圆柱体积的这样,让学生亲身经历了实验过程,他们很容易推导出圆锥的体积公式,有利于防止学生在计算圆锥体积时漏乘这一现象的发生。各组中不同圆柱圆锥的搭配,又很好地防止学生认为圆锥的体积就是圆柱体积的这一错误的发生。
“听过了,就忘记了;看过了,就明白了;做过了,就理解了。”在上述“圆锥体积公式推导”的教学中,我摒弃了单靠教师演示实验,学生观察、发现的教学模式。虽然在课堂上似乎浪费了一定的时间,学生也少练了几道题目,但是学生收获的不只是一个抽象的计算公式,而是明白了计算公式的由来,积累了探究几何图形计算公式的基本活动经验。这一切都需要我们在课堂教学中放慢教学节奏,为学生提供探索的材料,给学生留下足够的时空。
三、课堂慢一点,能使学生的思考更加深刻
在教学解决问题的策略这一领域的内容时,必须引领学生经历某种(或几种)方法来解决此类问题的过程,而这个过程绝不能走过场,必须实实在在地开展探索活动。这就要求我们在课堂上必须给学生足够的时间,学生才能不断调整策略,通过逐步探索,有效地找到合理的解决问题的策略。
下面是笔者关于六年级下册《解决问题的策略——假设》的处理方法。
教学例题时,我放手让学生进行猜测——可能有几只大船?几只小船?结合学生的猜测,整理成下表:(每只大船做5人,每只小船做3人)
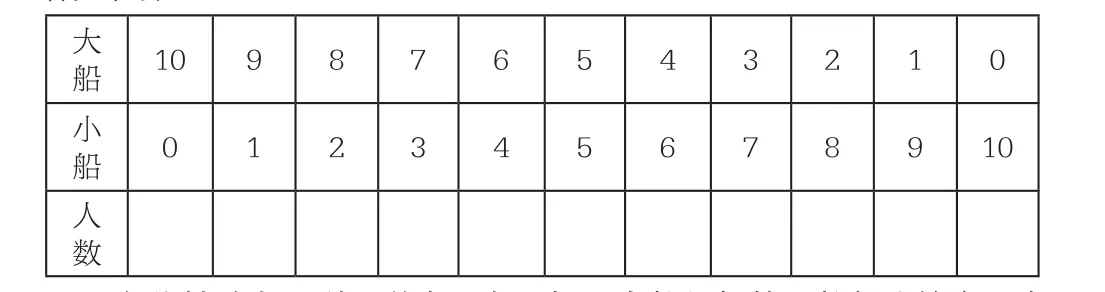
大船 10 9 8 7 6 5 4 3 2 1 0小船 0 1 2 3 4 5 6 7 8 9 10人数
在此基础上,引导学生思考:如果人数与船的只数都比较多,有没有什么好的方法?学生提出可以假设大船与小船各一半,可以2只2只、3只3只甚至5只5只隔着调整。我在组织反馈、引导验证、给予肯定的基础上,再次提出:还有没有别的方法呢?于是就有了下面的教学片段:
师:我们再看黑板上的表格,假设租的都是大船时,能坐几个人?
生:50人。
师:实际呢?和实际人数相比,发生了什么变化?
生:多了8个人。
师:怎么会多了8个人呢?
生:因为把其中的一些小船当成了大船,所以能坐的人就多了。
师:那么1只小船当成1只大船,就会多坐几个人呢?
生:2人。
师:那么多了8个人,说明有几只小船呢?
教师一边引导一边列式:(学生叙述每个算式的含义)5×10=50(人),50-42=8(人),8÷(5-3)=4(只)。
师(上述方法验证后):如果假设全是小船,你能解决吗?
……
可见,我们的课堂教学需要慢一点。课堂慢一点,多给学生一次“异想天开”的机会,我们的课堂探究或许会收获一个“意外的通道”;课堂慢一点,多给学生一次动手操作的机会,我们教学目标的达成度就会更高;课堂慢一点,多给学生一次思辨的机会,学生的思维就会走向更深处。
