数学归纳法的教学实践与思考

福建省福安市第二中学 阮云庆

数学归纳法是数学证明中的一种重要方法，其证明过程的两个步骤缺一不可。通过反复练习与强调也难以把握这一方法的实质，体会其辩证的思想策略和内涵。为什么证题时一定要分两步进行？为什么证了这两步之后能对无穷多个自然数结论成立？学生感到困惑、茫然。除了学生的思维和认识上的局限外，另一个重要原因是教师对教材处理不当引起的。以下谈谈自己的教学实践与思考。

一、理解数学归纳法原理的内涵

1.数学归纳法两个步骤的辩证关系

数学归纳法是通过“有限”来解决“无限”的一种递推证明方法。它的证明有两个步骤，第一步是递推的基础，第二步是递推的依据，两者之间的抽象关系是学生认知的障碍。如何将学生原有的经验转换成适合于新情况所需要的认知结构，一个简捷的途径是：将现有的认知结构融合新知识，把新知识同化于现有认知结构。因此，我将原理想象成一个游戏模型或多米诺骨牌，将一排录音磁带按适当距离竖直排列，以磁带倒下表示命题正确，推倒第一块（表示n取第一个值n0时，命题正确），要保证所有的磁带都倒下（n∈N时命题正确）必须满足什么条件？每一块倒下（n=k，k∈N,k≥n0时命题正确），都能保证其后面的一块倒下（n=k+1时命题正确），从而使数学归纳法的本质直观化。

2.验证n取第一个值时命题正确的必要性

由于教师强调，学生自然认同数学归纳法的两个步骤，但对验证值取第一个值时命题正确的必要性的认识可能还不够深刻，需要设计如下式子的证明，帮助学生体会初始值验证的重要性。

证明：2+4+6+…+2n=n2+n+1(n∈N)。

学生：假设当n=k时，等式成立，即2+4+6+…+2k=k2+k+1，则当n=k+1时，2+4+6+…+2k+2(k+1)=k2+k+1+2(k+1)=(k+1)2+(k+1)+1，∴n=k+1时，等式成立。所以对所有的正整数n，都有等式成立。

学生并没有认识到递推基础的重要性，只知数学归纳法的步骤，而没有领悟到原理和实质。所以在数学归纳法的教学实践中遇到学生种种的错误或困难是很正常的。

二、递推过程中的证题技巧与方法

数学归纳法应用于五类问题的证明，即恒等式、整除性问题、条件等式、不等式和某些几何问题的证明，从证题模式看似乎简单、呆板，其实在递推过程中体现出的证题技巧、方法和数学思想，对培养学生的逻辑思维能力和解题能力却不容置疑。其基本思路是：从归纳假设出发，分析P(k)与P(k+1)的差异及联系，利用折项、添项、放缩、作差、分析等手段，或从P(k+1)中分离出P(k)再进行局部调整，也可以考虑寻求二者的“接口”，以便过渡。其中体现了高超的数学技巧和丰富的数学思想方法以及对学生的能力要求和教师的教学技能的挑战。

例1 当n∈N,n≥2时，求证：

证明：（1）当n=2时，不等式成立。

（2）设n=k时，不等式成立,即则n=k+1时，（学生往往以为“n=k”到“n=k+1”增加一项），∴n=k+1时，不等式成立。

由（1）（2）可知对于任意n∈N(n≥2)，不等式都成立。

三、错误辨析的教学环节

数学归纳法的证题步骤学生较易接受，但对原理的理解要靠方法来揭示和解决，巧妙地设计一些典型的证题错误进行辨析，可提高教材实质性内容的深度，引发学生在认识上产生适当的“矛盾”和“冲突”，使他们发觉在理解数学归纳法时还存在下列不当之处。

证明：（1）当n=1时，结论正确。

（2）设n=k时，结论正确，即成立，则n=k+1时，

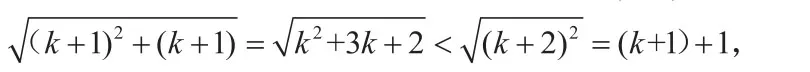
当n=k+1时，结论成立。

所以由（1）（2）可知，对于任意n∈N，都有

上面的解法貌似是数学归纳法，但第二步骤推理没有运用n=k时的归纳假设，这种推理实质上是没有根据的，缺失传递性。

例3 对任意的自然数n，求证：

证明：（1）当n=1时，不等式显然成立。

（2）假设n=k时，不等式成立，即则n=k+1时,

∴n=k+1时，不等式成立。

由（1）（2）可知，对任意的自然数n,都有

在第一步验证n=n0后，数学归纳法要求第二步所考虑的k必须满足k≥n0,本题第二步成立要求k≥2,因此必须依次验证n=1和n=2时不等式成立。

证明:（1）当n=1时，a1=1，所以不等式成立。

（2）假设n=k时命题正确，即有成立，则n=k+1时，

∴n=k+1命题正确。

所以由（1）（2）知对于任意n∈N，都有命题正确。

分析：上述证明犯了偷换归纳假设错误，假设当n=k时，与 当n=k+1时中的 不同取值，于是不能将作为归纳假设进行递推。由则应用此不等式结合分析法实施转化才是正理。

4.猜想与证明

数学命题的论证通常始于不完全归纳，再加以逻辑推理的证明。数学归纳法从论证的方法上综合了归纳和演绎，这种通过“观察—归纳—猜想—证明”发现问题和解决问题的方法，是培养学生探索新问题、归纳新方法、培养数学能力和创新思维的金钥匙。

猜想：an=2n-1,Sn=n2。可用数学归纳法证明此猜想的正确（证明略）。从特殊到一般也符合人类的认知规律，合情推理和演绎推理在这儿相得益彰、各领风骚。

数学教育家弗赖登塔尔认为，学习数学归纳法的正确途径是向学生提出一些必须用数学归纳法才能解决的问题，迫使他们直观地去使用这个方法。在学生发现和懂得了这个方法后，再去帮助他们用抽象形式把它叙述出来。数学归纳法的教学不简单，需要师生的默契配合，需要师生数学素养的提高，需要学生思维能力的有效训练，数学教学也需要时间，静待花开。